Analysis of Tip/Tilt Compensation of Beam Wandering for Space Laser Communication

Our simulation utilizes the infrastructure of the GEOL SLR station. We employ a 1m telescope and use a laser with a signal wavelength of λ = 1,550 nm for laser communication. Additionally, we introduce a beacon beam to measure atmospheric effects, assuming that it resolves the isoplanatism angle issue resulting from different propagation paths compared to the signal beam, as seen in conventional applications such as laser guide stars. Table 1 provides details of the parameters for the proposed system.

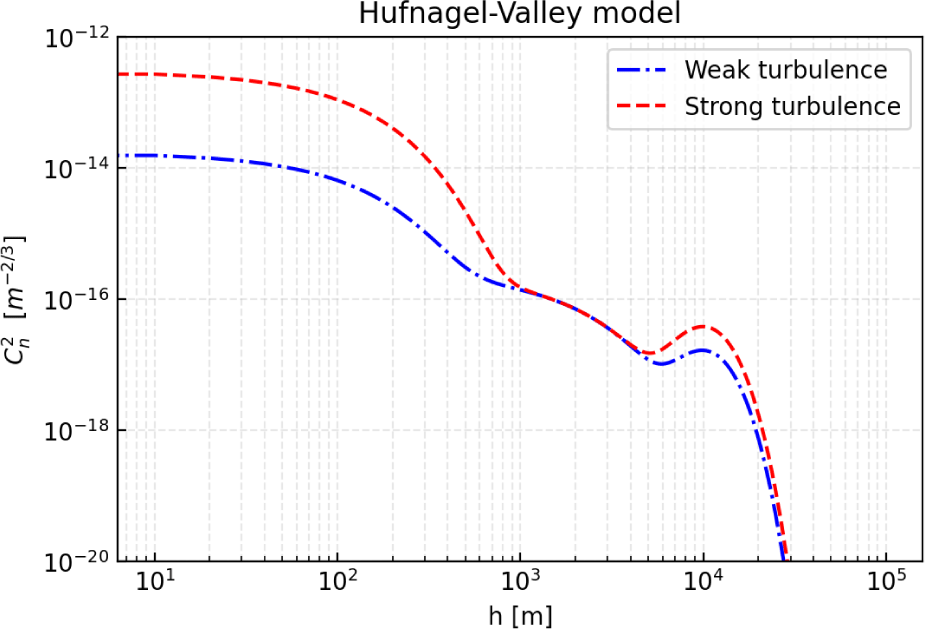
Due to temperature gradients in the atmosphere, turbulent spatial fluctuations cause refraction of the laser propagation direction, simultaneously affecting the wavefront phase. The refractive index structure parameter, known as $C_n^2$, characterizes the refractivity of atmospheric turbulence, which is also referred to as optical turbulence. Numerous models for representing this parameter have been developed. In our research, we employ the Hufnagel-Valley (H–V) model, which is expressed as follows (Andrews, 2019):

where w is root-mean-square(rms) wind speed in m/s, A is the nominal value of $C_n^2\left(0\right)$ at the ground in m^–2/3, and h is the height above sea level in m.

As evident from this model, the refractive-index structure profile with respect to altitude is determined by the values of w and A, which can be considered as a measure of turbulence strength. In this paper, we consider the profile known as the H–V_5/7 model (w = 21 m/s, A = 1.7×10^–14m^–2/3) for weak turbulence and substitute w = 32 m/s, A = 3.0×10^–13m^–2/3 into the H–V model for strong turbulence. Fig. 1 depicts the refractive index values at different altitudes calculated based on the conditions determined above for both weak and strong turbulence.

Fig. 1. $C_n^2$ model profiles according to height for each strong (red) and weak (blue) turbulence.

Download Original Figure

The wavefront of the laser beam arriving at the receiver is distorted and refracted due to atmospheric turbulence, ultimately reaching the receiver. This causes the beam’s center to deviate from the on-axis at the receiver’s focal plane, resulting in spot motion. In addition, jitter from both the transmitter (satellite) and the receiver (ground station) contributes to image dancing. These effects are referred to as AoA fluctuations and occur randomly depending on turbulent conditions. The variance of random AoA fluctuations is denoted as $\langle {\beta }_a^2\rangle$ and can be expressed as follows (Andrews & Phillips, 2005):

where ζ is the zenith angle and D is the receiver’s (telescope) aperture diameter.

In this case, the AoA fluctuation results in the displacement from the center at the focal plane. The variance of this displacement is expressed Eq. (3) as rms (Fernandez et al. 2018), and it is known to follow a Rayleigh distribution.

where, f is focal length of the receiver.

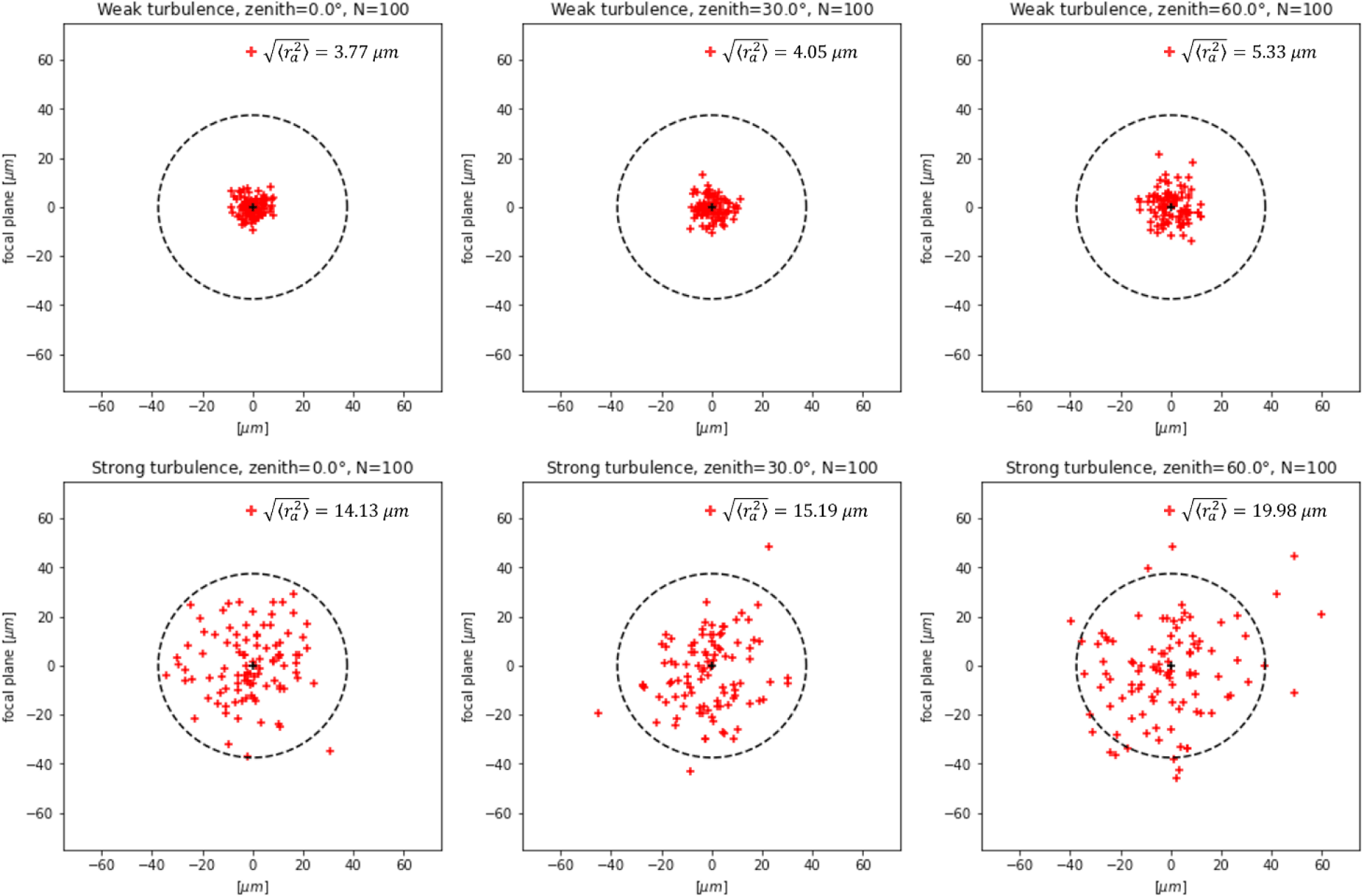
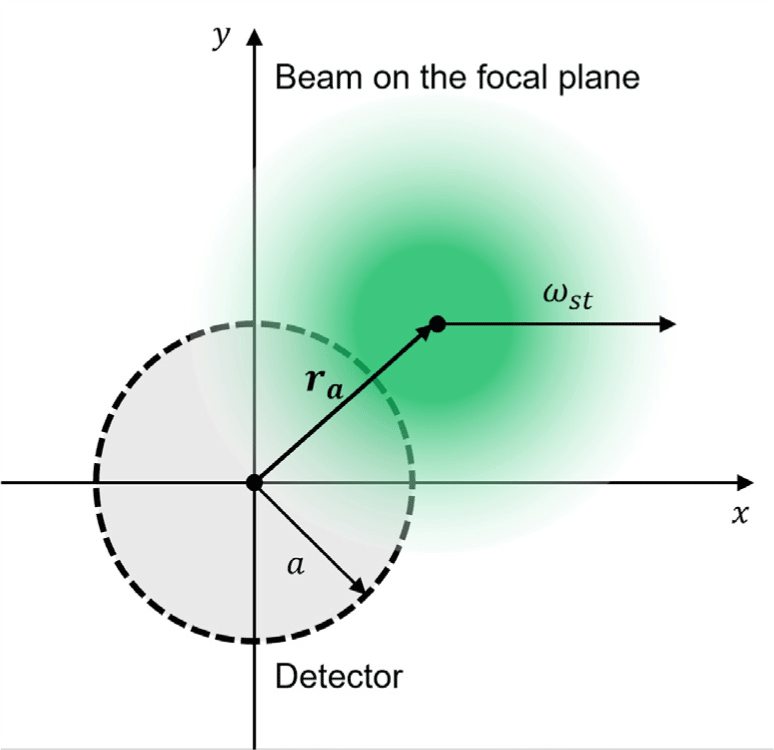
Fig. 2 illustrates how the center of the beam reaches the focal plane due to AoA fluctuations caused by atmospheric turbulence. The dashed black circles in each figure represent the area where the detector detects the beam. In the case of weak turbulence, most of the beam is concentrated within the detector’s area and at its center. In contrast, for strong turbulence, the beam is more dispersed from the center and, in severe cases, it can be observed that it extends beyond the detector’s area. Such errors from the center are one of the factors degrading the power collected by the detector, but they can be compensated for using a tip/tilt mirror.

Fig. 2. The center of the beam reaching the focal plane varies with the zenith angle and the intensity of turbulence. The dashed black circles represent the area detectable by the detector.

Download Original Figure

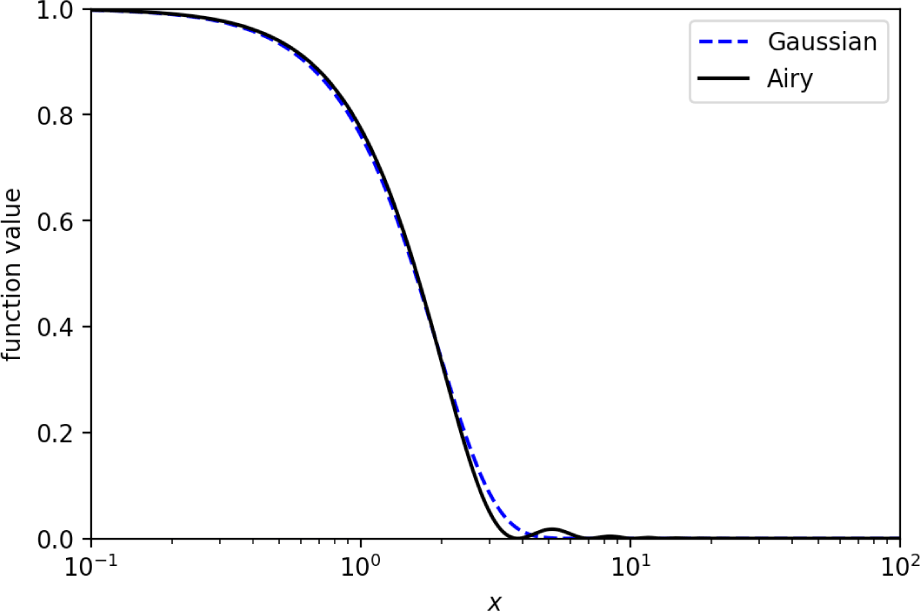
When a beam reaches the focal plane, it is well-known that the intensity of the beam follows a distribution called the Airy disk. As shown in Fig. 2, the center of the beam at the focal plane is offset from the center of the detector. The intensity of the beam that reaches the focal plane forms an Airy disk centered on the beam’s center. As a result, a portion of the beam’s intensity distribution extends beyond the area that the detector can capture. Only the portion of the beam within the detector’s detectable area is received, allowing us to calculate the received beam’s power. For the sake of convenience in our calculations, we approximated the beam’s Airy disk distribution as a Gaussian distribution. The following equation can be used to approximate the Airy function as a Gaussian function (Cheon & Muschinski 2007; Fig. 3):

Fig. 3. Comparison of Airy function (black solid line) and approximated Gaussian function (blue dashed line).

Download Original Figure

where ${𝓙}_1\left(x\right)$ is the first-order Bessel function and x = kRsinθ consisting of the wave number k, the aperture radius R, and the observation angle θ.

Furthermore, when the beam reaches the focal plane, it not only moves away from the center but also experiences spreading of intensity profile from the beam’s center due to diffraction and turbulence. As shown in Fig. 4, atmospheric turbulence exacerbates this spreading, causing the radius of the beam reaching the focal plane to increase further. The full width half maximum (FWHM) of the beam due to diffraction and turbulence is expressed as follows:

Fig. 4. Diagram of diffraction & turbulence -induced beam spreading.

Download Original Figure

The beam’s FWHM due to turbulence is characterized through a metric known as the Fried parameter, denoted as r₀, which represents the optical system’s ability to withstand the influence of atmospheric turbulence to some extent. The FWHM of the beam at the focal plane can be calculated by consolidating Eqs. (5) and (6) as follows (Robbe et al. 1997):

However, in a Gaussian distribution beam profile, the FWHM represents the diameter at which the beam’s intensity becomes 1/2 of its maximum intensity, which does not fully characterize the beam size. The beam radius corresponds to the point where the beam’s intensity drops to 1/e² of its maximum intensity. Using this relationship, we calculate the beam radius as follows:

In this way, we obtain a Gaussian distribution-approximated beam intensity profile through the beam radius, and this in turn allows us to calculate the power of the beam received by the detector. The results of these calculations are presented in Section 3.

Several factors, including atmospheric turbulence-induced AoA fluctuation, contribute to the tilt error (σ_tilt). It can also be calculated through FSM control as follows (Olivier et al. 1993) :

Here, σ_SNR arises due to the finite signal-to-noise ratio (SNR), and σ_TA is induced by finite angular separation between an astronomical object (or guide object) and a reference object, referred to as tilt anisoplanatism. σ_BW represents the error resulting from the finite closed-loop bandwidth of the tip/tilt compensation system while σ_HO denotes the error in the wavefront tilt estimate due to centroid anisoplanatism and uncorrected high-order aberrations expressible by Zernike polynomials. The tilt error before compensation is equivalent to the previously mentioned AoA fluctuation.

Looking at each of the errors, first, σ_SNR can be expressed as follows:

Here, f_c is the tip/tilt system’s closed-loop bandwidth, and f_s is the sampling frequency. f_s should have a value faster than the tilt Greenwood frequency to track AoA fluctuations caused by atmospheric turbulence, and f_c should be at least four times the Greenwood frequency to design an appropriate adaptive optics system (Hemmati 2020).

σ_TA represents the error that occurs when using different optical paths, such as when employing a laser guide star or an astronomical object for atmospheric correction, that are distinct from the signal laser. In this study, using a beacon beam aligns with the same optical path as the signal beam, and therefore, σ_TA is considered to be 0.

σ_BW is the error that arises because the atmosphere changes during the finite time that the FSM’s closed-loop corrects the wavefront tilt induced by the atmosphere. During this time, the object and the reference wavefront tilt change, leading to an error. This error is a dominant factor affecting the tip/tilt adaptive optics system.

Here, f_T represents the tilt Greenwood frequency that describes the minimum closed-loop bandwidth required for tilt compensation, which tracks the changes in tilt due to turbulence in the continuously mixed air, depending on the state of atmospheric turbulence (Tyson 2000). The performance of the closed-loop bandwidth determines the adaptive optics performance for tilt based on how much faster it can move compared to the Greenwood frequency.

Finally, σ_HO arises from high-order aberrations in the wavefront. The wavefront distorted by turbulence includes not only tilt aberration but also all higher-order aberrations. σ_HO represents only the error resulting from the remaining high-order aberrations, excluding tilt aberration.

To correct the σ_HO term, the wavefront distortion caused by turbulence can be analyzed for high-order wavefront aberrations represented in Zernike polynomials using equipment such as Shack-Hartmann sensors. Compensation can be achieved by controlling a deformable mirror. However, we only focus on the effects caused by low-order (tip/tilt), and therefore, we do not consider high-order compensation.

In Table 2, both the uncompensated σ_tilt and the compensated σ_tilt for strong turbulence are presented.

The compensated σ_tilt for each zenith angle decreased approximately by 87% (86.9% in the weak turbulence and by 87.1% in the strong turbulence) compared to before compensation, and the remaining 13% of the compensated σ_tilt appears to be dominated by uncompensated σ_HO. This suggests that to achieve more precise beam center correction, compensation of high-order aberrations is also necessary.

For the convenience of calculation, in Section 2.4, we looked into a method of approximating the intensity of the beam reaching the detector as a Gaussian distribution. If, as shown in Fig. 5, the beam’s center reaches a point r_a away from the center of the detector due to AoA fluctuation, the detector will only capture a portion of the beam. In this case, the collected power of the beam at the detector can be approximated as follows (Yang et al. 2014) :

Fig. 5. The relationship between the beam reaching the focal plane and the detector area, where the gray area represents the detector’s region and the green area represents the Gaussian distribution of the beam at the focal plane.

Download Original Figure

Here, A₀ is the fraction of collected power at r_a = 0 and ω_eq represents the equivalent beam width. The beam’s size is determined by the intensity of turbulence. Depending on the beam’s size, even if the beam’s center reaches beyond the detector, power can still be detected. Conversely, when the beam arrives at the center of the detector (where the detectable power is maximum), any part of the beam extending beyond the detector’s size will result in loss. Such loss cannot be compensated for by tip/tilt alone. In weak turbulence, nearly all of the beam is collected by the detector, while in strong turbulence, the collected beam is significantly reduced, as seen in Fig. 6.

Fig. 6. Variation in the maximum fraction of collected power (A₀) that can be detected by the detector based on the zenith angle. The blue dashdotted line represents weak turbulence and the red dashed line represents strong turbulence.

Download Original Figure

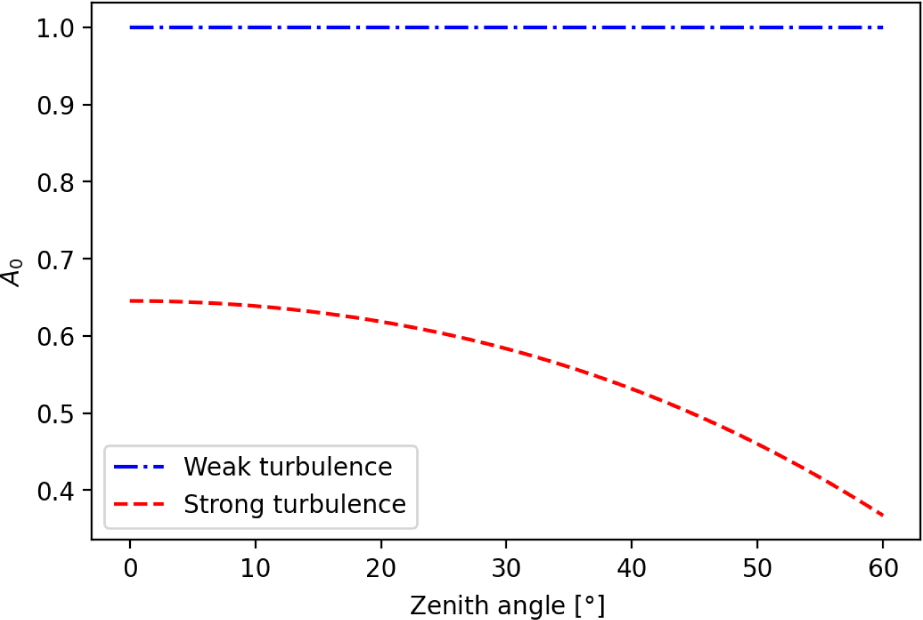
In weak turbulence, since the size of the beam is smaller or similar to the size of the detector, the on-axis beam can be fully collected at the detector. Conversely, in strong turbulence, because the beam’s size exceeds the detector’s size, it is confirmed that a significant portion of the beam entering the detector can be lost even in the absence of pointing error.

Through simulations, we created 1,000 samples for each zenith angle, normalized the ratio of collected beams at the detector, and examined them. Additionally, we compared the collected beams at the detector under reduced tilt error achieved through tip/tilt mirror control. The comparison is presented in Fig. 7.

Fig. 7. The normalized power collected at the detector in strong turbulence. Simulation results before tip/tilt compensation (above) and after compensation (below).

Download Original Figure

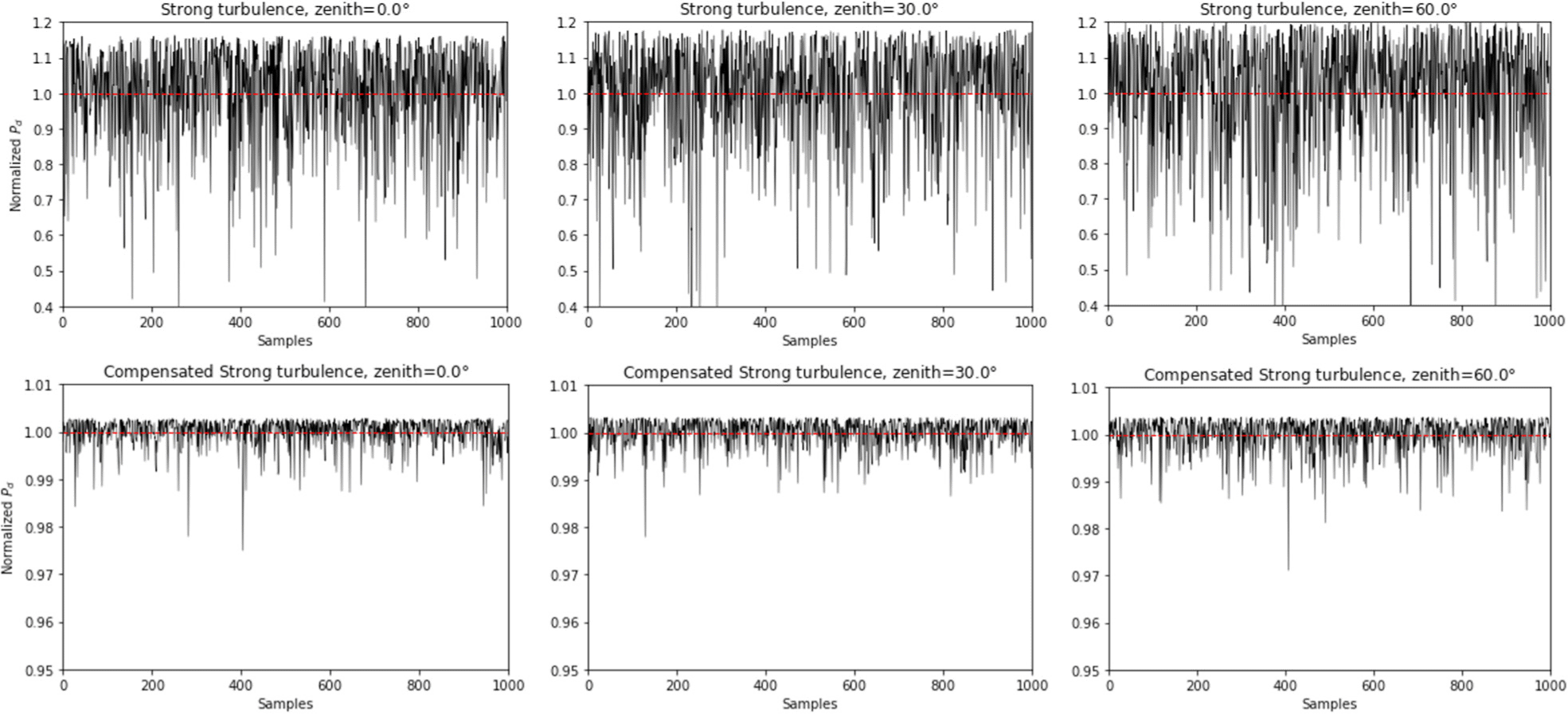
Tip/tilt compensation demonstrates a noticeable reduction in the fluctuation of the collected signal power at the detector. The upper limit of each fluctuation indicates the value of A₀, which is affected by the increased ω_st due to turbulence.

The received power at the detector is determined by the distance between the center of the detector and the center of the beam, r_a, as well as the beam size at the focal plane, ω_st. Moreover, the random distribution of r_a follows a Rayleigh distribution. The probability density function of the Rayleigh distribution is as follows:

where, ${\sigma }_s^2$ is jitter variance at the receiver. The probability density function for the received power P_d at the detector is derived by combining Eqs. (15) and (16) (Farid & Hranilovic 2007).

The collected power is normalized, and the power before and after tip/tilt compensation is compared. In the case of weak turbulence, it was confirmed that even without tip/tilt compensation, most of the beam profiles are already collectable within the detector region. The comparison results for strong turbulence are shown in Fig. 8.

Fig. 8. Comparison of probability density before and after tip/tilt compensation.

Download Original Figure

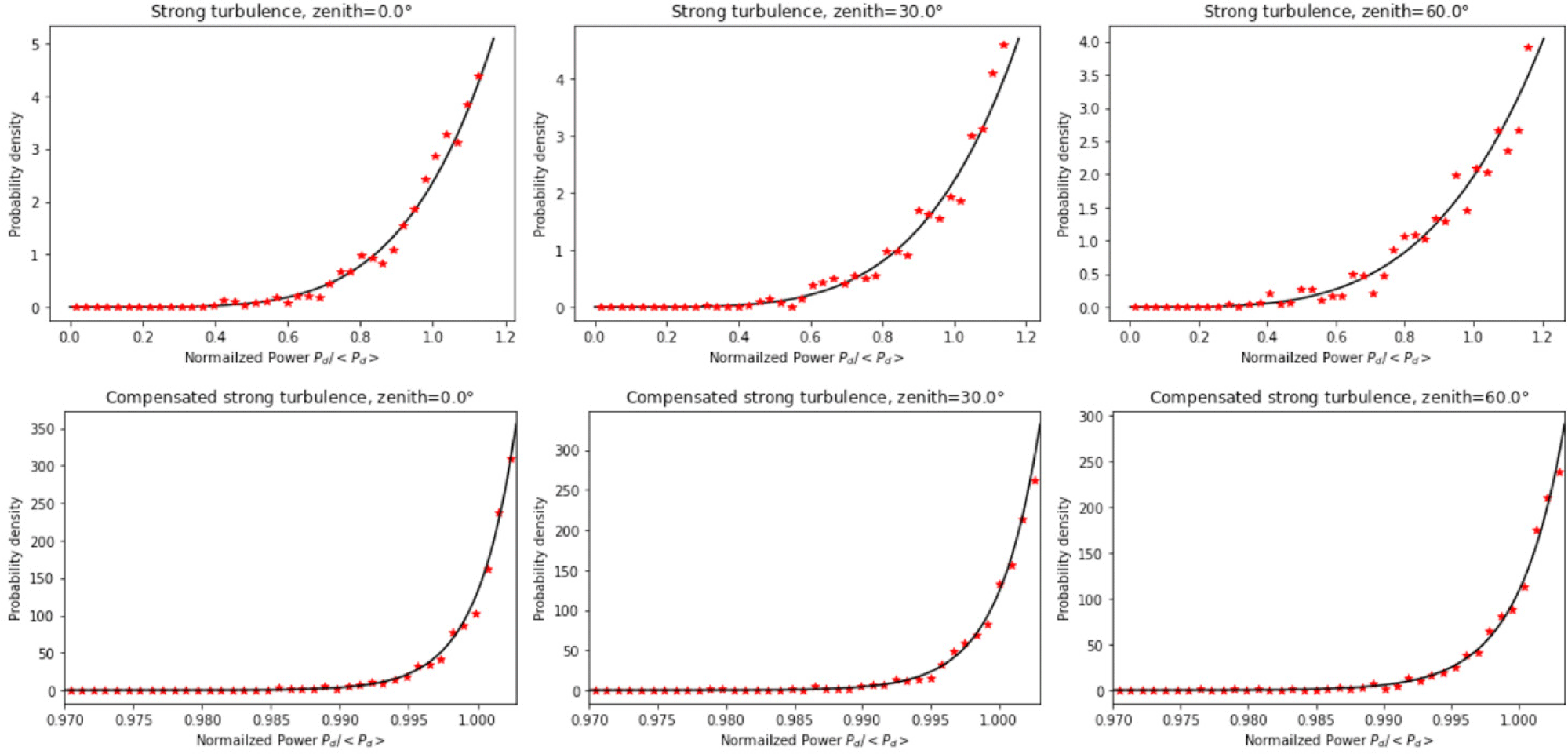
In Fig. 8, the solid black line represents the Rayleigh probability density for normalized power, and the red star-shaped points indicate the distribution from simulated results of normalized power fluctuation. The probability density distribution also confirms that significant reduction in the loss of the collected signal beam at the detector can be achieved through tip/tilt compensation.

The performance of communication is quantified by the BER, which represents the ratio of error bits to the total transmitted bits. The BER depends not only on the modulation scheme used in communication but also on the received signal power. We have confirmed that tip/tilt compensation increases the probability of collecting power at the detector. This increase in received power for the beam can enhance the BER performance in communication systems using modulation schemes like on-off keying (OOK). The formula for calculating the average BER is as follows (Arpali et al. 2008):

where p(u) is the probability density of normalized received power u and erfc(·) is the complementary error function.

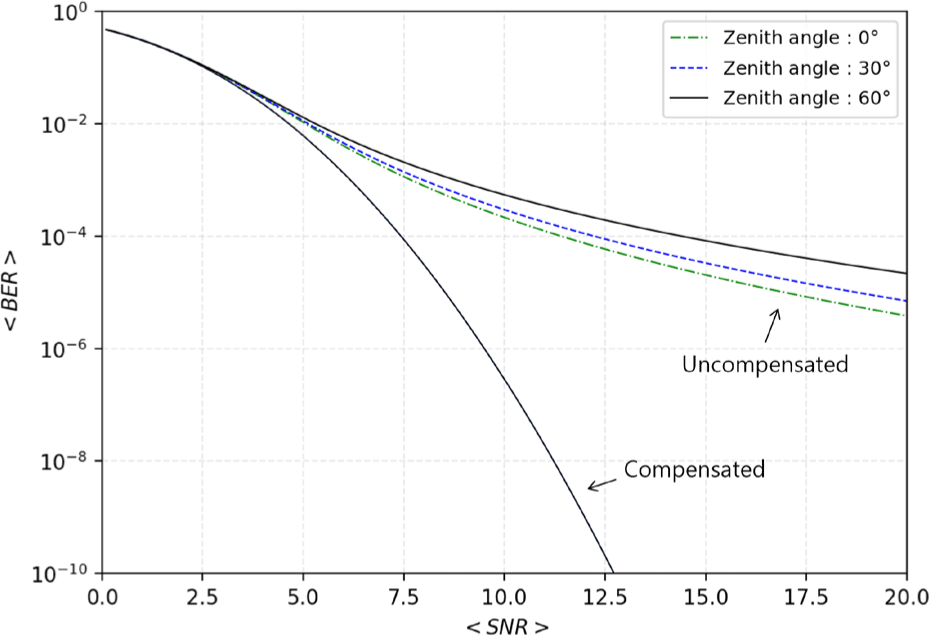
As seen in Fig. 9, it is evident that tip/tilt compensation alone significantly improves the average BER. The uncompensated results show, as expected, that the lower the zenith angle is, the better the average BER is. The compensated results exhibit consistent improvement in terms of average BER regardless of zenith angle variations. This appears to be a limitation of tip/tilt compensation, and to achieve even better results, the correction of factors not considered in this study may be required.

Fig. 9. Comparison of average BER before and after tip/tilt compensation. Green dashdotted line represents ζ = 0°, blue dashed line is ζ = 30°, and black solid line is ζ = 60°. BER, bit error rate.

Download Original Figure