Titius-Bode’s Relation in Exoplanetary Systems

1. INTRODUCTION

Johann Elert Bode published an astronomical compendium in 1772 in which he mentioned a numerical sequence for reproducing the distances of the planets from the Sun in our solar system proposed by Johann Daniel Titius von Wittenberg in 1766. At that time, only the six planets from Mercury to Saturn were known. On triumphant discovery of the planet Uranus by Frederick William Herschel in 1781, Bode recognized that Titius’ relation had correctly predicted the semi-major axis of Uranus and consequently urged his contemporary observers to search for the so-called missing planet at the fifth position between Mars and Jupiter. The subsequent discovery of the dwarf-planet Ceres by Giuseppe Piazzi in 1801, with the semi-major axis predicted by Titius’ relation, made people consider this relation as a natural law and called it the Titius-Bode’s law or Titius-Bode’s rule for some time. The relation was also expected to play a role in exploring the planet Neptune, but its discovery in 1846 was actually led by mathematical calculations for unexpected wobbles in the orbit of Uranus subject to gravitational perturbation by a hypothetical planet.

As it embarrassingly breaks down for objects farther than Neptune, numerous modifications were proposed for the Titius-Bode’s relation (Blagg 1913; Brodetsky 1914; Wylie 1931; Richardson 1945; Dermott 1968; Nieto 1970; Rawal 1978, 1984, 1986, 1989; Basano & Hughes 1979; Louise 1982; Neuhäuser & Freitzinger 1986; Pletser 1986; Ragnarsson 1995; Dermott 1997; Ortiz et al. 2007; Scardigli 2007; Smirnov 2015). Interestingly enough, similar relations can be found for the satellite systems of giant planets in the solar system (Blagg 1913; Brodetsky 1914; Wylie 1931; Miller 1938; Todd 1938; Dermott 1968; Nieto 1970; Rawal 1984, 1986, 1989; Pletser 1986; Stone & Miner 1986; Li et al. 1995). Historical reviews of the Titius-Bode’s relation can be found in Jaki (1972), Nieto (1972), Chapman (2001), and McFadden et al. (1999).

Besides the fact that Neptune’s distance is discrepant, the weakest point of the Titius-Bode’s relation as a physical law is that there is no evidence for the physical basis to explain such a simple mathematical sequence representing the distance of celestial bodies revolving around a central body. Theories of the solar system’s formation have been put forward to account for this kind of distance relation, whose underlying physics to produce an ordered structure includes magneto-convection, plasma turbulence or even self-organizing processes. For example, some ideas involving harmonic resonances between their orbits during planetary system formation have been proposed (e.g., Goldreich & Sciama 1965; Patterson 1987; Filippov 1991). Alternative models utilized the self-gravitational instability in thin Keplerian disks (Ruediger & Tschaepe 1988; Rica 1995), and the principle of least action interaction (Ovenden 1972; Patton 1988). In addition, Hayes & Tremaine (1998) employed physical conditions in the initial proto-planetary disk and concluded that the planets in a stable system are not randomly but regularly spaced. Recently, Laskar & Petit (2017) developed a planet formation model based on an angular-momentum-deficit theory. The question of whether the observed patterns are due to stochastic processes was also attempted (e.g., Lecar 1973; Pletser 1988). It turns out, however, that the estimated probability of chance occurrence is sensitive to the restrictions imposed on the initial orbit environments (e.g., Lynch 2003).

Another critical issue on the Titius-Bode’s relation is if there indeed exists a simple mathematical relation for the distance interval between planets in a planetary system. This question may be tackled by testing whether the Titius-Bode’s relation is valid in exoplanetary systems. If this is the case, it would indirectly demonstrate that the Titius-Bode’s relation is more than a pure mathematical relation. More beneficially, it would be greatly useful to make similar predictions for undetected planets in reported multiple exoplanet systems as the case of the discovery of Ceres (e.g., Mousavi-Sadr et al. 2021). In fact, the Titius-Bode’s relation has been tried for several exoplanetary systems. The exoplanetary system with five planets, 55 Cancri (HD 75732), was investigated with some form of the Titius-Bode’s relation in detail (Chang 2008; Poveda & Lara 2008; Cuntz 2012). Cuntz (2012) claimed that new exoplanet candidates in the 55 Cancri planetary system were predicted through the Titius-Bode’s relation. On the other hand, conclusions remain disputed. For example, Chang (2008) found that the distribution of the exoplanets in the 55 Cnc system is apparently inconsistent with that derived from the Titius-Bode’s relation. Using data from multi-exoplanetary systems, statistical tests have also been attempted to check if the positions of exoplanets obey a simple relation. Chang (2010) statistically explored the distribution of period ratios of exoplanets for 31 multiple exoplanet systems and found that the adherence of the exoplanets to the Titius-Bode’s relation was statistically inconclusive. On the other hand, Lara et al. (2020) used data from 27 exoplanetary systems with at least 5 planets and showed that the planetary orbital periods in exoplanetary systems were not consistent with a random distribution.

This unsettled position to make a conclusion motivates us to revisit the issue of whether exoplanetary systems satisfy the Titius-Bode’s relation with an expanded dataset for improving the statistical significance. Thanks to the space missions such as Kepler and TESS, the number of detected exoplanets has been growing rapidly. As of May 2023, over 5,000 exoplanets have been detected and confirmed. Among these, a total of 856 exoplanetary systems host multiple planets, according to the Extrasolar Planets Encyclopedia (http://exoplanet.eu/catalog). Another merit of the current study is that we can afford to apply the Titius-Bode’s relation separately to the planetary systems whose number of detected planets is different. Thus, we examined planetary systems hosting 5, 6, 7, 8 planets, respectively. In particular, we only focus on the exoplanet systems whose host star is a single star since the Titius-Bode’s relation was originally proposed for the planetary system hosted by a single star. In other words, the exoplanet systems with multiple host-stars might comply with a different rule than the Titius-Bode’s relation, if any. For instance, we exclude the exoplanetary system such as 55 Cancri which is now known as a binary system. Here, as done by Chang (2008, 2010), we investigate the distribution of period ratios of exoplanets detected in 32 multiple exoplanetary systems of a single host star hosting five or more confirmed planets. This paper begins with descriptions of the data of the exoplanetary system that we analyze in this paper in section 2. We present the results of the distribution of period ratios of exoplanets in section 3. Finally, we summarize and conclude our findings in section 4.

2. DATA

The observed parameters for the exoplanetary system are taken from the Extrasolar Planets Encyclopedia and the NASA Exoplanet Archive (https://exoplanetarchive.ipac.caltech.edu/index.html), where recently discovered extrasolar planets are constantly included and updated. In Table 1, we list 32 exoplanetary systems analyzed in this study, in which more than five planets are found to be orbiting around a single host star. In particular, the star KOI-351 (2MASS J18574403+4918185, KIC 11442793, Kepler-90, WISE J185744.03+491818.5) is found to have 8 exoplanets. This star is an F-type star whose effective temperature is ${6080}_{-170}^{+260}$ K, located about 855 pc from Earth in the constellation of Draco. The planet KOI-351 h with a mass of 203 ± 5 M_⊕ is orbiting at the distance of 1.01 AU which is slightly greater than the inner boundary of the habitable zone (http://www.exoplanetkyoto.org/exohtml/KOI-351.html). The star TRAPPIST-1 (2MASS J23062928-0502285) in the constellation Aquarius with the mass of about 0.0898 ± 0.0023 M_⊙ is at the distance of 12.47 pc from Earth and known to have 7 planets, three or four of which are located in the habitable zone (Wilson et al. 2021). Its effective temperature is 2,566 ± 26K, making it the coldest star currently known to host exoplanets. In addition, there are currently 9 and 21 exoplanetary systems hosting 6 and 5 exoplanets by a single star, respectively. Even though there are 5 (1) exoplanetary systems with 5 (6) exoplanets in the triple-star (binary-star) systems, respectively, we only concentrate on the exoplanetary system with a single star as stated above.

3. DISTRIBUTION OF RATIO OF ORBITAL PERIODS

In Fig. 1, we show the distribution of the ratio of the periods for two planets resulting from our solar system and from the Titius-Bode’s relation with 8 terms. It should be stressed that in this study we consider the ratio of the orbital periods of two planets instead of that of the semi-major axes. As long as exoplanetary systems obey the Titius-Bode’s relation, the ratio of the orbiting periods should also satisfy a specific distribution function based on Kepler’s third law. Thus, we deal with a quantity almost independent of mass of the planetary system, since the mass is to be canceled out when taking the ratio. By doing so, one might get rid of an unknown role of mass of the host star in such relation to the distributions of the exoplanet’s spacing. Furthermore, the period of exoplanets is a primary quantity directly measured by observations while the semi-major axis is secondary information deduced with assumptions such as mass.

Fig. 1. Distribution of the period ratios of two planets. In the upper panel, the distribution from our solar system from Mercury to Uranus with Ceres is shown. In the lower panel, the distribution of the ratio of periods of two planets calculated by the Titius-Bode’s relation is shown. To obtain the distribution, we randomly choose two planets and take the ratio of the periods from the outer orbit planet to the inner orbit planet, $\frac{P_{out}}{P_{in}},$ such that the value is always greater than unity.

Download Original Figure

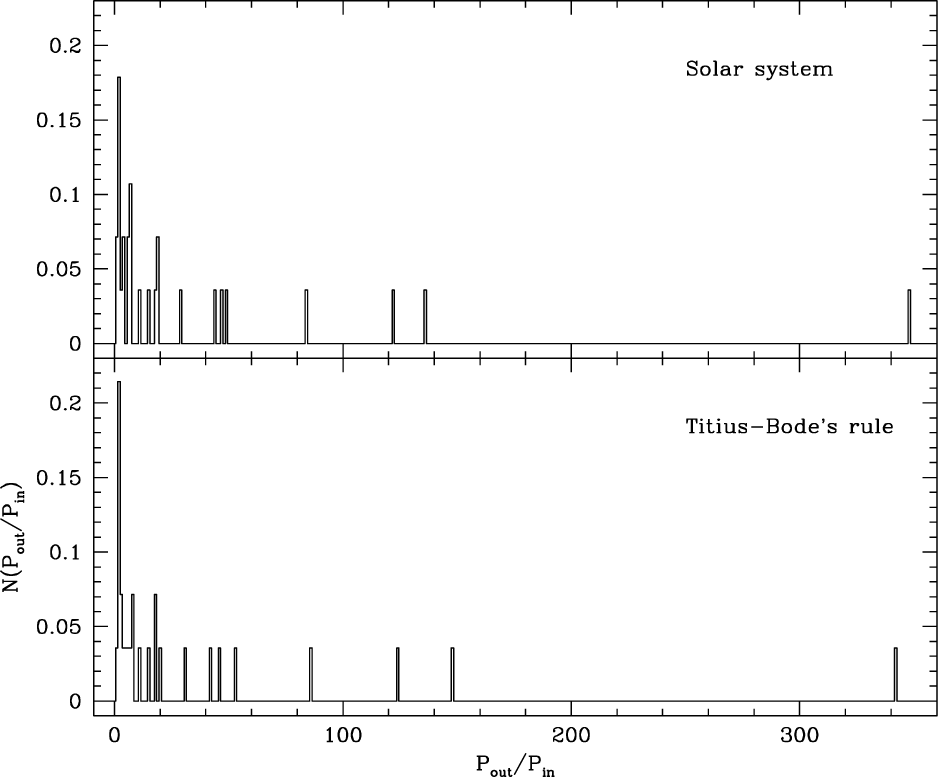
To obtain the distribution, we randomly choose two different planets 10⁶ times securing the statistical significance level and take the ratio in a way that the value is always greater than unity. Even if the classical Titius-Bode’s relation might appear to be an infinite sequence, it is likely to satisfy only a finite number of planets. Moreover, the relation rounded-off at Uranus can be exempted from arguments by perfectionism for a moment in the sense that the planets form in a finite size of the protosolar nebula from which the planets were created after a process of accretion of the planetesimals and the number of planets cannot be infinite. It should be mentioned, however, that the number of planets should not be arbitrary since the condition under which regions of the protoplanetary ring of the particles arose should be subject to chemical composition, shape of protoplanetary systems, and so on. In this context, we have presumed that the Titius-Bode’s relation holds good up to Uranus. We only include planets up to Uranus while Ceres is involved. The Titius-Bode’s relation itself and most of its modifications include Ceres as a representative of a provisional planet in the regular planetary distances. As one may expect, a statistical test by calculating the χ² value demonstrates that the observed ratio distribution is consistent with that derived from the Titius-Bode’s relation. That is, the χ² value is 6.2 with a probability of 96 %, indicating that two data sets are drawn from the same population. Results of the χ² test with different bin sizes also show that they are comparable with high probability of ~90% [see Chang (2010), for test results with different bin size].

In Figs. 2 and 3, we show the distribution of the ratio of periods of two planets resulting from the exoplanetary systems of KOI-351 and TRAPPIST-1, respectively. As for the exoplanetary system of KOI-351, all the planets are distributed inside the orbit of Mars. The semi-major axes of the three planets are less than that of Mercury and the shortest orbiting period is only about a week. Hence, the largest possible ratio of periods of two planets in this system is about 47. On the other hand, for the exoplanetary system of TRAPPIST-1, exoplanets have an orbital period ranging from 1.5 to 19 days, and corresponding semi-major axes are between 0.011 and 0.064 AU. That is, the system is so compact that the distribution of the period ratio is also much narrow. In Fig. 4, the distribution of the ratio of periods resulting from exoplanetary systems hosting 6 exoplanets. Each distribution is also obtained by randomly selecting pairs of exoplanets from all the possible combination in the particular exoplanetary system.

Fig. 2. Distribution of the period ratios of two planets resulting from the KOI-351 exoplanetary system hosting 8 exoplanets.

Download Original Figure

Fig. 3. Distribution of the period ratios of two planets resulting from the TRAPPIST-1 exoplanetary system hosting 7 exoplanets.

Download Original Figure

Fig. 4. Distribution of the period ratios of two planets resulting from the exoplanetary systems hosting 6 exoplanets. The name of the star is indicated in the right upper corner.

Download Original Figure

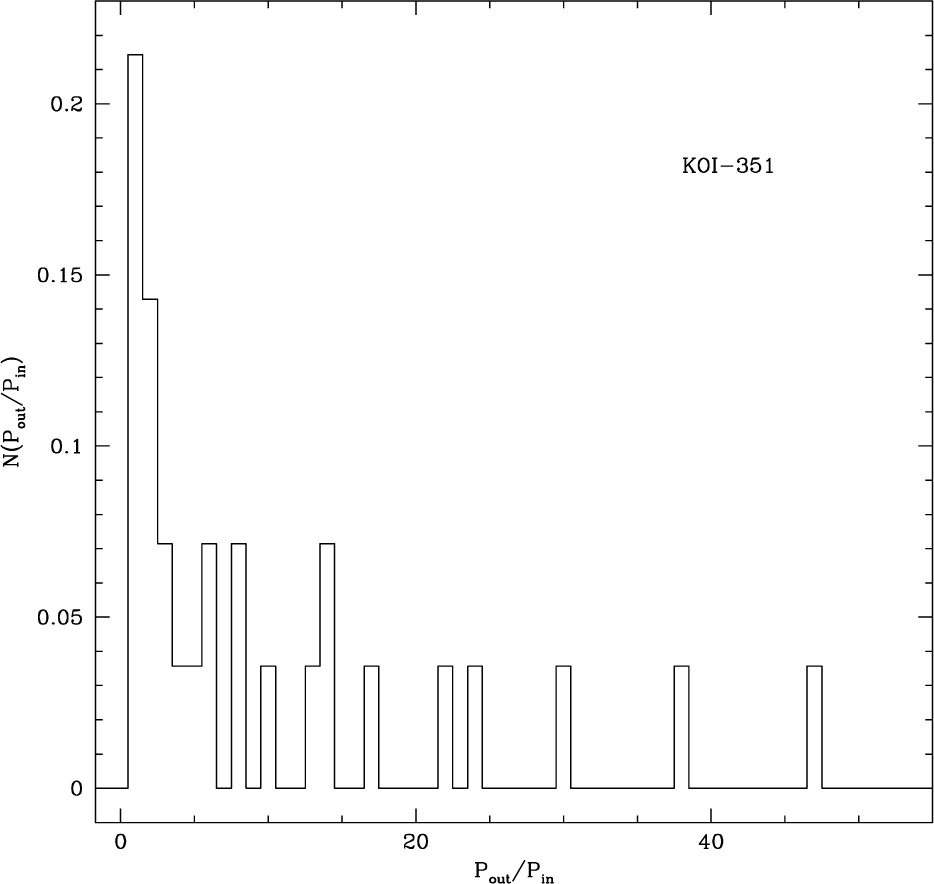
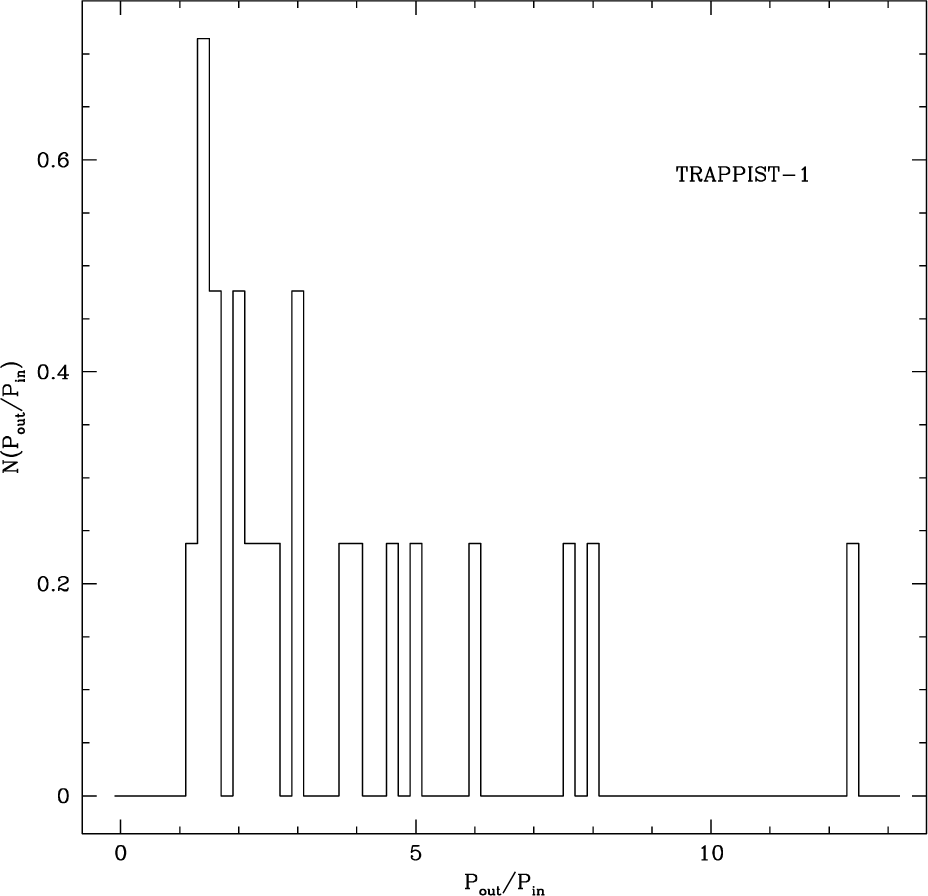
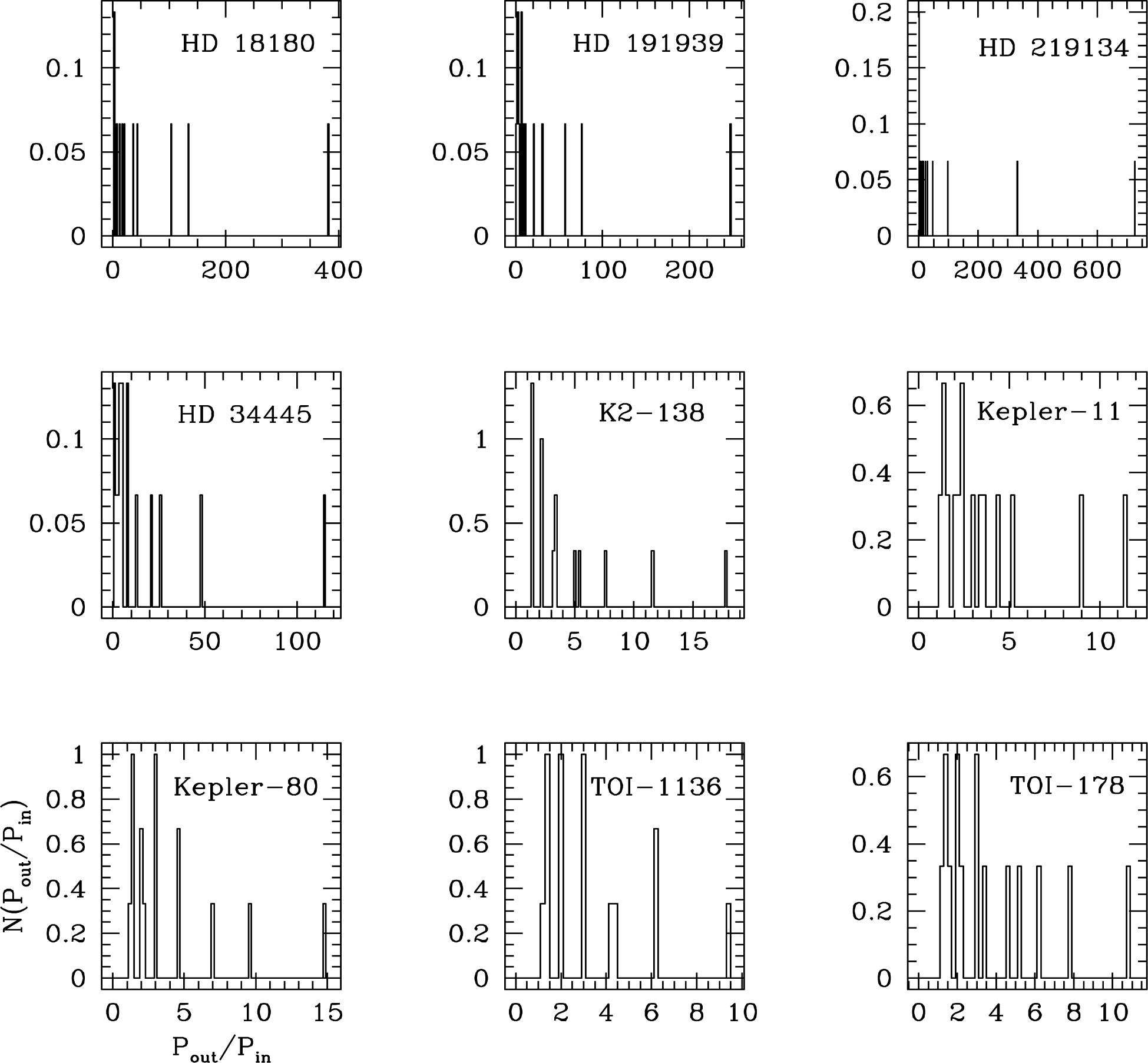
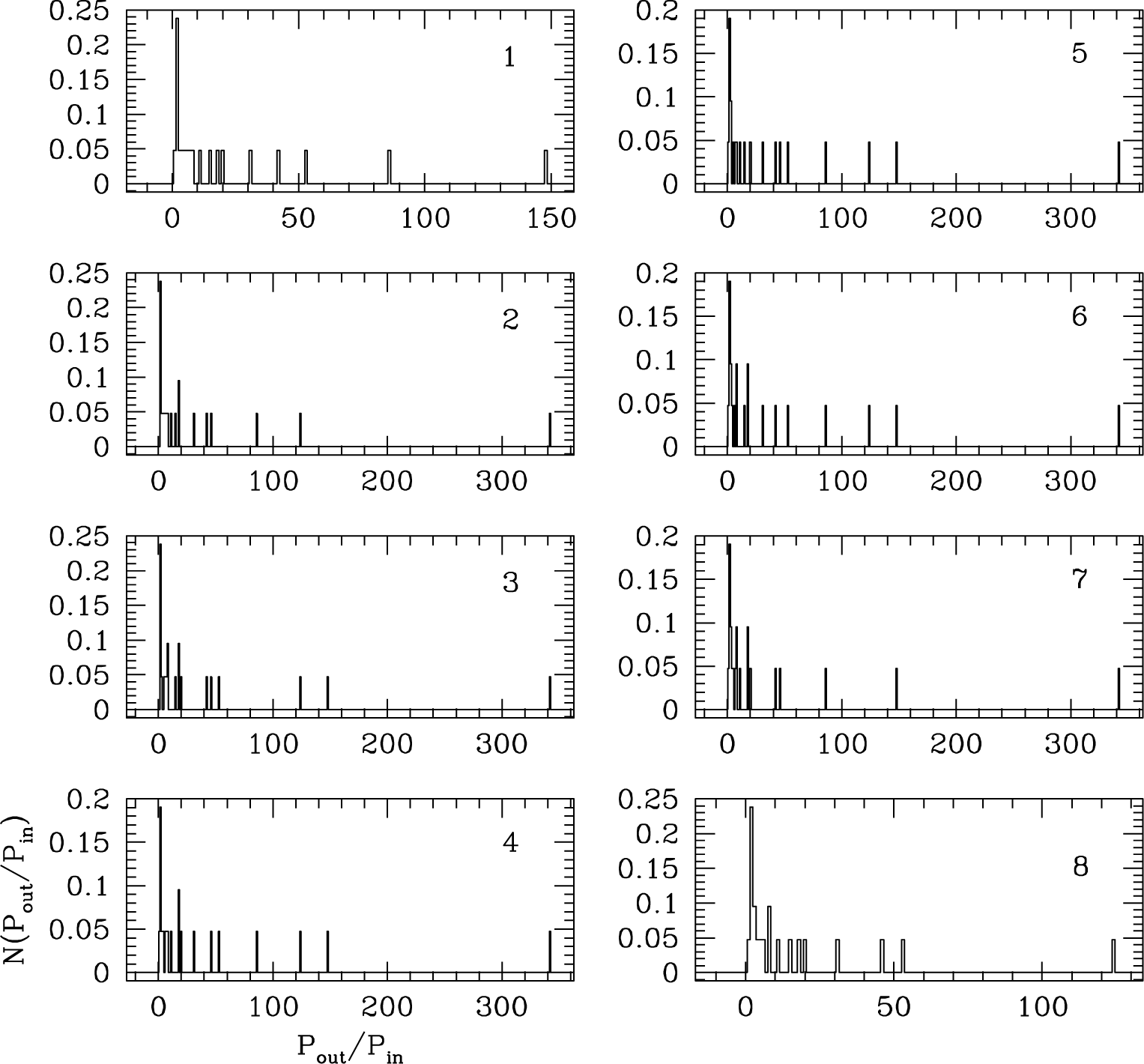
None of the distributions including those from the exoplanetary systems of KOI-351 and TRAPPIST-1 pass the χ² test, demonstrating that none of individual exoplanetary system shown in Figs. 2 to 4 obey the Titius-Bode’s relation. The same conclusion is drawn from the 21 exoplanetary systems with 5 exoplanets, even though resulting distributions have not been explicitly included. It turns out that the resulting probability is less than 50% to indicate that the observed distribution is largely inconsistent with that derived from the Titius-Bode’s relation. To address any potential modification of the distribution due to the selection effect in detecting exoplanets, we repeatedly calculated the distribution of the ratio of periods of two planets from the Titius-Bode’s relation by removing a planet one at a time on purpose. In other words, we simulated the case where only 7 out of 8 planets are observed for some reason. For example, one may imagine the situation where only 7 planets are detected due to an observational restriction although 8 planets are orbiting a host star. The results of the intentional exclusion are 1 of 8 distributions shown in Fig. 5. Note that these distributions are seemingly similar and yet dissimilar to that shown in the lower panel in Fig. 1. Hence, we tentatively conclude that the traditional Titius-Bode’s relation cannot be applied to exoplanetary systems, even if the detection of exoplanets in a particular exoplanetary system is incomplete.

Fig. 5. Distribution of the period ratios of two planets calculated by the Titius-Bode’s relation. We show the case where only 7 planets are selected and 1 planet is omitted on purpose. The number in each panel indicated the ascending order of the removed exoplanet in distance from the closest to the host star.

Download Original Figure

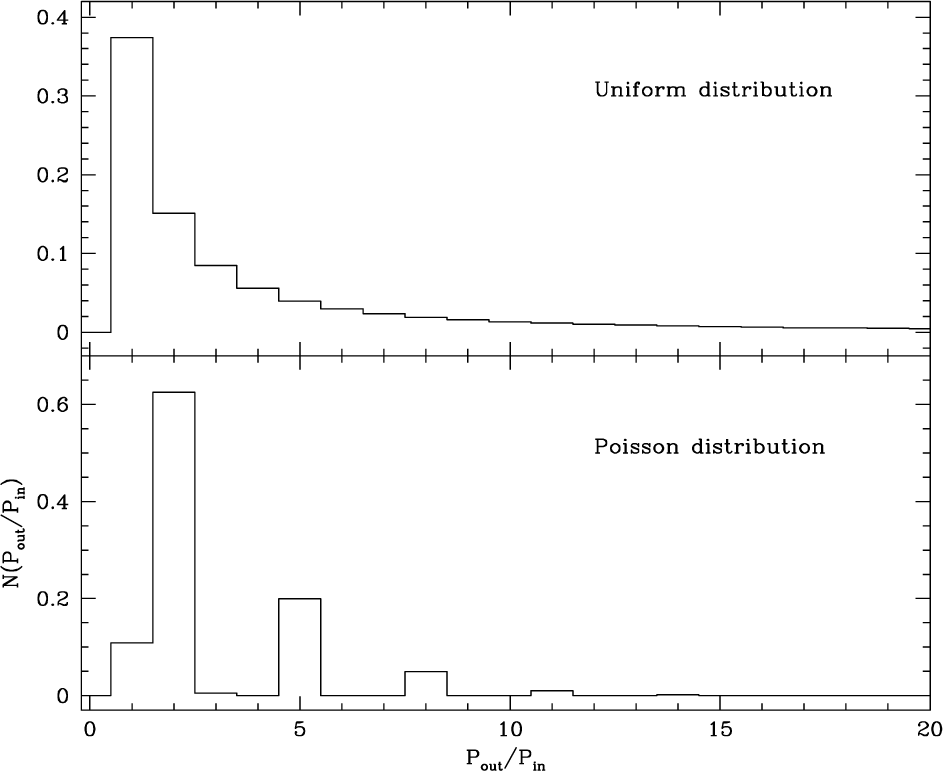
For comparison, we show the distribution of the ratio of periods of two planets derived from an artificial planetary system, whose semi-major axis is distributed by the uniform distribution and the Poisson’s distribution in Fig. 6, respectively. Our artificial exoplanetary system has 8 planets. To generate the distribution function we generated 10⁶ pairs and the bin size in this particular example is unity. Surprisingly, they appear less inconsistent to the observations than the Titius-Bode’s relation does. However, results of the χ² test suggest that the distributions are unacceptable and dependent on how the test was performed. As a result, one has to rule out the possibility that the distribution of the ratio of the orbiting periods in multiple exoplanet systems is consistent with that derived from the uniform distribution nor the Poisson’s distribution.

Fig. 6. Distribution of the period ratios of two planets in an artificial planetary system. In the upper and lower panels, we show results from the uniform distribution of the semi-major axis and the Poisson’s distribution, respectively.

Download Original Figure

4. SUMMARY AND CONCLUSION

Since the discovery of Ceres the curious Titius-Bode’s relation has been studied in terms of the physics responsible for this mathematical sequence or the possibility of using as a useful tool for detecting undiscovered celestial bodies. The question we attempted to tackle in this study is if the Titius-Bode’s relation is valid universally in exoplanetary systems hosting multiple exoplanets. The answer to this question is important partly because the underlying physics is still under debate and partly because it could greatly help to find out small terrestrial exoplanets in multiple exoplanetary systems or exomoons around exoplanets that would otherwise require hard work in observations and data analysis. In this paper, we have examined whether the Titius-Bode’s relation is applicable to exoplanetary systems hosting at least 5 exoplanets. For this purpose, we statistically studied the distribution of the orbiting period ratios of two exoplanets. We considered that taking the ratio of the orbiting period has an advantage since the ratio is independent of the mass of the host star.

We find that the distribution of the ratio of the periods of two exoplanets is apparently inconsistent with that derived from the Titius-Bode’s relation. As a result of the χ² test we carried out, the possibility that the distribution of the ratio of the orbiting periods in multiple exoplanet systems is compatible with that derived from the Titius-Bode’s relation should be ruled out. We interpret this conclusion such that the Titius-Bode’s relation cannot be used to quantitatively assess the possible existence of missing exoplanets in a multiple exoplanetary systems. Having speculated the uniform distribution and the Poisson’s distribution of exoplanets, we tentatively conclude that the distance distribution in exoplanetary systems is also unlikely following those distributions. More rigorous statistical tests should be carried out in terms of the properties of parameters generating sub-samples.