1. INTRODUCTION
South Korea is facing an increasing missile threat from North Korea, including nuclear missiles and weapons of mass destruction. Moreover, North Korea is continuing to develop ballistic missiles and has changed its missile propulsion system from liquid fuel to solid fuel. As a result, the preparation time for North Korea’s missile launches has been reduced. Hence, it is becoming increasingly difficult to identify signs and threats of North Korean missile provocations in advance using South Korea’s current surveillance and reconnaissance assets. Accordingly, South Korea needs to expand its surveillance and reconnaissance capabilities to respond effectively to North Korea’s increasingly sophisticated missile threats. In particular, there is an urgent need to secure military surveillance and reconnaissance satellites in the space domain (Ko 2021).
The purposes of using satellite images are different in military and civilian applications. Moreover, civilian Earth observation satellites and military reconnaissance satellites have different requirements in terms of operating orbit, revisiting frequency, and image quality. In the private sector, satellite images are used for map production, environment and resource monitoring, and national land management. Therefore, image information is collected for a wide range of observation targets. In comparison, military reconnaissance satellites are required to observe specific movements of the enemy at specific times because the military needs to collect image information on major facilities or critical targets of the enemy. Due to these differences in purpose, the collection of satellite image information at the level required by the military using only private satellites is inevitably limited.
Currently, the Republic of Korean military is pursuing a project to secure its first military reconnaissance satellite. In the future, they will secure additional military reconnaissance satellites as the enemy threat increases and are expected to steadily improve their image information collection capabilities by improving the performance of observation satellites. In particular, it will be essential to employ high-resolution satellites that are capable of observing and analyzing key targets.
Cameras mounted on satellites to observe objects on the ground were developed remarkably as they began to be used as tools for advanced intelligence warfare between the United States and the former Soviet Union during the Cold War. Since the late 1990s, advanced countries in satellite technology (including the United States) have been attempting to acquire high-resolution observation images by operating satellites equipped with large optical systems in low orbit (Kim 2013).
There are two methods for acquiring high-resolution images through the use of satellites. The first is to mount a large optical system on the satellite. Examining these satellites more closely, the Hubble Telescope was developed for the purpose of astronomical observation. It is a super-large satellite with a weight of more than 10 tons, a length of 13 m, and a main reflector of diameter of 2.4 m. Another example is Keyhole-11, which is a well-known optical spy satellite of the United States. This satellite weighs 13–20 tons, is 20 m long, has a 2.4 m reflector, and has a theoretical resolution of 15 cm. However, such super-large satellites incur significant costs in terms of manufacturing, testing, and launching (Wikipedia 2005; Kim 2013).
Another way of acquiring high-resolution images is to reduce the satellite’s operating altitude. For example, if a low orbit observation satellite (500–600 km) is operated at lower altitudes (250–350 km), the observation accuracy can be dramatically improved using the same optical system. Very low altitude satellites are equipped with low-cost, small optics and can achieve the same level of observation precision as satellites with large optics in high orbit. Accordingly, active research and development are being conducted on very low altitude observation satellites. For example, Ceccanti & Marcuccio set up a Sun-synchronous orbit with a perigee altitude of 220 km and an apogee altitude of 296 km. They also proposed the concept of using an electric thruster to maintain the designed argument of perigee and eccentricity. Ultimately, their analysis of the results indicated that using electric thrusters would require approximately 45 kg of thrust fuel for a 2.5-year mission (Ceccanti & Marcuccio 2003). Similarly, to monitor North Korea more precisely from very low altitudes, South Korea is also designing a micro-satellite that can perform video recording and transmission missions while maintaining orbit with an electric thruster, which involves developing related core technologies (Yoon et al. 2021). Aguttes et al. (2005), Crisp et al. (2020), and Llop et al. (2014) described the advantages and potential applications of low altitude observation missions with elliptical orbits compared to circular orbits.
The aim of this study was to design an elliptical orbit for precise observation of a specific observation area at a low altitude. For this purpose, critical inclination with no change in the argument of perigee was set as the inclination of the orbit, and Sun-synchronous characteristics suitable for optical observation were applied. Accordingly, in this paper, we propose an orbit that can acquire high-resolution images through low altitude observation in the Korean Peninsula region by using existing small observation satellites without any design changes.
The remainder of this study is organized as follows. Section 2 describes the relationship between satellite Earth observation resolution and orbit altitude. We compared the advantages and disadvantages of circular and elliptical orbits for implementing low altitude observation satellite orbit. In Section 3, we identified that the critical inclination orbit could be advantageous for specific region observations. In Section 4, critical inclination orbit with Sun-synchronous characteristics is derived for electro-optical (EO) Earth observation. Finally, Section 5 provides a conclusion and discussions for further study.
2. RESOLUTION OF EARTH OBSERVATION ORBIT
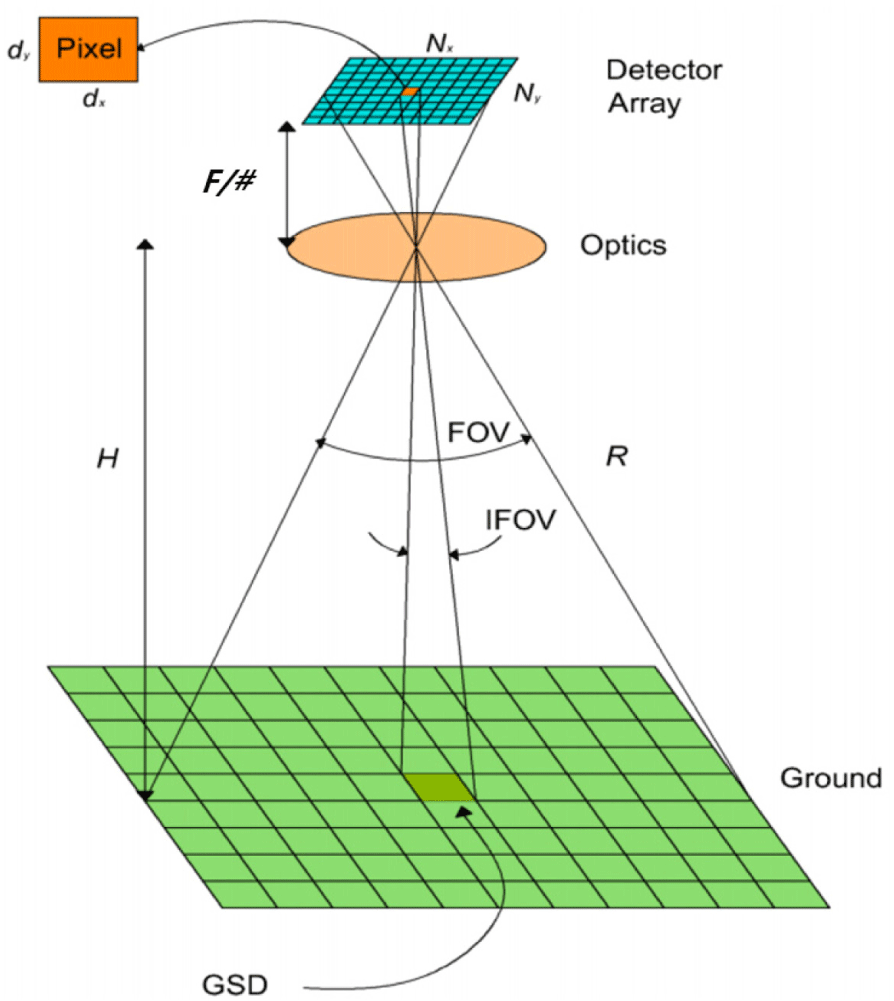
In the context of Earth observation, spatial resolution is defined as the ground sample distance (GSD), which is related to the number of pixels of the camera used to reproduce the image (Wertz 1999). In other words, the more pixels that are used, the better the image quality. A GSD is a geometric projection of a single pixel onto the ground (Fig. 1), and is mathematically defined as follows:
where d is the pixel size (mm), H is the satellite altitude (m), and F is the focal length (mm).
As shown in Eq. (1), GSD is determined by three factors: pixel size, satellite altitude, and focal length. Pixel size and focal length depend on the EO observation payload design. Pixel size is determined by the selected charge-coupled device (CCD) sensor, and the focal length is determined by the size of the EO camera. This indicates that longer focal lengths require larger optical apertures and larger spacecraft buses. Table 1 lists examples of Korea’s high-resolution Earth observation satellites, from which it can be observed that the higher the resolution, the larger the size and mass of the satellite.
It is known that Keyhole (a representative large US satellite) has an optical size of 2.5 m and a GSD of 6.0 cm at an altitude of approximately 250 km. However, significantly high costs are incurred when developing and manufacturing such large satellites ($1.75 billion in 1990). In addition, extensive quantities of thrust fuel are required to maintain satellites with large optical systems at low altitudes (Wikipedia 2005). Table 2 displays the satellite and orbital characteristics developed through the Keyhole Project in the United States. Similar to the US Keyhole Project, Russia has also developed a reconnaissance satellite with a resolution of several tens of centimeters, called the Yantar Project, which uses the same technique of a low altitude orbit (Wade 2019).
Instead of developing large satellites to obtain high-resolution images, a more cost-effective approach is to lower the satellite’s altitude. Therefore, this paper focuses on improving satellite GSD by lowering the satellite altitude while utilizing EO payloads that have already been designed, implemented, and tested in orbit.
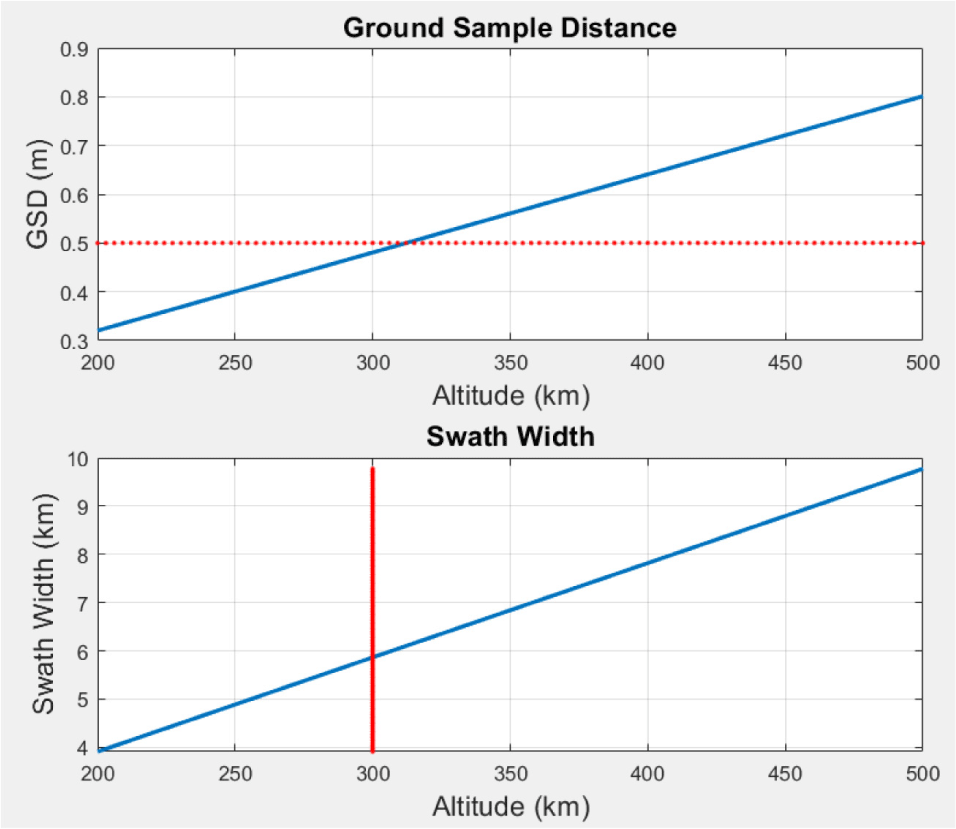
A recently-developed CCD image sensor has a pixel size of 7 µm and over 12,000 pixels (Teledyne 2022). When using this sensor and an optical payload (SaTReC 2008) with an observation angle of approximately 1.12° (optical aperture = 0.3 m), which has already been developed in small satellites, the GSD and swath width according to altitude can be predicted, as shown in Fig. 2.
From the analysis results in Fig. 2, it is evident that if the observation operating altitude of the satellite is reduced, an observation resolution with a GSD of 0.5 m can be obtained by using a small observation satellite. This means it is possible to obtain the same observation resolution of a medium-large satellite using a small observation satellite while employing the existing optical observation satellite technology unchanged. If a satellite is operated in low orbit, it would have the following advantages (Crisp et al. 2021).
First, lowering the altitude of the optical system increases image resolution. Accordingly, the size and weight of the optical system can be reduced. Second, by reducing the distance to the target (or the ground), the signal-to-noise ratio is improved, increasing radiometric performance. Third, at low altitudes, mapping errors due to attitude determination and pointing accuracy are reduced, improving the geospatial accuracy of terrestrial imagery and location-based services.
3. VERY LOW ALTITUDE ORBIT
As mentioned previously, if the operating altitude of a satellite is lowered, its observation resolution can be further improved. However, in a circular orbit, as the operating altitude of a satellite decreases, atmospheric drag increases, making it difficult to maintain the orbit. The drag acceleration that a satellite experiences due to atmospheric drag is expressed as follows (Vallado 2013):
where A is the area of the satellite subject to atmospheric resistance, m is the mass of the satellite, CD is the atmospheric drag coefficient of the satellite (usually 2.2), v is the relative velocity between the atmosphere and the satellite, and ρ is atmospheric density.
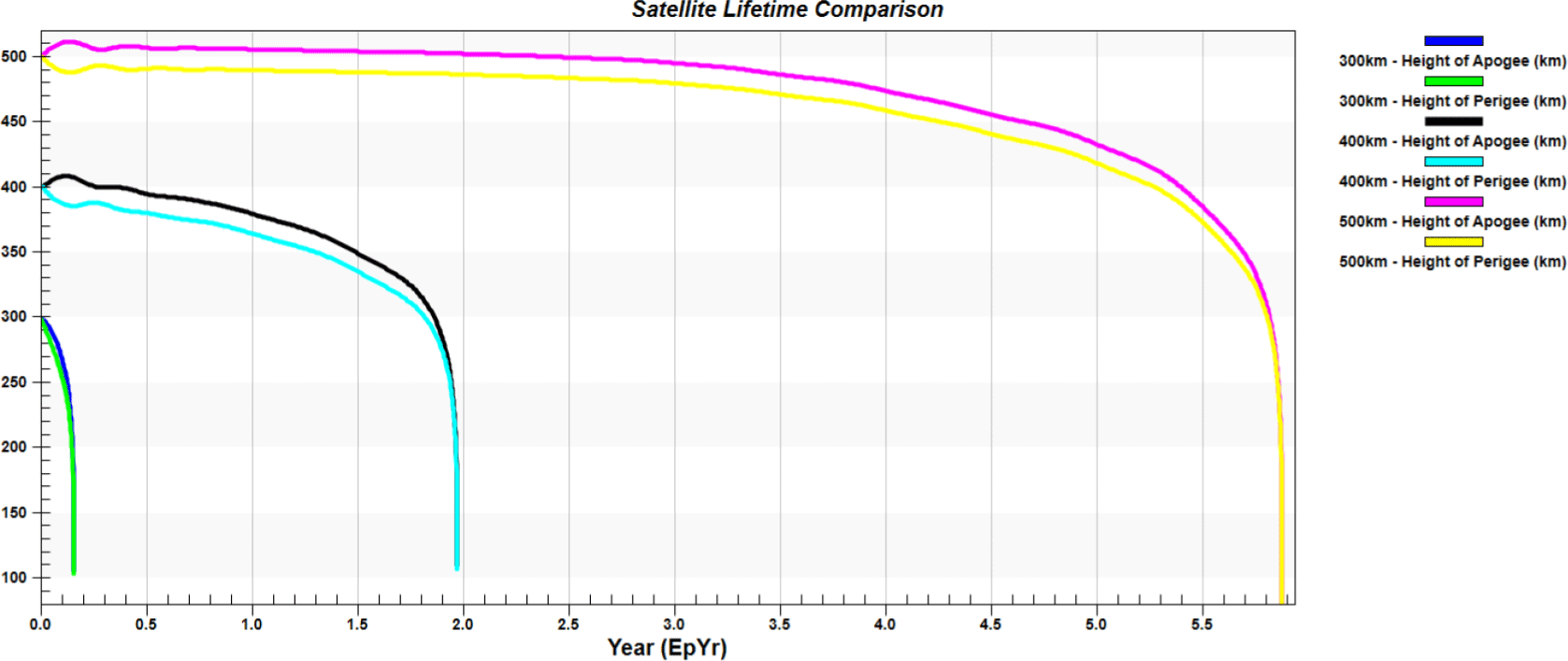
There is a range of atmospheric density models, including the exponential atmospheric model, the Jacchia-Roberts (1971) Model, the Jacchia-Bowman (2008) Model, and the NRLMSSE-00 Model. These models predict atmospheric density by considering the satellite’s operating time, altitude, position (latitude and longitude), F107 Solar Flux, and Earth’s magnetic index. Fig. 3 presents the results of calculating the lifetime of circular orbits at altitudes of 300, 400, and 500 km by applying the NRLMSISE-00 density model to a satellite with an area of 1 m2 and a mass of 100 kg.
Based on the results of Figs. 2 and 3, it is evident that a low altitude (300 km) small satellite for obtaining a high observation resolution of 0.5 m decays within approximately 58 days if a thruster is not used. To compensate for these disadvantages, a thruster must be periodically used to maintain the altitude of the satellite. Ceccanti & Marcuccio (2003) proposed a method to compensate for the altitude drop by using approximately 50 g of xenon fuel per day to maintain an operating altitude of 220 km at perigee and 296 km at apogee altitude for a satellite with a maximum weight of 500 kg, equating to approximately 45 kg for up to 2.5 years. Similarly, Yoon et al. (2021) proposed a circular orbit Earth observation satellite that uses xenon based electric propulsion system to maintain its operating altitude of 300 km.
Recently, the technology trend of small Earth observation satellites has developed to the extent that Earth observation resolutions of less than 1.0 m can be obtained at an altitude of 500 km with satellites weighing less than 100 kg (SaTReC 2022). In this study, a very low altitude operating orbit was applied to improve observation resolution in a specific area (Korean Peninsula) by using a satellite payload of the same class. However, as evidenced by the orbit life prediction results in Fig. 3, the orbit life would be very short if the satellite were operated in a low altitude circular orbit. To address these disadvantages, as shown in Table 3, a method using an elliptical orbit with a low altitude of perigee and a high altitude of apogee can be applied. Table 3 lists the results of predicting the change (decrease) of the semi-major axis for circular and elliptical orbits capable of low altitude observation (Aguttes et al. 2005).
As shown in Table 3, the decay rate in the semi-major axis of a circular orbit during one day is relatively greater than that of an elliptical orbit with the same altitude at perigee. Even in the case of an elliptical orbit, the lower the altitude of perigee, the greater the orbital decay rate. In this study, by considering the observation resolution according to the altitude in Fig. 3 and the orbital decay rate in Table 3, we determined that using an elliptical orbit with an altitude of approximately 300 km at the perigee would improve observation resolution when using a small satellite. However, for an elliptical orbit, the argument of perigee changes, as shown in Eq. (3), by the J2 perturbation of the Earth’s gravitational field:
where a is semi-major axis (km), e is eccentricity, i is inclination (rad), J2 is the zonal harmonic of the second order, Re is the Earth’s average radius (km), and n is the satellite’s average angular rate (rad/s).
For example, if the argument of perigee is set to the latitude position of the Korean Peninsula in an elliptical orbit of 300 × 8,500 km and orbit propagation is performed, the latitude of perigee changes according to Eq. (3). In this study, since the high-resolution observation area is limited to the Korean Peninsula, such changes should not exist or be minimized. Therefore, it is necessary to design an elliptical orbit in which the perigee is maintained in the Korean Peninsula, meaning the argument of perigee does not change. One method of achieving this is the critical inclination orbit proposed by Liu (2011). For this orbit, the inclination angle of the elliptical orbit is set as follows to minimize the change in the argument of the perigee in Eq. (3):
Fig. 4 presents the result of a comparative analysis of the change in the declination of the perigee when the orbital inclination angles are set to 43.0° and 63.435° in an elliptical orbit with a perigee altitude of 300 km and an apogee altitude of 8,500 km. As shown in Fig. 4, when the orbital inclination angle was set to the critical inclination orbit condition, there was barely any change in argument of perigee. This means that the orbit can be designed to ensure that the perigee of the elliptical orbit remains at a specific location on the ground. Based on these results, we planned to design an orbit that always maintained the perigee in the Korean Peninsula.
4. CRITICAL INCLINATION SUN-SYNCHRONOUS ORBIT
Optical observation satellites must satisfy the Sun-synchronous condition along with the condition that the argument of perigee must remain constant. The Sun-synchronous orbit has the characteristic of securing constant illumination from the Sun, especially in the case of visible light observation. This is achieved by maintaining a constant angle between the orbital plane of the satellite and the line of sight vector of the Sun.
A Sun-synchronous orbit must be designed so that the satellite passes over any given point of the Earth surface at the same local time. The angular velocity of the Sun at the center of the Earth and the angular velocity of the satellite’s ascending node due to J2 perturbation are given by Eqs. (5) and (6):
Therefore, a Sun-synchronous orbit must satisfy the following condition: . The calculation for the inclination angle and eccentricity of an orbit that satisfies these conditions was presented by Aguttes et al. (2004), as follows:
and
The orbit inclination angle of Eq. (7) must have a value of 63.4349° or 116.5651° to satisfy Eq. (4), which is a critical inclination condition. For Eq. (8), the value of 116.5651° should be applied to ensure the inner root term is not negative. Therefore, the values for eccentricity and semi-major axis of the elliptical Sun-synchronous orbit can be obtained using Eqs. (7) or (8) when the desired altitude of the perigee is determined. The altitude of the apogee can be calculated using the altitude of the perigee and the calculated eccentricity.
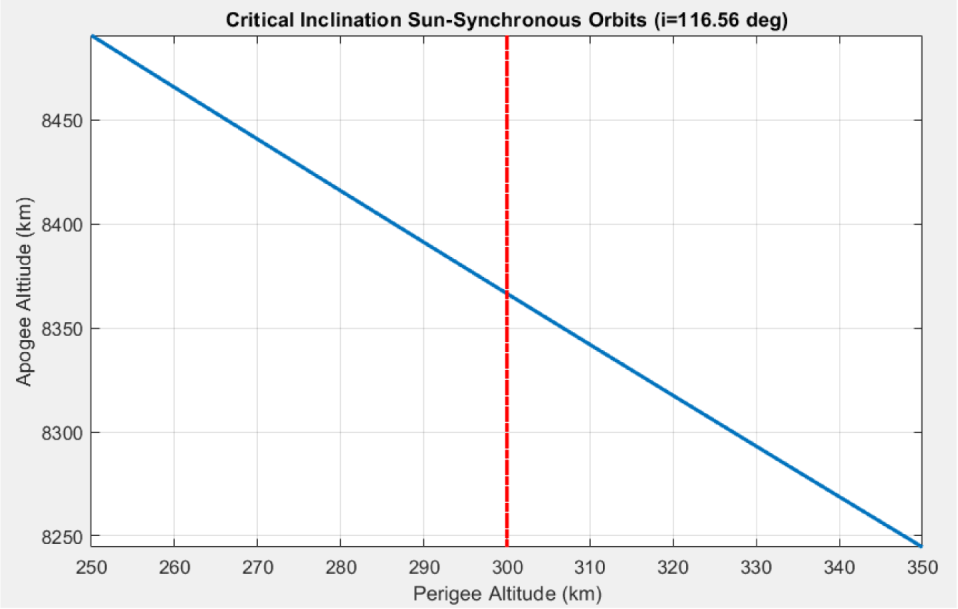
In this study, the altitude of the perigee was set from 250 to 350 km, and the altitude of the apogee satisfying the critical inclination Sun-synchronous condition was calculated. The desired orbits were calculated using Matlab’s fminfunc function after specifying the altitude of perigee. Fig. 5 displays the result of the calculated perigee altitude versus the calculated apogee altitude.
5. RESULTS AND DISCUSSION
Using the critical inclination Sun-synchronous orbit mentioned previously, an orbit capable of high-resolution was designed by lowering the observation altitude of the satellite for the Korean Peninsula region, and its characteristics were analyzed. For the orbit design, the altitude of the perigee was set at 300 km, and it was assumed that the previously secured optical payload and bus technology (SaTReC 2008) could be utilized. As shown in Fig. 2, these observation satellites can achieve an observation resolution of 0.5 m (or less) when the operating altitude is reduced to 300 km. Therefore, a critical inclination Sun-synchronous orbit with a constant argument of perigee could be designed (as shown in Table 4), where the altitude of the perigee is 300 km and the location of the perigee is in the Korean Peninsula.
| Satellite orbit | Designed value |
|---|---|
| Perigee altitude | 300 km |
| Apogee altitude | 8,366.52 km |
| Eccentricity | 0.3765 |
| Inclination | 116.565° |
| Argument of perigee | 45° |
| Right ascension of ascending node | 153° |
The altitude of the perigee, the altitude of the apogee, the eccentricity, and the inclination angle of the orbit design of Table 4 were the values used to satisfy the critical inclination Sun-synchronous condition. The argument of perigee is a value for locating the perigee in the Korean Peninsula. The right ascension of the ascending node was set to ensure that the optical observation satellite could pass the equator at approximately 13:00 local time while maintaining a constant angle between the satellite’s orbital plane and the Sun. Fig. 6 presents the shape of the critical inclination Sun-synchronous orbit designed for precise observation of the Korean Peninsula.

From the left side of Fig. 6, it is evident that the position of the argument of perigee in orbit is located in the Korean Peninsula. Furthermore, the right side of Fig. 6 indicates that the orbit has the shape of an elliptical orbit with relatively large eccentricity. Table 5 presents the result from analyzing the local time at which the satellite passes the ascending node of the orbit, which was designed to have the characteristics of both an elliptical and a Sun-synchronous orbit. In Table 5, the local time and the ascending node (z = 0) were calculated using Eqs. (5)–(7). The results in Table 5 confirmed that the local time at which the satellite passed the ascending node was maintained constant at approximately 13:00.
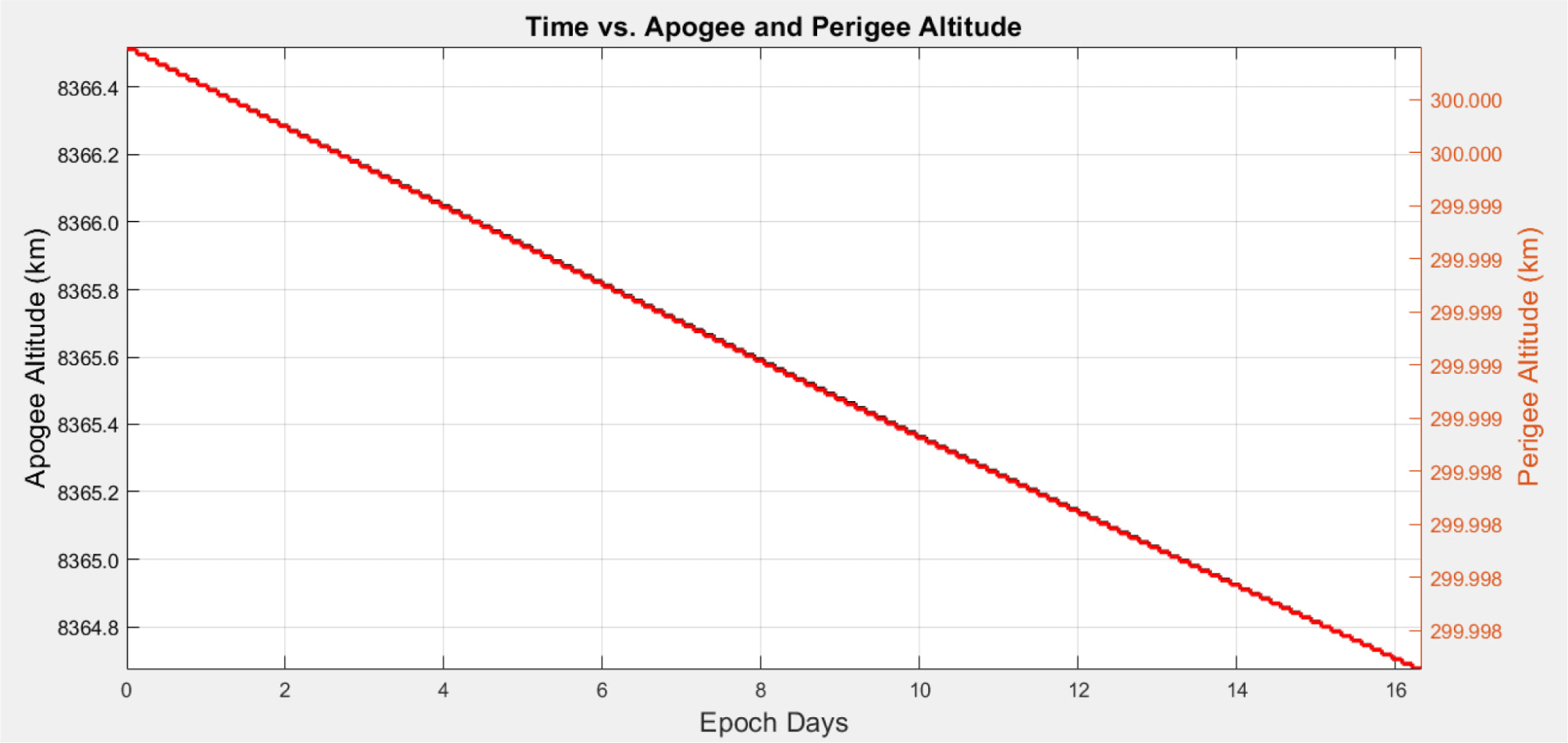
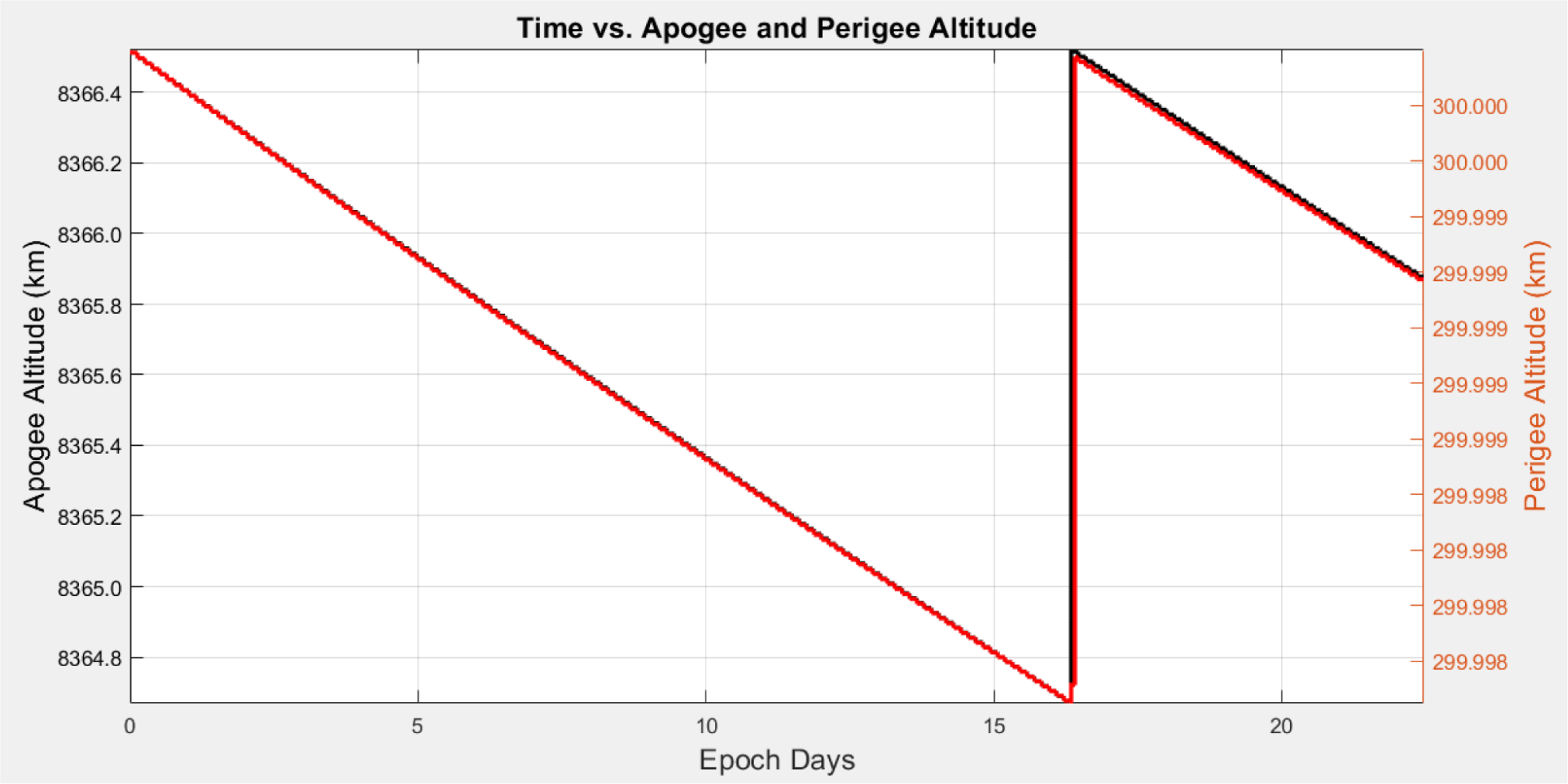
Since the designed orbit was elliptical with a low altitude of perigee, a change in orbit due to relatively large atmospheric resistance could occur when passing through the perigee region. Fig. 7 presents the result of analyzing the decrease in the orbit of perigee and apogee when the orbit was propagated by applying J2 perturbation and atmospheric drag for approximately 16 days. From Fig. 7, it is evident that there was almost no change in the altitude of the perigee, although the altitude of the apogee decreased by approximately 1.5 km. Therefore, given the long mission life of approximately 3 years, a thruster would be required to compensate for this change in altitude.
Fig. 8 presents the analysis result for orbit compensation using a thruster with a thrust of 1 N and a specific impulse of 300 s. The designed orbit had a relatively large eccentricity. Despite the large atmospheric drag due to the low perigee altitude, we confirmed that it did not require much thrust to maintain altitude because it flew at the perigee altitude for a relatively short time. We also confirmed that the thrust to maintain the orbit was sufficient, even if performed in a cycle of approximately 20 days. At this time, the required thrust was ∆V = 0.006 m/s (fuel consumption of 0.4 g) to maintain the apogee altitude and ∆V = 0.0004 m/s (fuel consumption of 0.024 g) to maintain the perigee altitude. Considering the satellite’s design lifetime of 3 years, approximately 23 grams of fuel would be required. However, it is expected that a larger amount of fuel should be loaded to compensate for orbit changes caused by perturbing forces on the orbit.
6. CONCLUSION
Imagery intelligence plays an important role in identifying key enemy facilities or key targets. Accordingly, satellites capable of capturing high-resolution images in space are essential. To secure high-resolution observation images, large satellites equipped with large optical systems have been used previously. However, it is possible to secure high-resolution images by utilizing small observation satellites and lowering their operating altitude. In this study, we proposed a method for obtaining high-resolution images with a small optical system by using an elliptical orbit and lowering the operating altitude of the satellite. In an elliptical orbit, a design method was proposed that used critical inclination with no argument of perigee change and that applied critical inclination with Sun-synchronous characteristics. The design results indicated that high-resolution optical observation was easy as the perigee was maintained at an altitude of 300 km above the Korean Peninsula, and the local time at which the satellite passed through the ascending node was maintained at 13:00. In addition, the thrust and fuel amount required to maintain the operational orbit of the satellite were predicted, which suggested that long-term satellite operation would be possible at low cost.
The ground revisit period of the orbit designed in this study for the observation area was very large compared to the circular orbit. This means that in the case of a circular orbit, one observation opportunity per day was obtained, whereas for the proposed elliptical orbit, an observation opportunity was obtained once every 4–5 days. Accordingly, for a satellite system using an elliptical orbit, it would be necessary to secure a short revisit period by utilizing a large number of satellites rather than only using one. For a limited area of the Korean Peninsula, a follow-up study on a constellation system that can achieve high-resolution and short revisit period with smaller satellites will be required. Also, for practical analysis, we plan to consider more detailed orbit perturbations, such as solar radiation pressure, the high degree and order of the Geopotential model, and the shape of the satellite.