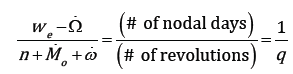1. INTRODUCTION
Satellite constellations were first conceptualized in 1945 by Clarke (1966) who proposed a continuous global coverage constellation consisting of three geostationary Earth orbit (GEO) satellites. The street-of-coverage (SOC) constellation pattern (Luders 1961) as well as Walker star and Walker-Delta constellation patterns (Walker 1971;Ballard 1980) are the most well-known constellation designs for global or zonal coverage. The Flower constellation is a relatively recent discovery that has many potential applications (Mortari et al. 2004). There have also been studies on reducing the number of satellites for continuous global coverage (Beste 1978;Draim 1985;Adams & Rider 1987). A regional coverage constellation has become an option to consider as the types and purposes of space missions become more diversified. The evolution of small or microsatellite technology has resulted in an increasing number of constellation missions for commercial, scientific, or military purposes. The mission objectives are changing from global and general to local and specific. Thus, it can be useful for stakeholders to be able to design and construct a regional coverage constellation that solely focuses on the mission’s specific ground targets (Lee et al. 2019).
Most of the traditional regional coverage satellites were operated on a GEO or geosynchronous orbit so that a specific area could be serviced with a small number of satellites. However, these days, a low Earth orbit (LEO) is the most common choice for microsatellites because of the lower launch cost and the restricted performance of microsatellites. Unfortunately, a LEO not only has a smaller instant coverage range than higher orbits but it is also unable to take advantage of the high eccentricity that provides useful dynamic and geometric features for observing specific local regions. Unlike the Molniya or highly elliptical orbits with a large semi-major axis, it would be risky to choose a high eccentricity orbit for a LEO microsatellite constellation because it would decay faster and have a shorter lifespan. Therefore, in contrast to the traditional design approach, a regional coverage microsatellite constellation needs to be designed for its specific mission objectives while embracing these limitations.
For a regional coverage constellation, Hanson et al. (1990) showed that repeat ground track (RGT) orbits yield shorter revisit times than non-RGT orbits. Ulybyshev (2008) investigated an algorithm to find the best T-P-F (Walker’s notation) Walker-Delta pattern for complex regional coverage using the two-dimensional (2D) geometric coverage map method. He & Han (2007) and Zhang et al. (2018) addressed the regional coverage problem over cities in China using metaheuristic optimization algorithms. Savitri et al. (2017) and Kim et al. (2017) used genetic algorithms to solve the regional coverage problem for the Korean Peninsula. Lee et al. (2019) dealt with a complex regional coverage problem using the common ground track (CGT) constellation pattern with a circular or critically inclined elliptic orbit as a building block. These design approaches can be categorized into three groups. The first is an analytical approach that uses orbital dynamic properties, such as RGT orbits. The second is to use the traditional global or zonal coverage methods such as a Walker or SOC pattern. The third is to solve the optimization problem for the orbital elements such that the figure of merit for regional targets becomes maximum.
In this study, we describe an analytical approach for designing circular LEO microsatellite constellations for discontinuous regional coverage, which is part of the mission design process of a surveillance and reconnaissance mission for the Korean Peninsula. This study contributes to the study of the regional coverage problem in several ways. First, the orbital inclination plays a decisive role in the design of the regional coverage constellation; therefore, we devised an optimal inclination search algorithm that considered both the coverage range of each satellite and the geographical location of the regions of interest. Furthermore, we describe an analytical design process so that users can directly apply it to their own situation without any complex optimization algorithms or iterative dynamic simulations. This is the most distinctive contribution of this study compared with previous studies such as Ulybyshev (2008) and Lee et al. (2019). Thus, this analytical design process can be used in the early stage of the mission design process, allowing fast and simple comparisons between different constellation conditions. Finally, we compare the revisit times of the CGT constellation and the Walker-Delta constellation under optimal and non-optimal inclination conditions. The results of this analysis can be used to determine the appropriate constellation pattern for a given inclination condition (Shin 2021).
The remainder of this paper is organized as follows. Section 2 introduces the optimal inclination search algorithm using the 2D map method and shows the resulting optimal inclinations for single or multiple target problems. This is followed by a description of the design process of the CGT constellation pattern for minimum revisit time. Section 3 describes the hardware and software used to verify the proposed process and algorithms. Section 4 analyzes and compares the revisit times of the constellation proposed in this study and the results from all possible T-P-F Walker- Delta constellations, applying both optimal and non-optimal inclinations. Finally, Section 5 summarizes our conclusions.
2. Optimal inclination for single or multiple target regional co verage
In this section, we describe an algorithm for obtaining the optimal orbital inclination for the given ground targets. Without any dynamic simulation, this algorithm quantifies the observation capability of circular orbits using the geometric relationship between a satellite and ground targets while considering the instant coverage angle of the satellite, such as the payload’s field of view. Here, the 2D coverage map, which was defined by Hanson et al. (1990) as well as Ulybyshev (2008), was used to quantify the observation capability from the area of its graph.
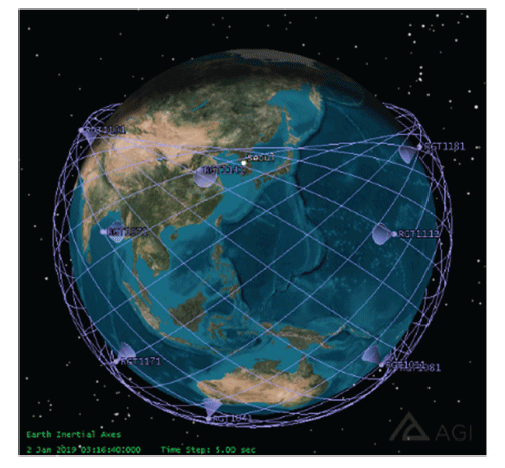
The 2D map takes a 2D space that consists of the argument of the latitude u ε [0˚ 360˚] and the right ascension of the ascending node (RAAN) Ω ε [0˚ 360˚] as its domain. The coverage function f(Ω, u) ≥ 0 maps the Ω-u pairs into a positive real value if it can observe the ground target or 0 if it cannot. To obtain the 2D coverage map, we defined the coverage function f as in Eq. (1). Fig. 1 shows the geometric relationship of the coverage function f. In Fig. 1, θ is the angle from the sub-satellite point (SSP) to the ground target, and ψ is the angle from the SSP to the maximum instant coverage boundary, both measured at the center of the Earth. Using the longitude and geocentric latitude of the SSP (λsat and φsat) and the target (φtgt and λtgt), we can compute the angle θ using cosine rules of spherical trigonometry, as shown in Eq. (2).
Let α be the half angle of the payload’s field of view. Then, the angle ψ is calculated using Eq. (3) (Wertz & Larson 1999). Here, RE is the radius of the Earth and h is the altitude of the orbit.
Then, we can depict the observation capability of the orbit in the 2D graph of the mapping. For example, Fig. 2 shows a graph of the 2D coverage map obtained by computing the coverage function of a circular orbit at an altitude (h) of 500 km and an inclination (i) of 39°. Here, the ground target is Seoul, and the instant coverage angle of the spacecraft is 60°. In other words, theray area in Fig. 2 shows the Ω-u pairs covering the target region (Seoul) by using a circular orbit at an altitude of 500 km and an orbital inclination of 39°.
We have developed an optimal inclination search algorithm to find the optimal inclination such that the orbit obtains the best observation capability. First, we assume that the area of the 2D graph shows the orbit’s observation capability and define it as a value function to be maximized. Note that for circular orbits, the semi-major axis, inclination, location of ground targets, and any type of visible condition, such as the minimum elevation angle or payload’s field of view, must be given. Thus, with a fixed ground target and the payload’s field of view, the optimal inclination (i*) for the circular orbit is defined by Eq. (4). Here, A is the area of the 2D graph, which is a function of a, the semi-major axis, and i is the orbital inclination.
Furthermore, for the multiple target case, the optimal inclination is defined as the inclination that maximizes the weighted sum of the 2D graph area. In Eq. (5), Ak is the k th target’s 2D graph area, wk is its weight, and NT is the total number of targets. In this study, the orbit’s semi-major axis (a) is uniquely determined by the fixed orbital inclination under the RGT orbit condition and restricted altitude range, which will be explained in detail below. Thus, the 2D graph area becomes a function that depends only on the orbital inclination (i).
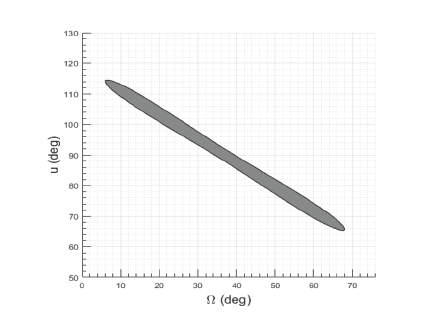
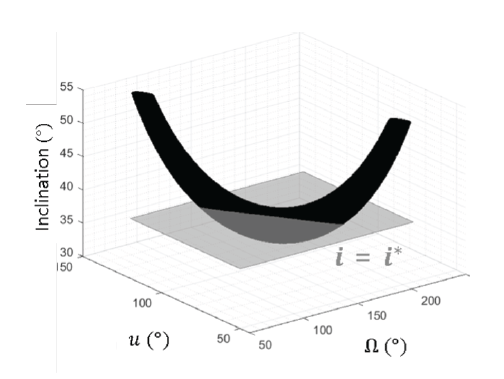
In the algorithm, the 2D graph area or the weighted sum area is calculated within the selectable orbital inclination range with fixed intervals. In this study, for example, we set the inclination range and interval to be 30.0°–89.9° and 0.1°, respectively. Then, the inclination that maximizes the value is selected as the optimal inclination. Fig. 3 is an example expressed in a three-dimensional graph that is a stack of 2D graphs over the selectable orbital inclination range along the z-axis. The figure shows the optimal inclination at which the cross-sectional area is maximized. Fig. 4 shows the pseudocode of the algorithm.
3. Common ground track (CGT) con stellation design
A CGT constellation, which was first named by Lee et al. (2019), is a set of orbits that draws the same ground track and repeats it every certain period. It is essentially one of the Flower constellation patterns that draw closed orbits in the Earth-centered, Earth-fixed coordinate system. If it has symmetry, it can also be classified as a Walker-Delta pattern. However, in this study, we limit the notion of the CGT pattern to constellation patterns that have circular LEO RGT orbits with a repeating period of one nodal day.
Eq. (6) shows the RGT condition with a repetition of one nodal day, where q is limited to 15 for orbits with an altitude of approximately 500 km (Hanson et al. 1990) because of the orbital period. Here, we is the Earth’s rotation rate, n is the mean motion of the orbit, M0 is the reference mean anomaly, and ω is the argument of the perigee of the orbit.
Using the Lagrange planetary equation, Eq. (6) becomes an equation that depends only on the orbital inclination and the semi-major axis. Eqs. (7), (8), and (9) represent the J2–J6 secular effect for each parameter under the circular orbit condition, which is modified from the original equation in Vallado (2013) in that the eccentricity of a circular orbit is considered to be zero. Here, J2–J6 are zonal coefficients of the Earth Gravitational Model 1996 (EGM96). Therefore, given the orbital inclination, we can numerically solve Eq. (6) for the semi-major axis and obtain a-i pairs that satisfy the RGT condition, which leads to the orbit’s semi-major axis being uniquely determined by the inclination under the RGT orbit condition.
To design a CGT constellation, it is necessary for the constellation to satisfy the conditions to draw the same ground trajectory. Given the number of satellites (N) and the number of revolutions of the RGT orbit in its repeating period (q), the orbital plane arrangement condition (ΔΩ) and the spacecraft’s orbit phase difference condition (Δu) are determined. Eqs. (10) and (11) show the multiplane CGT condition with the minimum revisit time. This is rewritten from the general equation in Ortore et al. (2017) to become the equation for circular RGT orbits with a repeating period of one nodal day. Here, N is the total number of spacecraft, and ΔΩj,j–1 and Δuj,j–1 are the differences between the (j – 1)th and j th spacecraft’s RAAN (Ω) and argument of latitude (u), respective, where j = 1, …, N – 1. Although an asymmetric CGT constellation is available using this equation, we set ΔΩ to a constant value of 2π / N to evenly distribute the orbit planes, which makes the constellation a symmetric CGT constellation.
To complete the constellation design, we set the reference orbit for the CGT constellation that passes over the target at a given moment t0. For the target whose geocentric latitude is smaller than the orbital inclination, the reference spacecraft’s RAAN (Ω0) is calculated using Eq. (12) by referring to Fu et al. (2012). In addition, the argument of latitude (u0) is calculated using the sine rule of spherical trigonometry, as shown in Eq. (13). S is the Greenwich mean sidereal time.
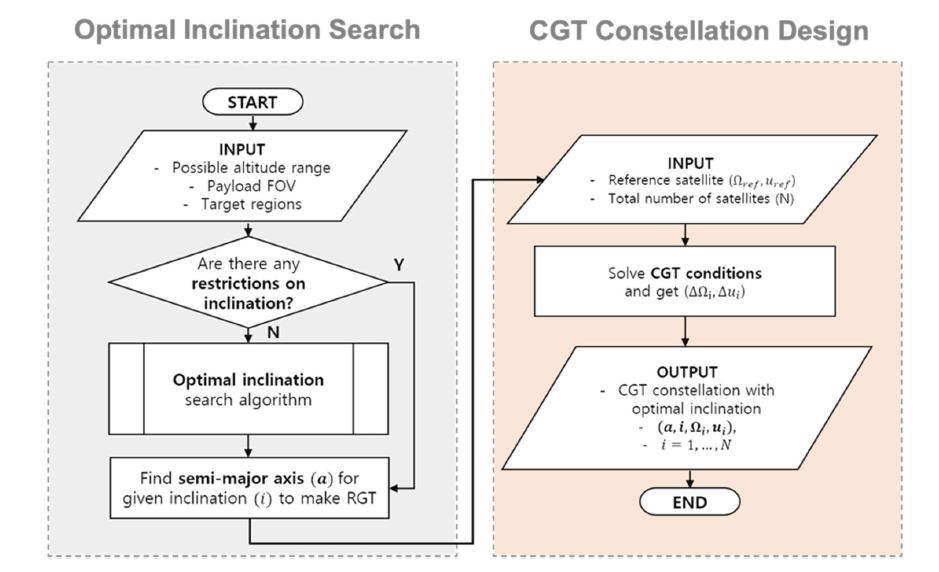
To summarize, a circular orbit constellation with constant altitude and inclination needs 2N + 2 parameters. In this study, we present a step-by-step design process to obtain the parameters for the CGT constellation with the optimal inclination. First, two parameters, the semi-major axis, and the inclination, are determined by the one nodal day RGT condition and the optimal inclination condition. Next, the reference spacecraft’s RAAN (Ω0) and argument of latitude (u0) are determined, forming the reference orbit for the constellation. Finally, the CGT constellation condition determines the rest of the 2N-2 parameters, ΔΩj,j–1 and Δuj,j–1 (j = 1, …, N-1), which is summarized in Figs. 5 and 6 shows the overall design process of the CGT constellation with optimal inclination. The architecture of the design process is divided into two parts: the optimal inclination search process and the CGT constellation design process. If there is no orbital inclination constraint for the design problem, the optimal inclination search algorithm finds the best orbital inclination that maximizes the observational capability considering the given ground targets. Then, it calculates the semi-major axis that satisfies the RGT orbit conditions. Note that the repeating period of the RGT is set to be one nodal day for the minimum revisit time. Finally, the remaining orbital parameters are calculated by solving the CGT conditions using the reference orbit that passes over the target at a given moment.

4. Results and Discussion
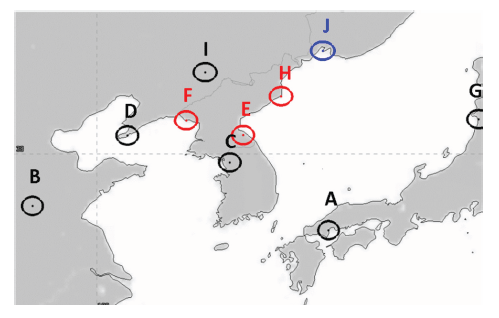
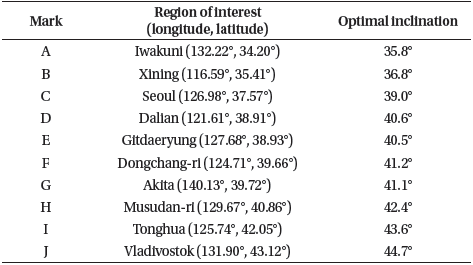
Fig. 7 shows 10 regions of interest near the Korean Peninsula, which are the ground targets for the constellation design with optimal inclination. Each target’s boundary was set to have a radius of 50 km. The mission satellite had a limited instant coverage range with a payload field of view of 60° and orbit altitude of approximately 450–550 km. Thus, we can call this type of design problem a discontinuous regional coverage problem with low earth orbit (LEO) conditions.
With a fixed field of view of 60°, the half angle of the instant coverage range (α) is 30°, and the corresponding ψ is between 2.4° and 2.9° if the altitude ranges from 450 to 550 km. Under these conditions, the 2D map is calculated for the entire domain by dividing Ω and u every 0.25° from 0° to 360°. After the calculation, the algorithm separately saves the area of the graph for each ground target. Finally, the algorithm repeats the process to determine the optimal inclination that satisfies Eq. (1) by dividing the orbital inclination i every 0.1° within the inclination search space. Considering the latitude of the ground targets in Table 1, the inclination search space is between 30° and 90° because the orbit with an inclination under 30° does not have any observation coverage of the targets. Table 1 shows the optimal inclination results for the 10 regions of interest in Fig. 7. As a result, the values of the optimal inclination tended to be slightly greater than those of the target’s geodetic latitude, and the average of the inclination-latitude difference was approximately 1.5°.
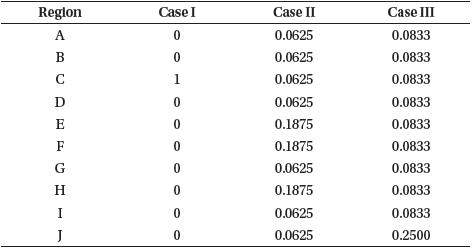
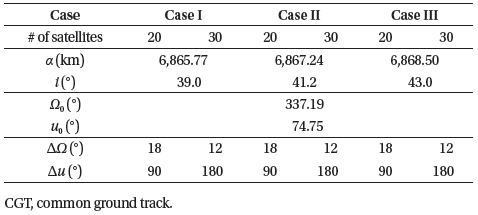
To construct the regional coverage problem, we defined three different constellation design cases. The first design case (Case I) takes region C as the only ground target, and the second and third cases (Case II and Case III) included all 10 regions of interest shown in Fig. 7, but with different sets of weights. The optimal inclination search algorithm uses the weights in Table 2 while computing the weighted sum of the 2D-map area in Eq. (2). For the multi-target cases (Cases II and III), the weights are scaled such that the values of the main targets (E, F, and H for Case II, and J for Case III) are three times higher than the others, but the total sum of the weights = 1. As a result, the algorithm returned inclinations of 39.0°, 41.2°, and 43.0° for Cases I, II, and III, respectively. By combining the optimal inclination and the CGT constellation pattern, we constructed optimally inclined CGT constellations using 20 and 30 satellites for each case. Table 3 shows the overall constellation configuration, where the epoch of the orbital elements is January 1, 2019, 12:00:00.000, UTC as an example. Fig. 8 shows the Case I CGT constellation design with 20 satellites.
To measure the revisit times over each region, we set the maximum, average, and minimum revisit times as the figures of merit. Here, the revisit time is defined as the duration of the coverage gap between successive observations of the area of interest. During the simulation, the revisit time was recorded for every coverage gap, and the maximum and minimum values were the maximum and minimum revisit times, respectively. The average revisit time was defined as the sum of all durations divided by the total number of gaps. In this study, the revisit time was obtained by a 2-month numerical simulation using a high-precision orbit propagator from AGI’s Systems Tool Kit. The integrator was a Runge-Kutta 7–8th order. The force models for the perturbation environment were 21 × 21 EGM96 models for the central body gravity. The Jacchia–Roberts atmospheric density model was also used with a drag coefficient of 2.2, area-to-mass ratio of 0.0029, third-body gravity of the Sun and Moon, solar radiation pressure with a solar flux index (F10.7) of 150, and spacecraft reflectivity of 1.0.
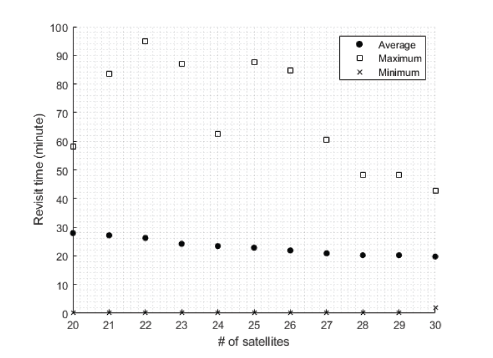
First, as a result of the simulation of the single ground target case (Case I), the maximum, average, and minimum revisit times of the optimally inclined 20-satellite CGT constellation were 58.1 min, 27.9 min, and 0.2 min, respectively. This means the designed constellation pattern ensured a revisit time of less than 60 min with 20 satellites, without any orbital maintenance such as stationkeeping control, for two months. For the 30-satellite CGT constellation, the values were 42.5 min, 19.7 min, and 2.0 min, respectively.
We performed additional simulations for Case I with various constellation sizes while gradually increasing the number of satellites from 20 to 30 (Fig. 9). The result shows that the average revisit time decreases almost linearly with the slope of −0.98 min/satellite as the constellation size increases. The maximum revisit time, however, does not seem to have a strict linear relationship with the size of the constellation, which indicates that the revisit efficiency of the symmetric CGT constellation varies with the number of satellites. In other words, the observation pattern and efficiency change as the size of the CGT constellation varies. Indeed, for the maximum revisit time, not only are the differences between the 20-, 24-, and 27-satellite CGT constellations < 5 min despite their different sizes, but also the CGT constellations with 21–27 satellites have maximum revisit times that are longer than the 20-satellite CGT constellation.
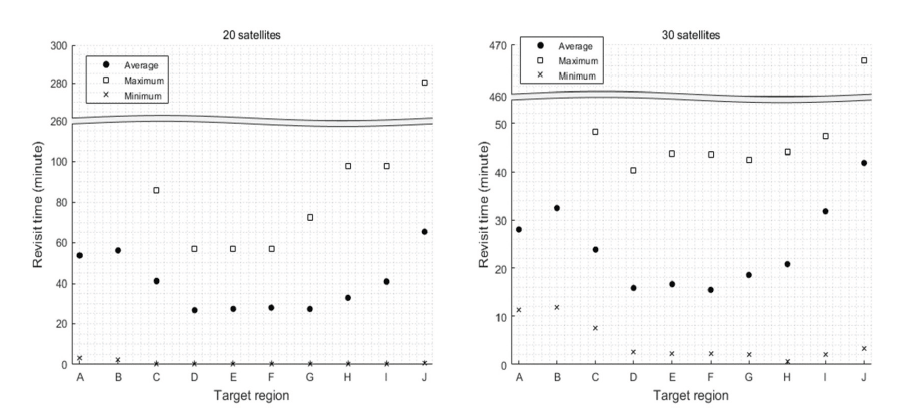
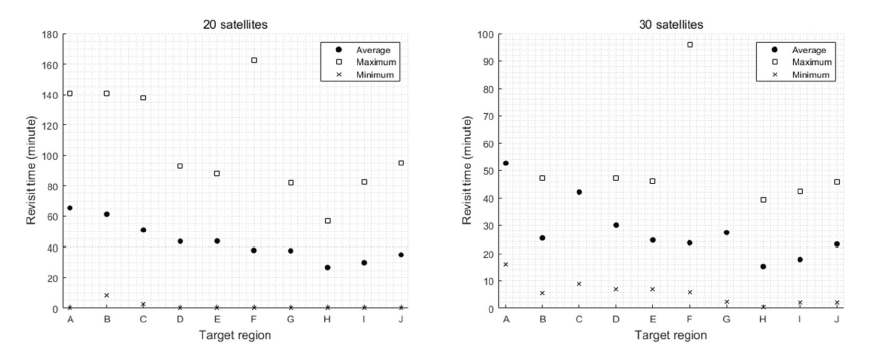
The results of Cases II and III, the multiple target cases, are shown in Figs. 10 and 11, where the target regions are arranged along the x-axis by latitude in ascending order. The average revisit times of individual regions with 20 satellites were all less than 70 min, and those of weighted regions were less than 40 min in both cases. Because the optimal inclination of an individual ground target is highly dependent on its latitude, it is clear that the region whose optimal inclination is close to the resulting inclination (41.2° in Case II and 43.0° in Case III) have shorter revisit times than others. For example, in Case II, the average revisit times of regions D and G are close to those of regions E, F, and H, the weighted regions, within 5 min, although they are not highly weighted. In Case III, the average revisit time of region J is almost half of the time in Case II, whereas those of regions A–G are longer than those in Case II. Similar to Case II, regions located in the latitude far from that of region J tend to have longer revisit times compared to regions that are closer to region J.
To compare the CGT constellation to all possible T – P – F combinations of the Walker-Delta pattern, we first simulated the full set of Walker-Delta patterns given 20 or 30 satellites, and for every available number of planes (P), we selected the best F with which the resulting Walker- Delta constellation had the shortest average revisit time. We then compared the results from the CGT constellation with those from the best Walker-Delta patterns for both optimal and non-optimal inclinations. Note that the symmetric CGT constellation is a part of the Walker-Delta constellation with P = T orbital planes given T satellites and the phasing parameter F satisfying the CGT condition. Thus, 20- and 30-satellite CGT constellations can be represented by 20-20- 5 and 30-30-15 Walker-Delta constellations by calculating using Eqs. (10) and (11). Finally, the numerical simulations were performed for two months within the J2-perturbation environment, and the inclination-altitude pairs for the RGT condition were computed only for the J2 secular effect.
First, Fig. 12 shows the results of 20-satellite and 30-satellite constellation patterns with the optimal inclination for Seoul (39.0°). For the 20-satellite constellations, the CGT pattern had the shortest maximum revisit time. Furthermore, the maximum revisit time decreased with an increasing number of orbital planes. For the 30-satellite constellations, however, a 30-6-5 Walker-Delta pattern had the shortest maximum revisit time (23.5 min). In contrast, the maximum revisit time of the 30-satellite CGT constellation was 40.5 minutes. Meanwhile, the average revisit time was almost the same to within approximately 3 min for both the 20- and 30-satellite constellations.
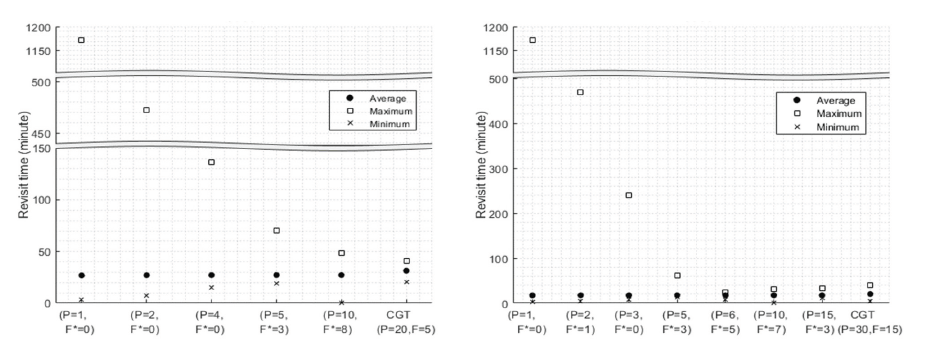
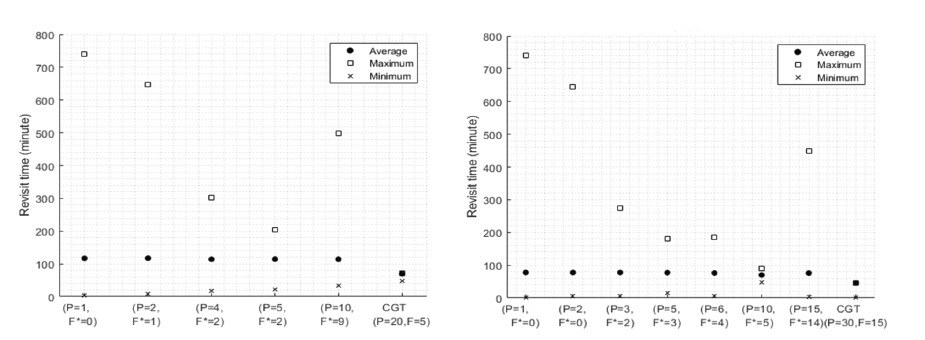
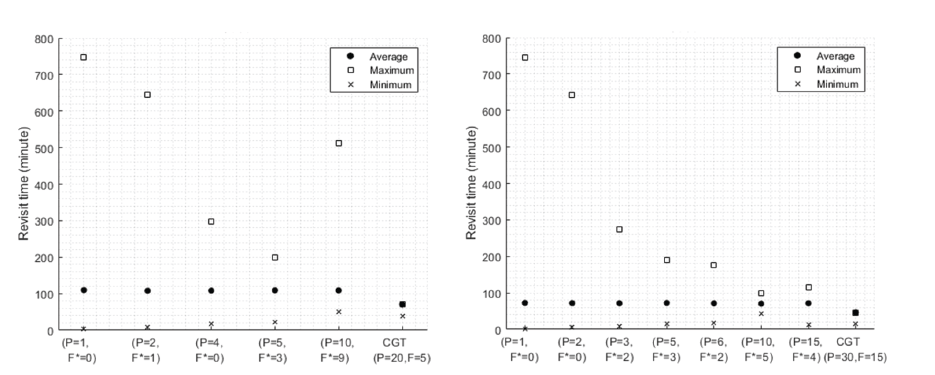
Next, two types of inclinations were considered as the non-optimal inclination cases. One was the inclination of 82.0° (Fig. 13) relating to the launch angle restriction for a direct launch from the Korean Peninsula. The other was the inclination of 97.6°, which satisfied both Sun-synchronous and RGT conditions under J2 perturbation, at an altitude of 561 km (Fig. 14). For these cases, the CGT constellations had the shortest maximum and average revisit times. These times happen to be the same with a maximum and average revisit time of approximately 70 min for 20 satellites and 46 min for 30 satellites. These times are close to 24 h divided by the number of satellites. This is because the RGT condition had been set to repeat its ground track every one nodal day, which leads to at least one access to the target each day. Finally, for both non-optimal inclination cases of i = 82.0° and i = 97.6°, the best Walker-Delta patterns with P < T were the 5-plane constellations for 20 satellites, and the 10-plane constellations for 30 satellites.
5. Conclusion
In this study, we describe an analytical method to design constellations in circular LEOs for discontinuous regional coverage. The search algorithm proposed can determine the best inclination for a given constellation that maximizes the coverage for single or multiple ground regions. The optimal inclination search algorithm considers both the coverage range of the satellite and the location of the regions of interest. As a result, this study suggests optimal inclinations for single or multiple ground regions. For Seoul, for example, 39.0° was obtained as an optimal orbital inclination, and the maximum and average revisit times were 58.1 min and 27.9 min for a 20-satellite constellation, and 42.5 min and 19.7 min for a 30-satellite CGT constellation, respectively. Using the proposed algorithm, the revisit times of the CGT constellation were verified by comparing them with those of the Walker-Delta constellation under optimal and nonoptimal inclination conditions. It is clear that the CGT constellation had the shortest revisit times with a nonoptimal inclination condition. The results of this analysis can be used to determine the appropriate constellation pattern for any specific inclination condition. The analytical and step-by-step design process yields efficient and optimal results so that there is no need to wait for a lengthy convergence or dynamic simulations, which leads to a faster overall design process for any specific number of satellites. Therefore, it can be used in the early stage of the mission design phase, allowing fast and simple comparisons between different constellation conditions.