1. INTRODUCTION
Korea’s first lunar mission, the Korea Pathfinder Lunar Orbiter (KPLO), is being progressed by the Korea Aerospace Research Institute (KARI) (Ju et al. 2013). The KPLO program has been recently modified based on development issues and the KPLO will be launched in the middle of 2022. The Earth-Moon Transfer phase of the KPLO consists of a 3.5 phasing loop, which includes two perigee (PM) and Lunar orbit insertion (LOI) maneuvers. Additional details on the KPLO mission and trajectory are reported in the literature (Ju et al. 2013;Choi et al. 2018;Song et al. 2018;Kim et al. 2019).
The flight dynamics system (FDS) of the ground system is essential in ensuring a stable and successful mission planning and operation. The most important elements for space navigation are orbit determination (OD) and state prediction capability. To ensure successful flight dynamics operations, KARI designed a dual-simulation engine, consisting of a commercial off-the-shelf (COTS) simulation engine and a KARI simulation engine (Song et al. 2018). Numerous studies (Song et al. 2014;Song et al. 2016;Bae et al. 2017;Song et al. 2017) have discussed development strategies, requirements, burn performances, and contingency designs for the development and implementation of the KPLO FDS. For the OD, the COTS simulation engine employs a sequential estimation based on an extended Kalman filter (EKF) and a backward smoother. The KARI simulation engine utilizes a batch estimation method that is based on a least-square filter. This engine uses in-house codes from previous flight dynamics heritage and developed prototypes (Lee et al. 2017, Kim et al. 2017). In order to guarantee a stable performance, the COTS simulation engine will be used as a primary tool for the flight dynamics operations of the KPLO. The KARI simulation engine can be used as a main tool for the space exploration after actual performance validation of the KPLO mission.
The navigation performance can vary depending on the OD and flight dynamics operation strategies. The performance of the OD is a critical factor for mission planning, operation, and payload data processing. The length of tracking arcs is an important aspect to consider in order to control the accuracy level of the OD; moreover, the arc length directly affects the OD accuracy and consistency. The analysis of the KPLO mission orbit periods was presented in a previous paper, in which the authors recommended a 48-hr tracking OD strategy (Kim et al. 2018). The choice of a long tracking arc can ensure accurate estimation results for the OD; however, limited data processing resources and validation time, an irregular maneuvers schedule, and operational constraints restrict the OD arc length to several days. The main issue related to the Earth-Moon Transfer phase is navigation performance, which is critical for accomplishing successful maneuvers. The chosen 3.5 phasing loop trajectory includes several PM and LOI burns; therefore, the performance of the OD during the maneuver time is particularly critical. As a result, to ensure the best possible navigation performance, it is necessary to investigate the arc-length effect on the OD during the Earth-Moon Transfer phase.
In previous lunar exploration missions, various OD arc lengths have been tested to achieve the target navigation performances. Kim et al. (2018) summarized the strategies used to select the OD arc lengths for various missions. Because each mission has its own requirements, mission constraints, maneuver plans, mission trajectory, and orbits, it is impossible determine “the best” arc length selection strategy for lunar missions. In order to the optimal OD arc length for a specific mission, it is important to analyze and determine an OD plan through a pre-launch OD analysis. For what concerns the Earth-Moon Transfer phase of most lunar missions, the OD performance is expected to be lower than that of the lunar mission phase; in fact, payload data processing and mission planning (e.g., measuring, imaging, and monitoring) are not commonly included in the objective of trans-lunar navigation. Therefore, it is indispensable to investigate the effect of the OD arc-length selection and determine the optimal arc length for the KPLO OD during the Earth-Moon Transfer phase.
In this study, focused on the KPLO trans-lunar orbits, the OD results were examined using a sequential estimation technique; moreover, the OD performance was estimated according to the length of the tracking arc for daily-OD. During the trans-lunar phase of real mission operations, various maneuver events (e.g., PM, LOI, momentum unloading, and test burns) affect the behavior of the OD; however, in order to examine in detail the arc-length effect, maneuvers and contingency events were ignored in this study.
Section 2 describes the true orbit and the measurement simulation step. The OD setting and strategy (e.g., dynamics and measurement modeling setting, estimation technique, and quality assessment philosophy) are summarized in Section 3. In the same section, various OD arc-length cases are introduced. Section 4 presents the results of the arclength effect investigation for the KPLO OD during the Earth-Moon Transfer phase (consisting of three parts: launch–PM1, PM1–PM3, and PM3–LOI). Finally, Section 5 summarizes the conclusions of this study.
2. MEASUREMENT SIMULATION
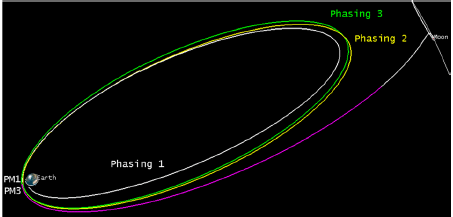
A simulated true orbit, presented in a previous paper (Kim et al. 2019), was used for the measurement generation of the KPLO in the trans-lunar phase. Fig. 1 shows the true orbit of the KPLO Earth-Moon Transfer phase in an Earth-centered inertial frame. The hypothetical Earth-Moon Transfer phase was set to include two maneuvers: PM1 and PM3. The translunar phase was programmed launch for December 26, 2020 at 07:22:17 (UTC), PM1 for January 3, 2021 at 05:25:10 (UTC) (by an impulsive burn), PM3 for January 19, 2021 at 17:10:15 (UTC), and the first LOI maneuver (LOI-1) for January 24, 2021 at 16:56:52 (UTC). Additional information about the maneuvers is shown in Table 1. Choi et al. (2018) and Kim et al. (2019) described a particularly detailed KPLO trans-lunar trajectory using a 3.5 phasing loop. The dynamic modeling information for the KPLO Earth-Moon Transfer true trajectory is summarized in Table 2. In order to account for the Earth gravity effect, the EGM2008 model was applied with a degree of 21 and an order of 21 (Pavlis et al. 2012). JPL DE430 was utilized for the determination of planetary ephemeris and perturbations caused by both solar radiation pressure and third bodies (Sun and Moon). The general relativity effect was not considered in the generation of the true trajectory. The Runge-Kutta 7–8 integration method (with a variable step) was employed for numerical integration.

|
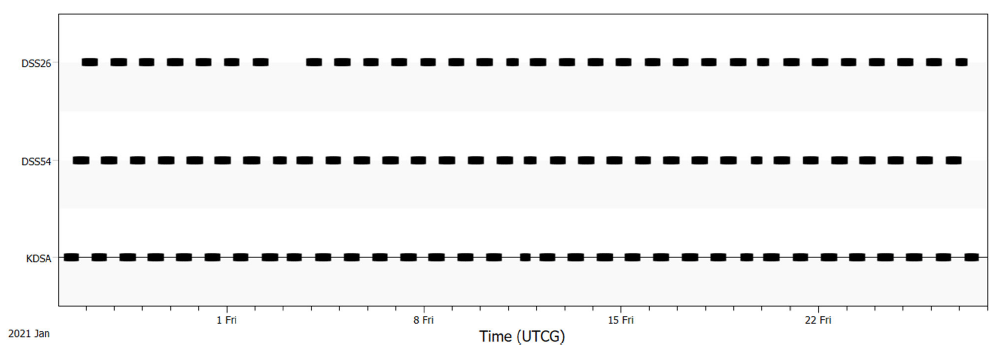
The KPLO measurements were generated considering a three-ground-station configuration and simulating the true trajectory. The pseudo-noise (PN) range and the Doppler tracking data by two deep space network (DSN) antennas and the Korea Deep Space Antenna (KDSA) were simulated at 60-s intervals. The antennas located at Goldstone, Madrid (DSN), and Yeoju (KDSA) were regarded as communication and tracking stations. The continuous tracking duration was restricted to 2 hrs, followed by a 1-hr break. Multiple tracking by the two ground stations was not allowed. The simulated KPLO measurements for the trans-lunar phase are shown in Fig. 2.
The measurement error statistics were accounted for by using the specifications of the KDSA hardware and the values of the DNS service catalog for the tracking data simulation (JPL 2015). Additionally, we used the performance analysis results for the KPLO communication and tracking obtained through sequential and PN ranging techniques (Park & Moon 2018). In order to considering the transponder delay variation uncertainty and the tracking accuracy, the ranging noises of the DSN and KDSA were set to 13 m and 22 m, respectively. The sigma values of the Doppler measurement noises of the DSN and KDSA were set instead to 0.003 Hz and 0.15 Hz, respectively. The Doppler noise values, originally expressed as velocities (mm/s), were converted into cycles (Hz) to allow software implementation (Woodburn et al. 2015). Space environmental effects (e.g., tropospheric refraction and ionospheric delay), which can bias or distort the range and Doppler results, were considered in the measurement simulation. In particular, in order to determine measurement and time biases, we applied the Gauss-Markov and random walk models, respectively. Both of these models were chosen for their simplicity. The Gauss-Markov model is based on a scalar exponential Gauss-Markov sequence, which is the natural model for the measurement of bias modeling; meanwhile, the random walk model is able to determine the simple evolution characteristics of time biases.
3. ORBIT DETERMINATION
In this section, we demonstrate the strategy adopted for the study of the KPLO OD (sequential estimation for the Earth-Moon Transfer phase) and the configuration of the OD arc-length effect investigation. For the KPLO OD, we utilized a sequential filter based on the EKF and a backward smoother of the ODTK software (Vallado et al. 2010). The mission operation and analysis capability have been determined through sequential estimation techniques derived from the IBEX, LRO, and LADEE missions (Policastri et al. 2009;Slojkowski et al. 2015;Policastri et al. 2015a, b). The COTS simulation engine of the KPLO FDS employs the same sequential estimation methods of the ODTK; therefore, our analysis results can be used to examine the actual performance of the KPLO flight dynamics operation.
The dynamic modeling settings for the KPLO OD in the Earth-Moon Transfer phase are shown in Table 2. The same modeling configuration to establish the true trajectory was applied in the investigation of the arc-length effect. Media corrections (e.g., tropospheric reflection and ionosphere delay) were considered during measurement modeling, parallelly with the plate motion of the ground station and the antenna correction. The measurement and time bias estimations were accomplished during the OD process. The Runge-Kutta 7–8 integration method (with a variable step) was utilized for the numerical integration of the state propagation.
The OD for the KPLO was achieved considering a daily schedule and using a fixed tracking arc length [we used the same OD configuration applied to the trans-lunar phase in Kim et al. (2019)]. The fixed arc length-based daily OD was accomplished; afterward, in order to evaluate the orbit quality, we calculated the overlap period between the two arcs. The estimation parameters included: the state of the spacecraft (i.e., position and velocity), the solar radiation pressure coefficients (Cr), and the transponder’s and station’s biases. The initial orbit position uncertainties for the radial, along-track, and cross-track directions were assumed to be 300 m, 1,000 m, and 200 m, respectively [as in Kim et al. (2019)]. The OD calibrations by fine filter tuning were not included in our OD analysis. For the trans-lunar phase, the length of the OD arc can be shortened due to maneuver schedule and the operation; however, based on our arclength effect examination, we assumed a fixed arc length for OD. Six cases, corresponding to periods of 24 hrs, 48 hrs, 60 hrs, 3 days, 4 days, and 5 days, were considered for the OD arc-length investigation. Hence, we analyzed the OD results obtained for these different arc lengths during the launch– LOI phase. The orbit maneuvers (i.e., PM1 and PM3) were excluded in this study. Therefore, three main phases were finally considered: launch–PM1, PM1–PM3, and PM3–LOI.
In order to evaluate the quality of the KPLO OD orbit, we investigated the orbit uncertainty (by error covariance), the orbit overlap precision, and the external orbit comparison by considering the differences between the true and estimated trajectories. All the results (i.e., uncertainties and differences) were calculated in the radial, along-track, and cross-track directions, and their total 3D position values were used to determine the arc-length effect. Moreover, the mean and standard deviation values of the different phases were used to determine the OD performance, in accord with the arc-length selection strategy. Notably, the orbit uncertainties were calculated using 3 sigma values.
4. RESULTS
In this section, we describe the three phases (i.e., launch–PM1, PM1–PM3, and PM3–LOI) through which we performed the OD, as well as their accuracies with respect to the arc length. The investigation of the arc-length effect on the OD was conducted considering tracking arcs of 5 days, 4 days, 3 days, 60 hrs, 48 hrs, and 24 hrs, for a total of 29 days.
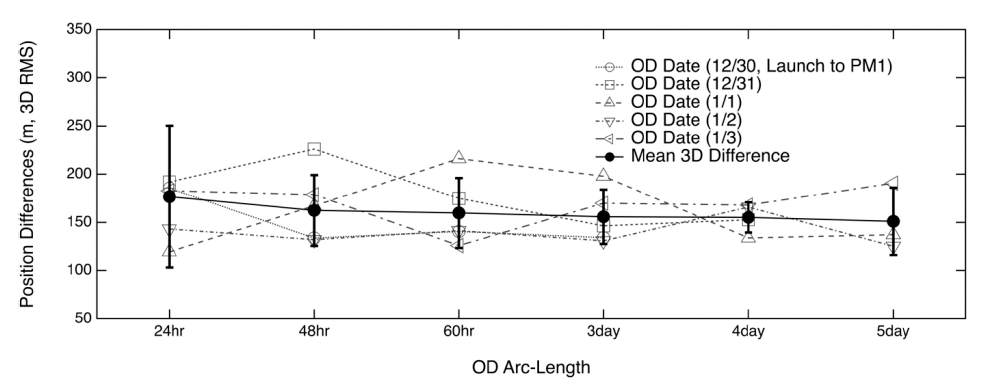
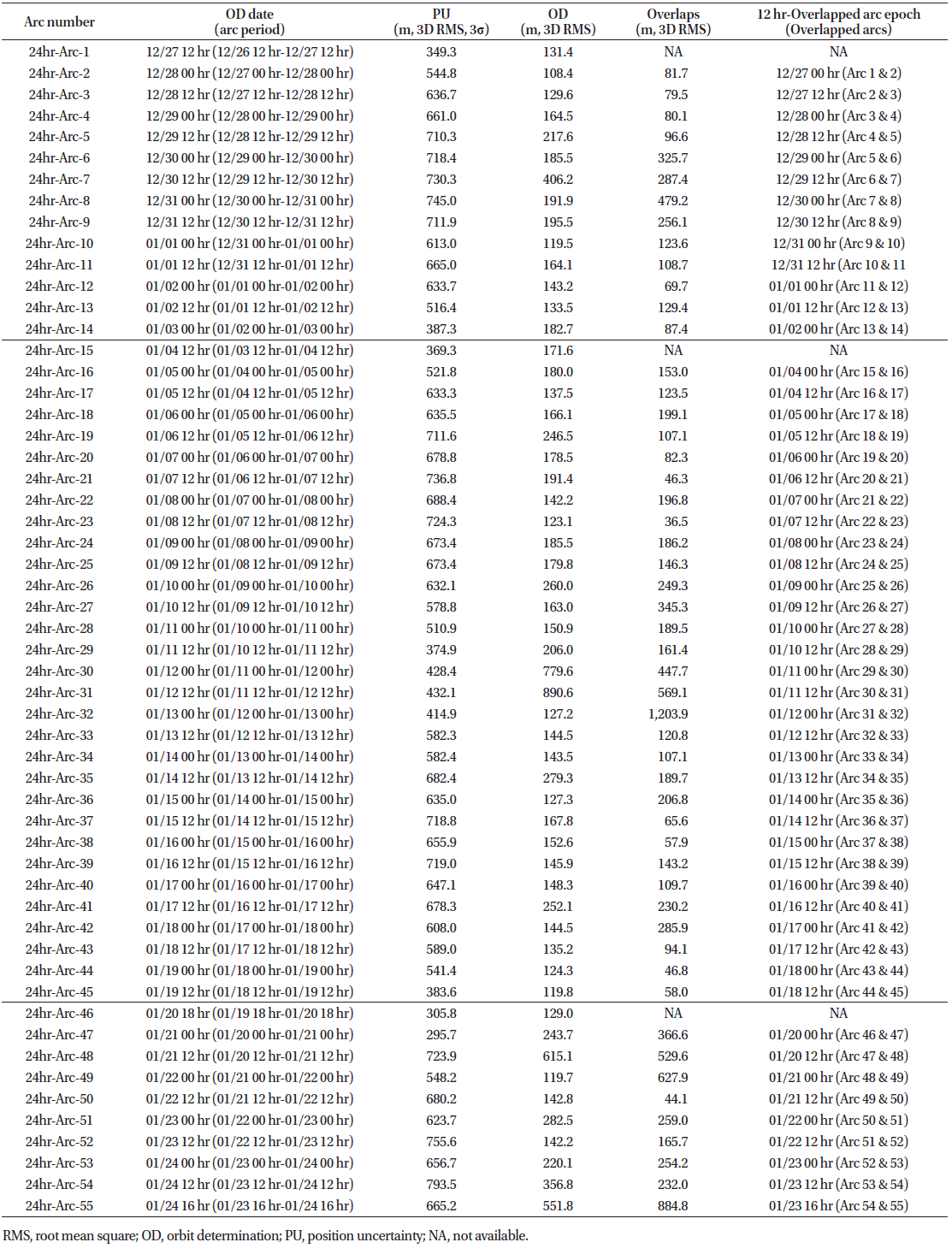
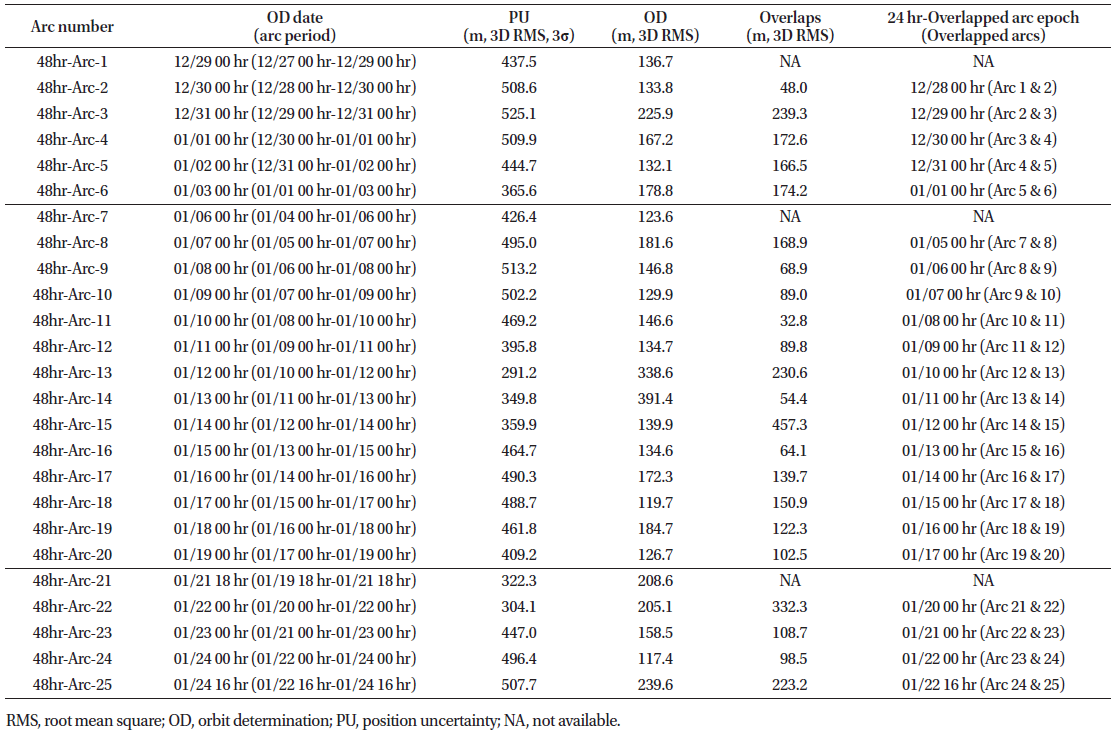
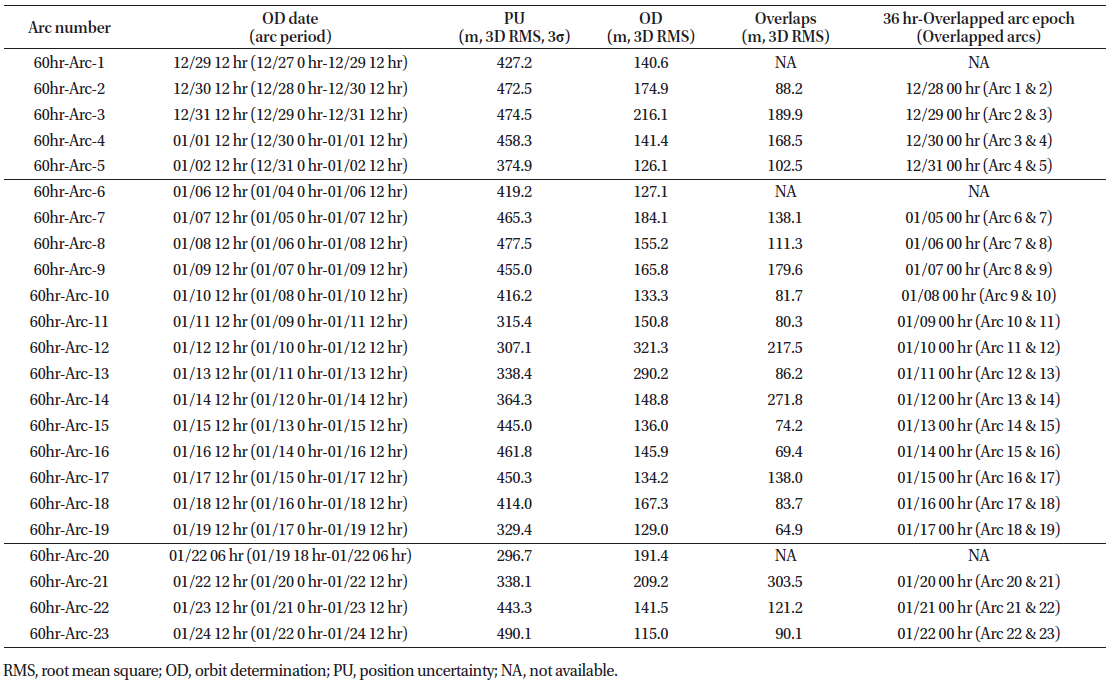
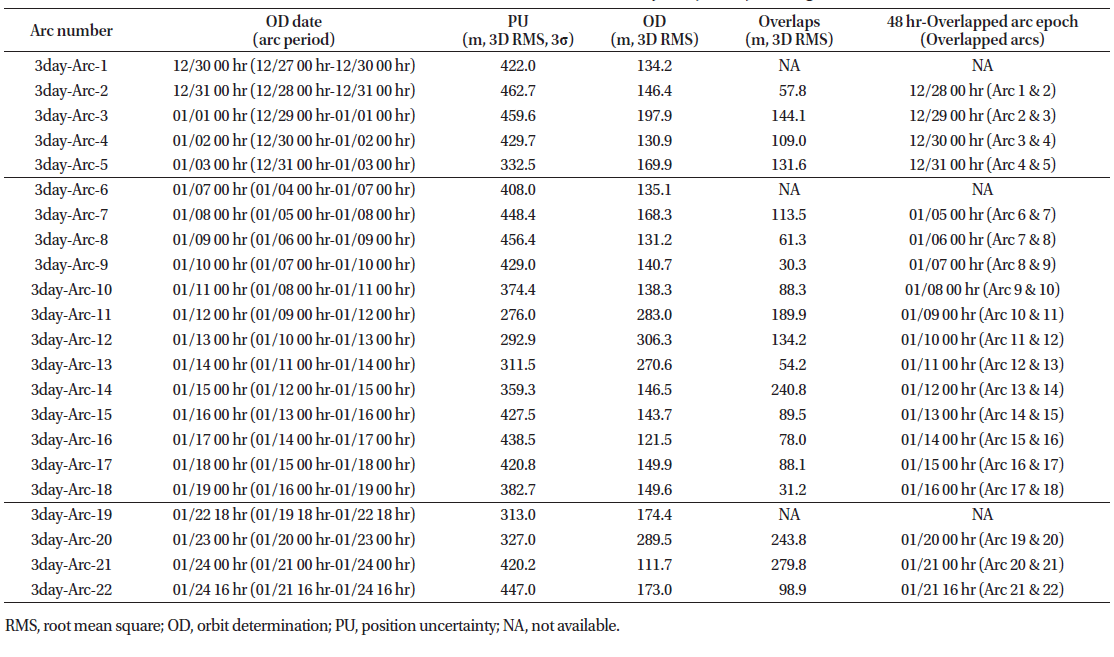
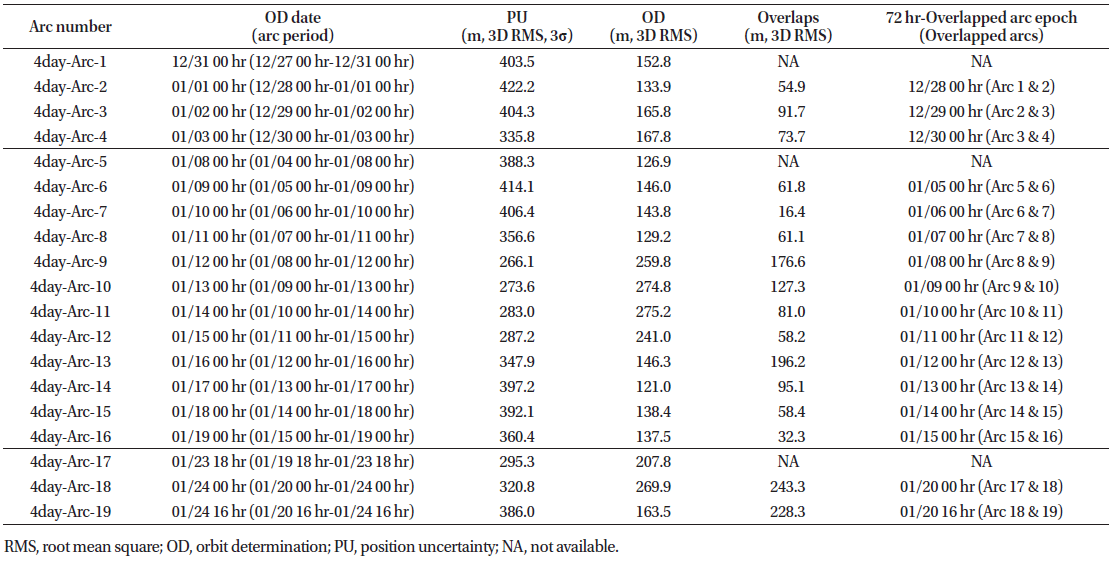
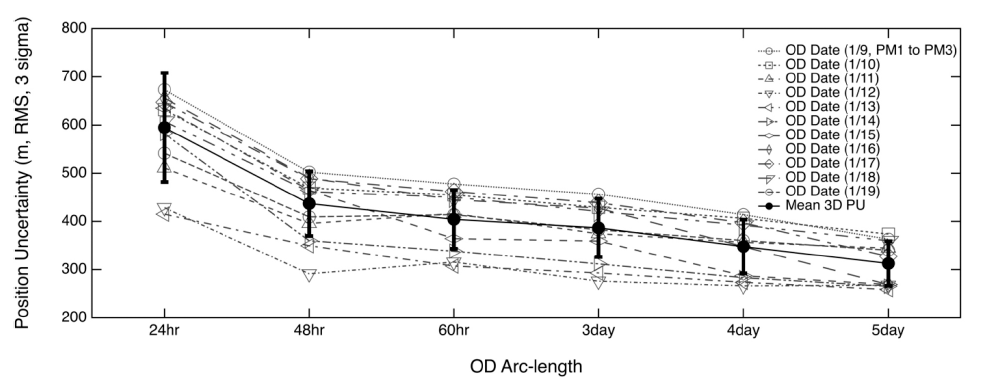
The OD results relative to the launch–PM1 phase are presented in Figs. 3–5: the thick solid lines indicate the mean values of the position uncertainties for all cases, accompanied by the standard deviation error bars; the other lines indicate some results selected among all the OD dates. The OD results for all cases are shown in Tables 3–8. We obtained 14 OD results based on the 24-hr tracking arc for the launch–PM1 phase (Table 2), but only three results based on the 5-day tracking arc OD (Table 8). Since the results obtained for all cases could not be described in one figure, we created several figures; in each of them, we presented only the data corresponding to all the arclength cases having a specific period. A daily schedule was employed for the OD cases with 5-day, 4-day, 3-day, 60-hr, and 48-hr arcs, while a 12-hr schedule was employed for the 24-hr arc OD (for the organization of the orbit overlap period). Table 4, 5, 6, 7
|
|
|
|
|
|
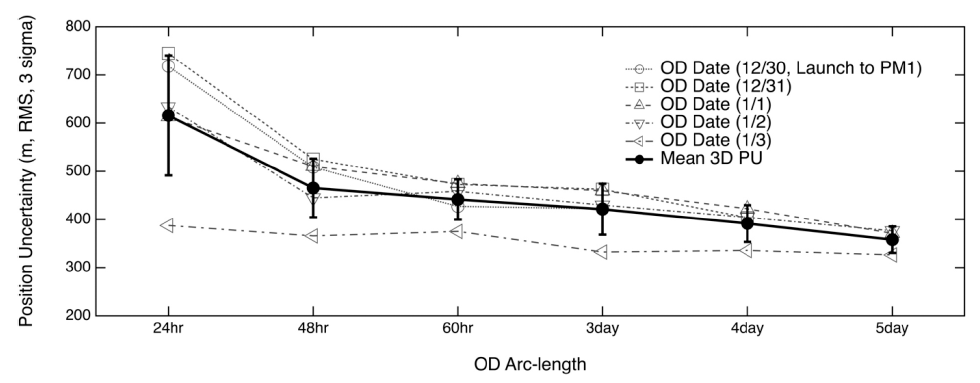
Fig. 3 shows the 3D total position uncertainties of six arclength OD settings: the data show that longer arc lengths corresponded to more precise and stable OD results. The mean position uncertainty values were 615.9 m, 465.3 m, 441.5 m, 421.3 m, 391.5 m, and 357.9 m for the 24-hr, 48-hr, 60-hr, 3-day, 4-day, and 5-day arc-length cases, respectively (Table 9) ; meanwhile, the standard deviation values corresponded to 124.6 m, 61.0 m, 41.8 m, 52.8 m, 38.1 m, and 27.3 m, respectively. For the 24-hr arc OD, the mean and standard deviation values were larger, reflecting a large dispersion.
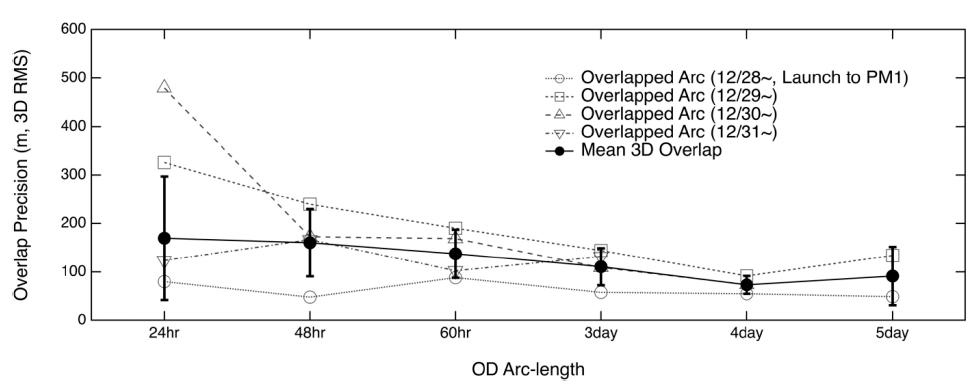
Fig. 4 and Tables 3–8 show the orbit overlap differences before PM1. The orbit overlap differences were of 169.6 m, 160.1 m, 137.3 m, 110.6 m, 73.4 m, and 91.5 m for the 24-hr, 48-hr, 60-hr, 3-day, 4-day, and 5-day arc lengths, respectively; meanwhile, the standard deviation values corresponded to 127.5 m, 69.3 m, 49.5 m, 38.1 m, 18.4 m, and 60.0 m, respectively.
Fig. 5 shows the OD accuracy (i.e., the difference between the true and estimated orbits) before PM1. The orbit differences corresponded to 176.7 m, 162.4 m, 159.8 m, 155.9 m, 155.1 m, and 151.1 m in the case of the 24-hr, 48-hr, 60-hr, 3-day, 4-day, and 5-day arc lengths, respectively; meanwhile, the standard deviation values corresponded to 73.7 m, 36.7 m, 36.2 m, 28.0 m, 15.6 m, and 34.8 m, respectively. Figs. 3–5 and Table 9 show how OD precision and accuracy improved with increasing arc length; moreover, the OD performance did not improve drastically by increasing the arc length over 3 days.
Table 9 demonstrates that the precision and accuracy of the OD before PM1 were of 420 m (based on the 3 sigma values), 110 m, and 156 m (based on a > 3-days OD strategy).
A lot of OD arcs were investigated for the PM1–PM3 phase. The OD results are shown in Figs. 6–8; moreover, the results of all arcs for the PM1–PM3 phase are contained in Tables 3–8. Fig. 6 shows the OD position uncertainties for various arc lengths in the PM1–PM3 phase. The mean values of the six arc-length cases were 594.9 m, 437.0 m, 404.2 m, 386.6 m, 347.7 m, and 312.6 m for the 24-hr, 48-hr, 60-hr, 3-day, 4-day, and 5-day arc-lengths, respectively; moreover, the correspondent standard deviation values were 113.0 m, 67.2 m, 60.8 m, 60.6 m, 55.7 m, and 46.5 m, respectively. Notably, the position precision was improved by increasing the tracking arc length from 24 hrs to 5 days; the standard deviation trend showed similar features. Fig. 7
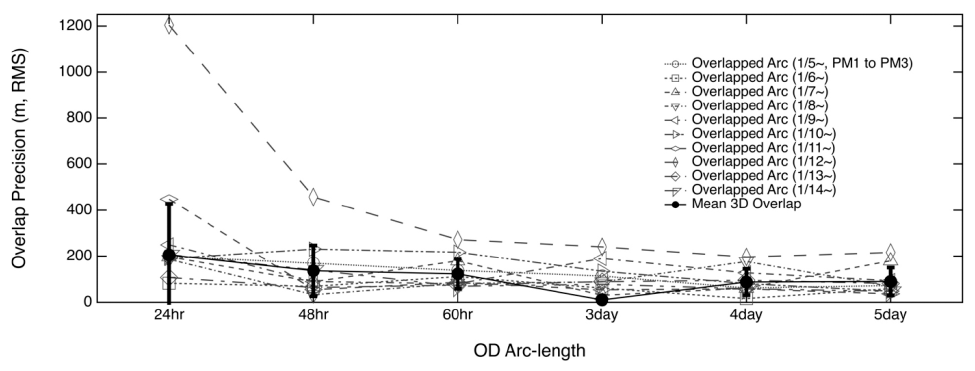
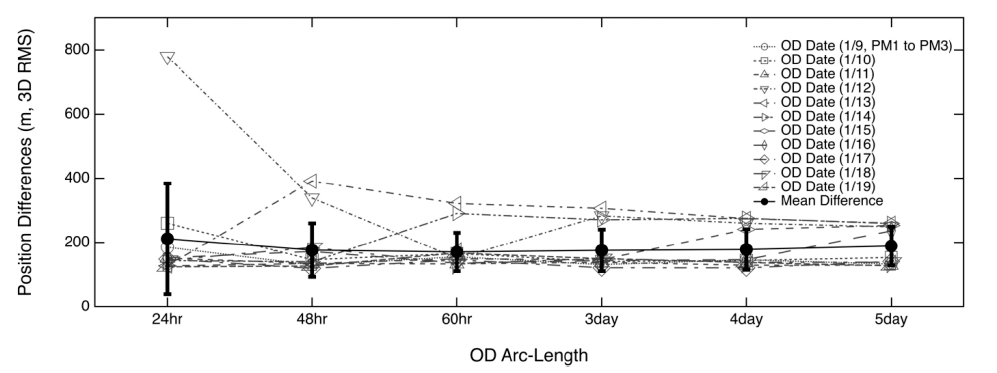
Figs. 7 and 8 show the OD precision (obtained by considering the orbit overlap) and the OD accuracy (obtained by calculating the differences between the true and determined positions), respectively. The mean orbit overlap differences for the 24-hr, 48-hr, 60-hr, 3-day, 4-day, and 5-day arc lengths were of 205.3 m, 136.2 m, 122.8 m, 10.5 m, 87.7 m, and 90.5 m, respectively; moreover, the correspondent standard deviation values were of 223.0 m, 110.4 m, 64.5 m, 3.6 m, 57.1 m, and 59.8 m, respectively. The results of overlap comparison indicate that both the OD precision and stability increased proportionally with the tracking arc duration. Additionally, we found that the overlap precision did not drastically improve for arc length > 4 days. Similar trends were observed from the orbit difference assessments; however, the orbit accuracy remained almost unchanged when using arc lengths > 48 hrs. The orbit differences for the 24-hr, 48-hr, 60-hr, 3-day, 4-day, 5-day arc lengths were of 211.8 m, 176.5 m, 170.6 m, 175.8 m, 178.3 m, and 189.2 m, respectively; moreover, the correspondent standard deviation values were 172.1 m, 83.1 m, 59.8 m, 64.6 m, 63.3 m, and 60.5 m, respectively. All the results are summarized in Table 10. The OD accuracy was lower in the case of the 5-day tracking strategy than for shorter arc lengths; additionally, we noted that longer arc lengths corresponded always to a better performance. Since the 3.5 phasing loop trans-lunar trajectory has an elliptical orbit, the position of the spacecraft on the phasing loops can affect the OD accuracy. In this case, although the OD tracking data become longer, their accuracy may not be improved due to the tracking data around the perigee or apogee. Therefore, longer arcs are not expected to correspond always to better OD accuracies.
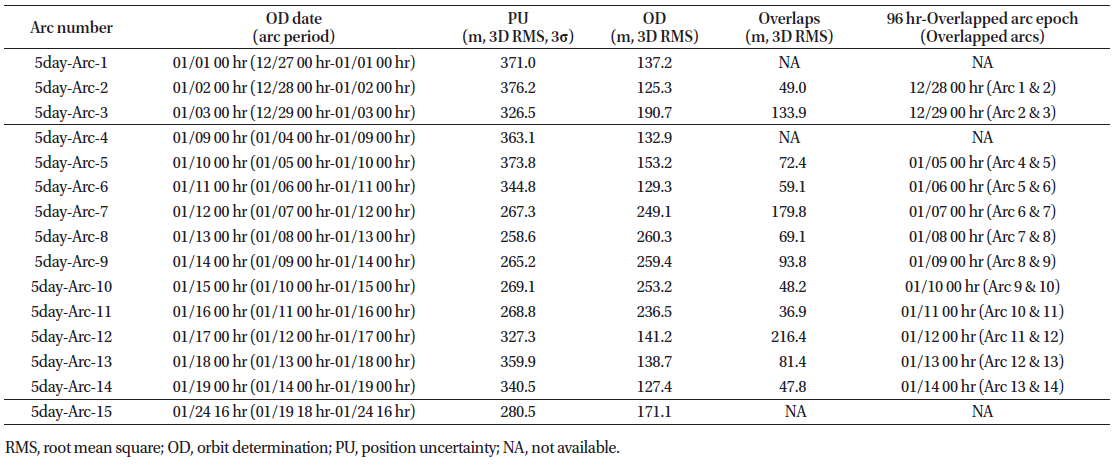
The number of OD arc cases investigated for the PM3– LOI phase is lower than that for the launch–PM1 and PM1–PM3 phases. As shown in Figs. 9–11, the OD results showed similar trends to those observed in other periods; however, fewer OD cases than those before PM3 revealed an indistinct tendency.
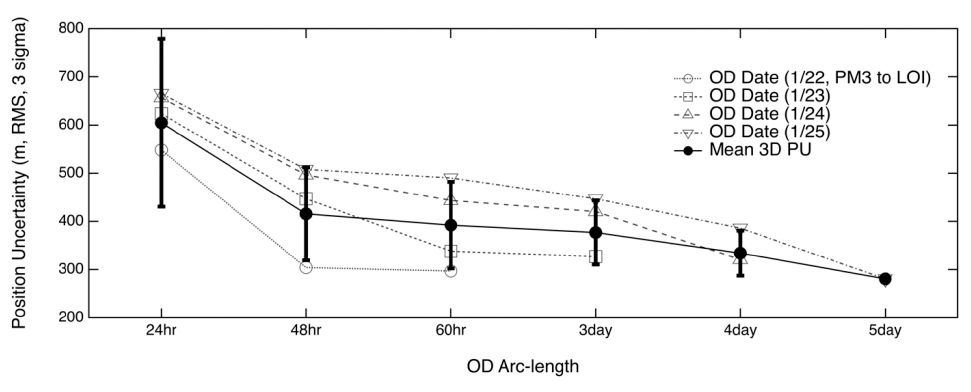
Fig. 9 shows the position uncertainties by error covariance of the OD cases. The detailed results for all arcs are displayed in Tables 3–8. Only one result was obtained for the 5-day OD arc length. The mean values of the position uncertainties were 604.9 m, 415.5 m, 392.0 m, 376.8 m, 334.0 m, and 280.5 m for the 24-hr, 48-hr, 60-hr, 3-day, 4-day and 5-day arc lengths, respectively; moreover, the standard deviations were 174.2 m, 96.3 m, 89.9 m, 66.7 m, and 46.8 m for 24-hr, 48-hr, 60-hr, 3-day, and 4-day arc lengths, respectively. The standard deviation of the 5-day OD arc case was null, since only one value was available. The total position uncertainties obtained for the 5-day and 24-hr arc lengths indicated the highest and lowest precisions, respectively.
Fig. 10 shows the results of the orbit overlap comparison for five arc-length OD cases (no consecutive arcs were observed in the case of the 5-day arc length). The 24-hr arc OD delivered the worst performance, while the other arc settings delivered results with similar precisions. The mean overlap differences were of 373.8 m, 190.7 m, 171.6 m, 207.5 m, and 235.8 m for the 24-hr, 48-hr, 60-hr, 3-day, and 4-day arc lengths, respectively; moreover, the correspondent standard deviations were 262.1 m, 110.0 m, 115.3 m, 95.8 m, and 10.6 m, respectively.
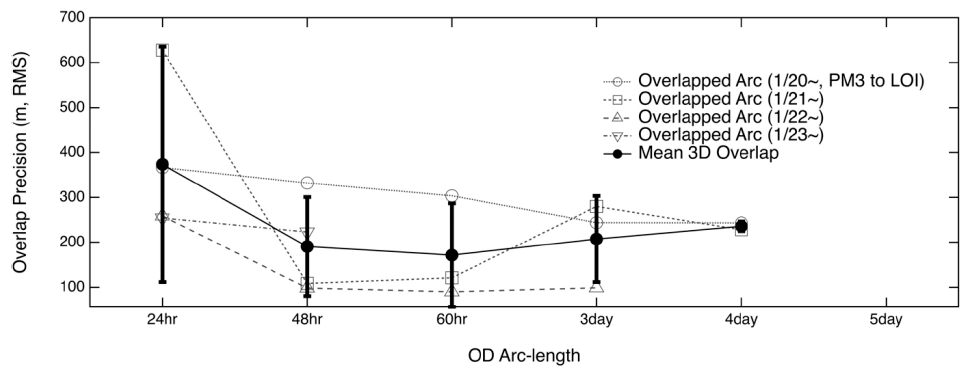
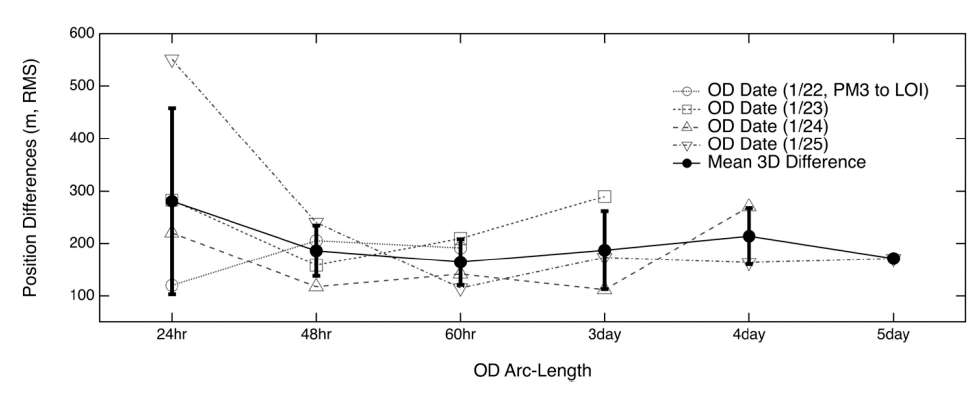
Fig. 11 shows the orbit accuracy based on the differences between the true and estimated orbits. Similar trends were observed for the OD in the case of increasing arc lengths; however, the differences between the length cases were not significant, except in the case of the 24-hr arc length. The mean position differences were of 280.4 m, 185.9 m, 164.3 m, 187.1 m, 213.7 m, and 171.1 m for the 24-hr, 48-hr, 60- hr, 3-day, and 4-day arc settings, respectively; moreover, the correspondent standard deviations were 177.4 m, 48.0 m, 43.6 m, 74.2 m, and 53.4 m, respectively. The biggest difference was reported in the case of the 24-hr arc length, while the best accuracy was reported in the case of the 60 hr-tracking strategy, as shown in Table 11.
In this study, we described the KPLO OD results for the Earth-Moon Transfer phase and investigated the arc-length effect on the OD in six cases (arc-lengths of 24 hrs, 48 hrs, 60 hrs, 3 days, 4 days, and 5 days). We discovered that the OD orbit accuracy was higher in the case of longer arcs; however, unexpected trajectory correction maneuvers, abnormal spacecraft operations, and contingency situations cannot guarantee long arc lengths in the trans-lunar phase. Therefore, an OD analysis that considers various tracking arc lengths is useful for the preparation of actual KPLO mission operations in the Earth-Moon Transfer phase. Our analysis of the arc-length effect on the OD led to three main conclusions: 1) a 24-hr arc length is not suitable for the KPLO OD during the trans-lunar phase, since the orbit precision and accuracy values would be too large and unstable; 2) tracking arcs > 3 days can deliver precise and stable OD results for the KPLO mission; 3) the OD analysis should be conducted by applying various assessment methods. We used three different orbit quality checks, finding that their trends were all very similar; however, the OD performance was different in some cases. Therefore, it is necessary to check the OD precision and accuracy using various evaluation methods. Considering the quick processing of the sequential estimation and the mission operation effectiveness, we recommend a 3-day arc length for the KPLO OD during the Earth-Moon Transfer phase.
5. CONCLUSIONS
In this paper, we presented the results of an OD analysis conducted using a sequential estimation technique for the KPLO mission in the Earth-Moon transfer phase; moreover, we discussed the arc-length effect on the OD. The KPLO will be Korea’s first lunar exploration mission. To ensure a stable operation and the success of the mission during the Earth-Moon Transfer phase, it is critical to perform an OD analysis. To conduct such analysis, we utilized Doppler and range measurements tracked by three ground stations (one of the KDSA and two antennas of the DSN); additionally, the OD quality was assessed by analyzing the position uncertainty, the precision of the orbit overlaps, and the position differences between the true and determined orbits. Six OD arc-lengths cases were considered: of 24 hrs, 48 hrs, 60 hrs, 3 days, 4 days, and 5 days. Among those, the arcs > 3 days demonstrated a stable precision and highly accurate results. Considering the characteristics of the sequential estimation approach and effective mission operation, we concluded that a 3-day OD approach would deliver the most effective performance. This strategy is suitable in the case of stable flight dynamics operations and robust navigation capabilities during the trans-lunar phase of the KPLO. Overall, this study provides useful guidelines and new knowledge regarding the KPLO flight dynamics operations in the trans-lunar phase.













