Early Phase Contingency Trajectory Design for the Failure of the First Lunar Orbit Insertion Maneuver: Direct Recovery Options

Two-body equations of motion of the spacecraft flying in the vicinity of the Moon can be expressed as (Vallado 2013):(1)(2)

where μ is the gravitational constant of the Moon, and r and v denote position and velocity vectors of the spacecraft, respectively. With the initial position (r₀ = r_hyp) and velocity ($v_0=v_{hyp}+\Delta v_{LOI}^{1_{st}}$) vectors, the spacecraft will be captured successfully into the lunar orbit after the first LOI maneuver execution. The terms, r_hyp and v_hyp , denote the hyperbolic arrival position and velocity vectors of the spacecraft at the moment of periapsis arrival. $\Delta v_{LOI}^{1_{st}}$ is the applied first LOI maneuver, assumed as an impulsive burn, to facilitate lunar capture of the spacecraft. If the first lunar brake or execution of $\Delta v_{LOI}^{1_{st}}$ fails due to various reasons during the real operation, then the spacecraft will fly away from the Moon requiring additional trajectory recovery plans. In the early system design and analysis phase, every necessary maneuver to recover trajectory is assumed to be an impulsive burn in further discussions.

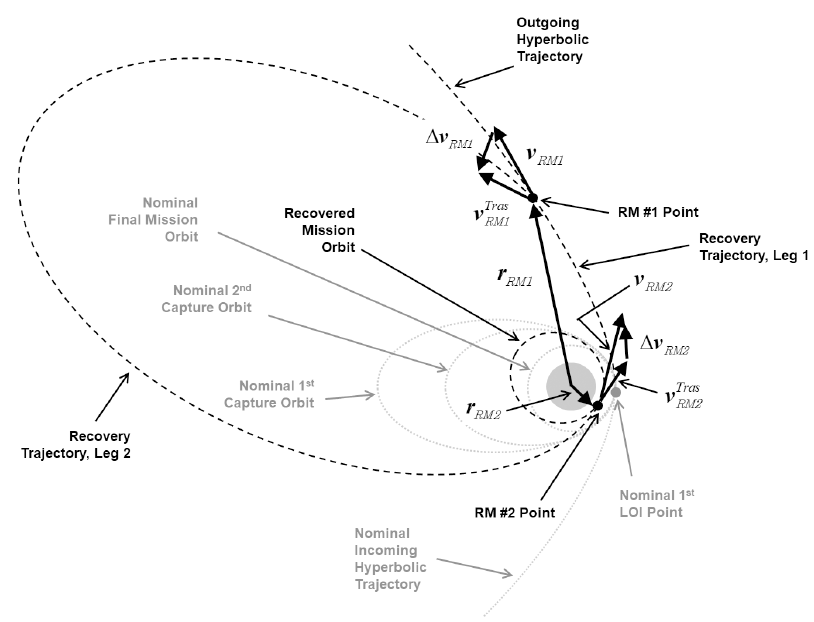
In case of the failure of the first LOI maneuver, the contingency trajectory design problem can be solved by the orbital boundary value problem, finding the trajectory connecting two given points with a flight time. Therefore, at least two additional RMs will be necessary to capture the spacecraft into an orbit around the Moon. Note that these assumptions are only valid within the direct recovery case. The RM #1 will be applied to adjust the trajectory toward the Moon, and the RM #2 will insert the spacecraft into an orbit around the Moon. To solve the orbital boundary value problem, the current work applied the widely known Lambert theory to compute the characteristics of the RMs. Since the first accurate solutions of the Lambert’s problem by Gauss (1857), many authors have devoted their efforts to advancing solutions to Lambert’s problem, including Lancaster & Blanchard (1969), Bate et al. (1971), Gooding (1990), Battin (1999). Among these methods, Gooding’s method was found to be the most stable method when considering numerical stability as well as computational complexity (Izzo 2015). Therefore, the current work adapted the given contingency trajectory design problem into the widely known Lambert theory and solved it with Gooding’s method. To solve Lambert's problem via Gooding's solution, the current work derived both the position and velocity vectors at the moment of the RM #1 execution (r_RM1, v_RM1) and RM #2 execution (r_RM2, v_RM2).

To compute r_RM1 and v_RM1, r_hyp and v_hyp are obtained from r₀ and v₀ with the assumption that r_hyp = r₀ is still valid, as the current work assumed every maneuver to be an impulsive burn. Therefore, v_hyp can simply be computed by:(3)

where M is the state transition matrix that converts states expressed in the inertial frame into the radial-tangentialnormal (RTN) frame with unit vector components of ${\widehat{u}}_r,{\widehat{u}}_t\hspace{0.17em}\text{and}\hspace{0.17em}{\widehat{u}}_n$. In addition, v_r, v_t, and v_n are the periapsis velocity vector components of the approach hyperbolic trajectory, where subscripts r, t and n indicate the radial, tangential, and normal direction of each component. The periapsis velocity vector components may be defined as v_t = v_app and v_r, v_n = 0 where v_app is the magnitude of the hyperbolic approach velocity at periapsis. M can be computed using r₀ and v₀, and these vectors can be obtained directly using the first capture orbit’s six orbital elements (a₀, e₀, i₀, ω₀, Ω₀, v₀), which are all pre-designed parameters. The semi-major axis, a₀, of the first capture orbit can be computed using the desired orbital period of the first capture orbit, P; and eccentricity, e₀, can be derived using the mission dependent radius of the closest approaching periapsis, r_p, as shown in Eq. (4) (Brown 1998).

In Eq. (4), R_m is the mean radius of the Moon, and h_p is the periapsis altitude at the moment of the closest lunar approach, which is also a pre-defined value. Other elements, such as the inclination, i₀, argument of periapsis, ω₀, right ascension of ascending node, Ω₀, and true anomaly, v₀, are mission dependent parameters determined during mission definition or the LOA phase design. After successful derivation of r_hyp and v_hyp, those states are numerically propagated during t_RM1 to find r_RM1 and v_RM1, where t_RM1 is the elapsed time since the first LOI execution time that is nominally planned. Hereinafter, t_RM1 is termed TOF Leg 1. For r_RM2 and v_RM2 computation, the final orbital elements (a_f, e_f, i_f, ω_f, Ω_f, v_f) of the spacecraft, again pre-targeted values for the successful trajectory recovery options, are used directly.

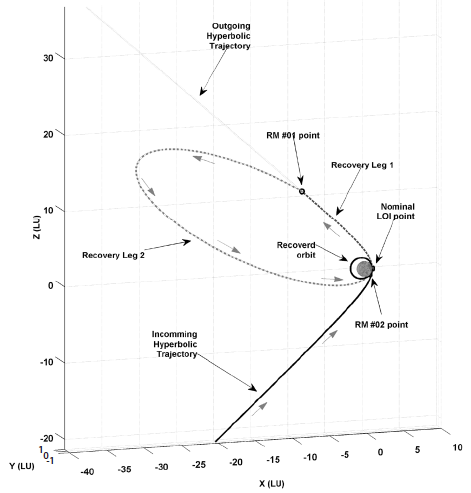
With given values for r_RM1, v_RM1, r_RM2, v_RM2, μ, and t_RM2, the established contingency trajectory design problem can be solved by Gooding's method, where t_RM2 indicates the elapsed time between the execution of RM #1 and RM #2 execution at r_RM2 and is defined as TOF Leg 2 in the following discussions. After solving Lambert's problem using Gooding's method, the initial, $v_{RM1}^{Tras}$, and final, $v_{RM2}^{Tras}$, velocity vectors of the recovery trajectory can be obtained and, with simple mathematics, the required velocity changes for both RMs, Δv_RM1 and Δv_RM2, can be determined. For more details on Gooding’s solution procedure for Lambert’s problem, i.e., the kinematic geometry, iteration process, flight-time, and velocity computation algorithms, including the FORTRAN subroutine code, readers may refer to the work done by Gooding (1990). In Fig. 1, the corresponding geometry of the RM executions is depicted.

Fig. 1. Geometry of recovery maneuver execution (not to scale).

Download Original Figure

As previously discussed, the current study focused on establishing a contingency trajectory design strategy for the early mission design phase; therefore, two-body equations of motion were used, and every necessary burn to recover trajectory was assumed to be an impulsive maneuver. To integrate the equations of motion, the numerical integrator function of “ODE113” provided by MATLAB® is used. During the solution of Lambert's problem via Gooding's method, the following additional constraints are considered. The lower and upper boundary conditions are given as 1 to 24 hours for t_RM1 and 1 to 30 days for t_RM2, and those durations are equally divided into 100 steps to search for the best solutions to minimize the overall RM magnitudes defined as |Δv_RMs | = |Δv_RM1|+|Δv_RM2| . These conditions indicate that RM #1 is executed within at least 1 to 24 hours after the nominal first LOI burn failure, and RM #2 is executed within 1 to 30 days after the execution of RM #1. The sum of t_RM1 and t_RM2 can be regarded as the total flight time, ΔtTOF, required to recover the trajectory. The selected boundaries are given from numerous trials during the simulations. Among the recovery trajectory solutions obtained, those solutions having spacecraft-Moon distances more than 64,000 km, the lunar sphere of influence distance, are automatically rejected to focus on two-body dynamics. To compute r_hyp and v_hyp, the following conditions are used. For r_hyp computation, r₀ is computed by using the predefined first nominal capture orbit conditions: i₀ = 90° with ω₀, Ω₀, and v₀ set to 0°. The other orbital elements, a₀ and e₀, are determined from the pre-defined v_app, P, and h_p. P is assumed to be 12 hours, and h_p is given as 100 km in altitude above the lunar surface. For v_hyp derivation, v_app is assumed to be about 2.497 km/s, which is the current estimate of the hyperbolic velocity magnitude at periapsis approach for nominal KPLO trajectory design results. The current study proposed the possibilities of two different recovery cases, insertion into circular mission orbit (hereinafter Case 1) and insertion into elliptical mission orbit (hereinafter Case 2), within the direct recovery options. The two recovery cases differ from each other by the shape of the mission orbit after recovery. The Case 1 recovered mission orbit has a circular shape with h_p of 30, 50, 100, 200, 500, and 1,000 km. Case 2 has a slight modification of the recovered mission orbit’s shape with elliptical orbits having h_p of 30, 50, and 100 km. The current work analyzed Case 2 to investigate feasible recovery options that can be achieved within the boundaries of the current fuel budgets for the KPLO mission while partially performing its scientific mission after recovery. To compute v_RM2 for each case, a circular orbit with if = 90° and ω_f, Ωf, and vf set to 0° is used for Case 1 with the derivation of P consistent with given altitudes of h_p. For Case 2, shape as well as the orientation of the recovered mission orbit is changed to an elliptical orbit with ω_f = 45°, with other orbital elements the same as in Case 1 except for af and e_f. a_f and e_f are derived according to the possible delta-V margins allocated to the KPLO mission with the assumed h_p values for Case 2. By properly changing ω_f for the recovered mission orbit, it is expected that KPLO may partially pursue its scientific mission after a successful recovery, though it will be limited. In Table 1, the characteristics of the two recovery cases are summarized.

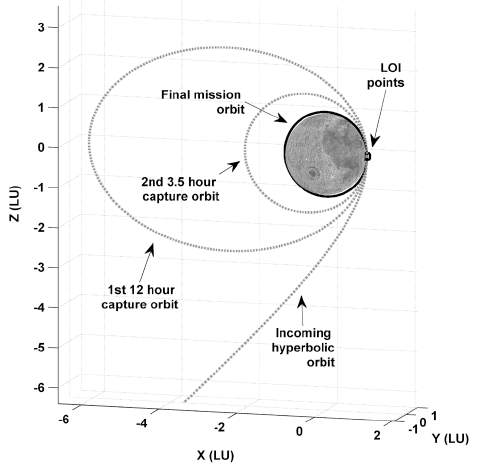
Before discussing the recovery options obtained from the current work, the nominally planned capture sequence for the KPLO mission, including the delta-Vs magnitudes for each LOI burn, is briefly summarized. This is intended to give the background for the nominal capture sequence currently planned for the KPLO mission and to provide insights into the following analysis of the results. During the LOA phase, the KPLO will be inserted into its final mission orbit by establishing a two phasing loop orbit around the Moon after the arrival of the periapsis by a hyperbolic approach. The first and second capture orbits will have orbital periods of about 12 hours and about 3.5 hours, respectively, and the KPLO will be placed into its mission orbit, a polar circular orbit at an altitude of 100 km with an orbital period of about 118 min. The current estimate of nominal periapsis hyperbolic approach velocity, v_app, is found to be about 2.497 km/s. It is assumed that two-body equations of motion are used and every phasing orbit’s periapsis altitude as well as the altitude of the mission orbits (100 km) are the same. This allows the periapsis velocity for each phasing loop orbit as well as the circular velocity of the final mission orbit to be derived by using pre-defined periods for each orbit. As v_app is already known, the required delta-Vs for each LOI burn can be easily determined. The expected event sequences for the LOA phase are summarized in Table 2; however, note that the sequence and associated values are only valid for the early stage mission design and analysis phase and may differ from sophisticated trajectory design results using N-body dynamics with finite burn maneuver models. As shown in Table 2, the sum of all LOI magnitudes, the expected overall delta-Vs for the LOA phase, is found to be approximately 863.064 m/s. Note that this 863.064 m/s of delta-V is an ideal value that is required only for the LOA phase except for the delta-V required for the trans lunar injection (TLI) burn. In addition to the ideal delta-Vs for the LOA phase, maximum delta-Vs of about 200 m/s are additionally allocated for the total delta-V budget for the KPLO mission, including launch window extension, launcher dispersions, midcourse correction maneuvers (MCC), system margins, etc. Overall delta-Vs of about 1.063 km/s can further be utilized for recovering the trajectory, even if the original mission life time may be shortened. Fig. 2 shows the nominally planned capture and mission orbits for the LOA phase.

Fig. 2. Nominally planned LOA phase orbit (1 lunar unit (LU) = 1,738.2 km).

Download Original Figure

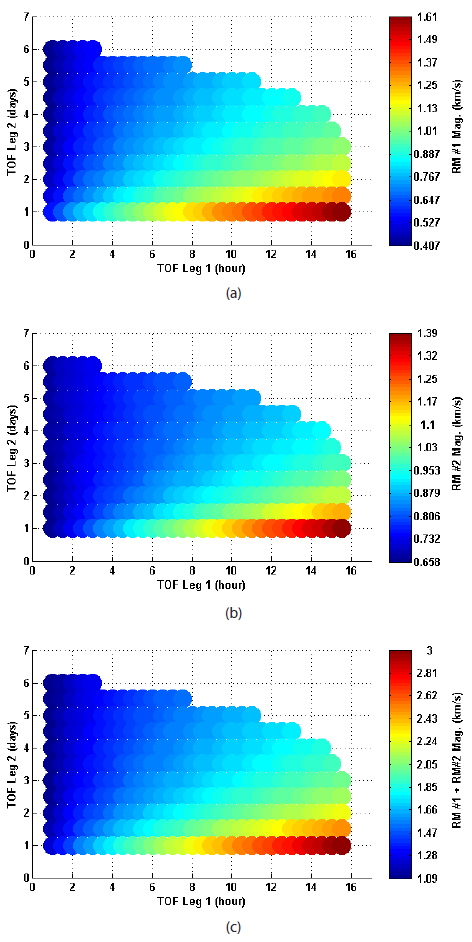
As already discussed, Case 1 assumes that the recovered mission orbit is a circular orbit with different h_p of 30, 50, 100, 200, 500, and 1,000 km. To search for the best execution time for RM #1 and RM #2 that minimize the magnitudes of the RMs (the best TOF Leg 1 and TOF Leg 2). As a result, a quicker execution of the first RM after the failure of the first LOI plays a significant role in reducing the overall magnitudes of the RMs. However, it is concluded that the TOF Leg 1 should be within the boundaries of 4.0 to 6.0 hours and the TOF Leg 2 from 5.0 to 5.5 days regardless of the recovered circular orbit’s altitude. To arrive at these conclusions, system engineering and ground operation aspects, such as the considerable amount of time required for precise orbit determination, mission planning, and command generation validation, etc., are considered. In Fig. 3, the characteristics of the required RM magnitudes as a function of TOF Leg 1 and TOF Leg 2 for a 100 km circular orbit recovery case are shown. As shown in Fig. 3(a), it is clear that RM #1 should be executed as soon as possible if the first LOI burn is a failure. However, during the real operation, a considerable amount of time is necessary, at least several hours or more for RM #1 execution. This is to obtain knowledge of the spacecraft’s exact orbital status as well as to plan and validate further recovery options. For TOF Leg 2, the magnitude of RM #2 is strongly influenced by the TOF Leg 1. For the same TOF Leg 1 conditions, spending more time for Leg 2 mostly requires less delta-Vs for RM #2 as shown in Fig. 3(b). The characteristics of the required overall delta-V magnitude for the RMs are depicted in Fig. 3(c).

Fig. 3. Required RM magnitudes ((a) RM #1, (b) RM #2, and (c) overall RMs) as a function of TOF Leg 1 and TOF Leg 2 for a 100 km circular orbit recovery case.

Download Original Figure

A summary of the minimum and maximum RM magnitudes for different orbit altitudes is shown in Table 3 when TOF Leg 1 is selected to be from 4.0 to 6.0 hour and TOF Leg 2 from 5.0 to 5.5 days. As shown in Table 3, the required magnitude of RM #1 is increased with an incremental increase in the target altitude of the recovery orbit, though the increment is very small. Unlike the RM #1 magnitude tendency, the magnitude of RM #2 is greatly reduced with an incremental increase in the recovery orbit’s target altitude. The RM #2 magnitude decrease can be understood by the fact that the approach velocity of the spacecraft at the moment of the RM #2 execution point gets smaller with the incremental increase in target altitude. Although the required overall magnitude of the RMs decreased with an incremental increase in the target altitude of the recovered circular orbit, the required overall RM magnitude to recover the mission orbit still exceeds the overall delta-V budget allocated for the KPLO mission including margins of about 1.063 km/s. Therefore, it can be concluded that the recovery strategy shown here can never be achieved under the delta-V budget currently allocated for the KPLO system design. In Fig. 4, an example recovery trajectory is shown for the case of direct insertion into a 100 by 100 km circular polar orbit. To plot this example, TOF Leg 1 and Leg 2 are selected to be 4.0 hour and 5.0 day, respectively, and the required overall RM magnitude is found to be about 1.377 km/s.

Fig. 4. Example recovery trajectory. Direct insertion into a 100 km by 100 km circular polar orbit case. TOF Leg 1 and Leg 2 are selected to be 4.0 hour and 5.0 day, respectively.

Download Original Figure

In the previous section, it is concluded that the Case 1 recovery option is not achievable within the currently allocated delta-V budget for the KPLO system design. Therefore, this sub-section discusses recovery options that can be possible within the delta-V budget currently allocated. A slightly different approach is used during the simulation to enforce the overall magnitude of the RMs used during the recovery. The overall magnitude of the RMs is intentionally adjusted to not exceed the value of the nominally planned overall magnitude of the delta-Vs (about 0.863 km/s) allocated for the KPLO LOA phase. Both RM #1 and RM #2 are derived by solving the Lambert problem as in Case 1, and the magnitude of RM #2 is replaced with a value that is recalculated using nominally planned and derived RM #1 magnitudes. By applying this strategy, the shape of the recovered orbit will no longer be circular but will be elliptical. With this approach, candidates for recovered mission orbits that can be achieved within the allocated delta-V budget can be investigated. As a result, the achievable orbital shapes using this approach are summarized in Table 4 with respect to different periapsis orbit altitudes after successful recovery. For this simulation, TOF Leg 1 is bounded within 4 ~ 6 hours and TOF Leg 2 within 5 ~ 6 days. Note that the values shown in Table 4 are the averages of all the candidates obtained.Table 5Table 6

As shown in Table 4, regardless of the periapsis altitude of the recovered mission orbit, it is found that about 0.655 km/s of RM #1 is required to adjust the trajectory toward the Moon. Therefore, slightly more or less than 0.200 km/s of velocity change can be allocated for the RM #2 execution. With about 0.200 km/s for RM #2, the achieved shape of the final recovered mission orbit is too elliptical to perform the scientific mission of the KPLO mission originally planned. For example, the orbital altitude at the moment of north- and south-pole approach is found to be about 1,137.778 km when the periapsis altitude is targeted to be 30 km. If the targeted periapsis is greater than 30 km, then the north- and southpole approach altitude is also higher than 1,137.778 km. Note that the current work is performed under the condition that the spacecraft’s closest approach point to the Moon from recovery Leg 2 is located near the lunar equator, indicating that the location of the RM #2 execution as well as the periapsis of recovered orbit is near the lunar equator. With a highly elliptical recovered mission orbit having periapsis located near the lunar equator, most of the nominally planned scientific mission of the KPLO cannot be performed with the associated payloads, as their design basis indicates operation at 100±30 km or slightly more above the lunar surface. The operation ranges of the LUTI can be very limited to the flight times when altitudes are near the 100 km range. For the ShadowCam operation, results would be almost meaningless when flight altitudes of the near polar-regions are more than 1,000 km.

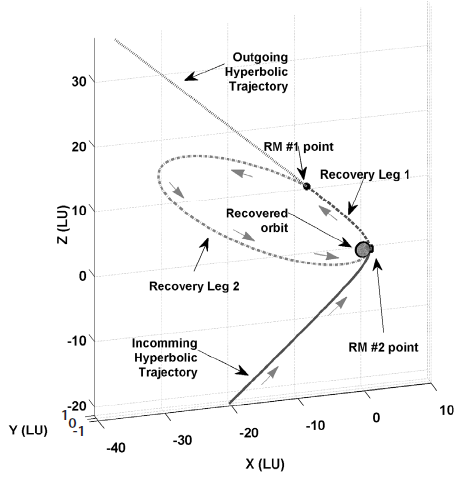
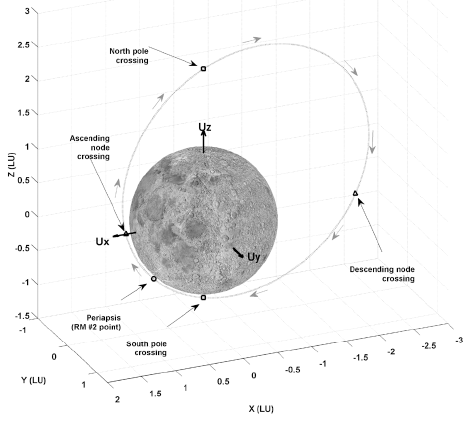
One of the alternative solutions for maximizing the scientific information obtained in the contingency situation is the adjustment of the recovered orbital shape to match the originally planned flight requirements insofar as possible. As an example, if the sub-spacecraft point at the periapsis passage (the RM #2 execution location) is adjusted and its altitude lowered, then the operation ranges of LUTI may expand even with the elliptical shape of the mission orbit. There could be some candidate elliptical mission orbits in which ShadowCam can be operated partially to either cover lunar south or north poles. In addition, such an orbit adjustment could benefit the quality of the KMAG measurements as the flight altitude is much lower than the altitudes nominally planned. In Tables 5-7, the expected orbital shape of the recovered orbit is summarized. To derive the results shown in Tables 5-7, the periapsis altitude of the recovered orbit is adjusted to 30, 50, and 100 km, and -45° of AoP is given to locate sub-periapsis points near -45° of latitude on the Moon to maintain low altitudes at the poles. Unlike the results shown in Table 4, the delta-V magnitude for RM #2 is limited to 0.863 km/ s and also to 0.963 and 1.063 km/s to include 100 and 200 m/ s of mission redundancy delta-Vs to determine their effect on the shape of the recovered mission orbit. The TOF for Leg 1 and Leg 2 shown in Tables 5-7 are selected to be 5.00 hours and 5.25 days, respectively. As shown in Tables 5-7, the altitude of the spacecraft at the lunar south-pole passage is much lower than those values in Case 1, though the north-pole passage altitude is greatly increased, which certainly is helpful to the ShadowCam operation during the south-pole passage. Another benefit from the current finding is that the spacecraft maintains an almost constant altitude from the south-pole passage to the ascending node crossings. This will help establish the payload operation plan during the flight above these regions and efforts to calibrate the collected payload data. Regarding RM #2 magnitude, the use of more delta-Vs in RM #2 lowered the overall altitude of the recovered mission orbit, but with very trivial results. As an example, for the case when the periapsis altitude is given as 30 km (shown in Table 5), the lunar south-pole passage altitude is reduced to 271.473, 219.54, and 170.114 km when 0, 100, and 200 m/s of allocated system delta-V margins are additionally applied to RM #2 during the recovery. Current findings show that adjusting the periapsis altitude as low as possible with the use of every possible delta-V margin to RM # 2 may result in one candidate recovered orbit that may partially pursue the scientific mission after successful recovery. In Fig. 5, an example of such a recovery trajectory is shown for the elliptical mission orbit insertion case with AoP of -45° and 30 km of periapsis altitude. Fig. 6 is a zoomed-in view of the recovered mission orbit shown in Fig. 5. To scale the coordinates in both Figs. 5 and 6, note that a lunar unit (LU) (1 LU = 1,738.2 km) is used, and Ux, Uy, and Uz shown in Fig. 6 denote the unit vector components of the Mooncentered inertial frame.

Fig. 5. Example recovery trajectory. Insertion into elliptical mission orbit with AoP -45° and 30 km of periapsis altitude.

Download Original Figure

Fig. 6. Zoomed view of recovered elliptical mission orbit. Case with AoP of -45° and 30 km of periapsis altitude.

Download Original Figure