1. INTRODUCTION
It is well known that the ionospheric conditions significantly affect high frequency (HF) communication and the accuracy of single channel Global Positioning System (GPS) receivers. Ionospheric conditions can be monitored by observations of total electron contents (TEC) using a network of two channel GPS receivers. The two-dimensional computerized ionospheric tomography (CIT) was firstly suggested by Austen et al. 1988, showing the possibility of converting measured TECs into vertical electron density profiles. The fundamental concept of CIT is to use the observed slant TEC (STEC) as the sum of path lengths of GPS signal through specific voxels multiplied by the electron density of the voxel. The concept of CIT includes uncertainties originated from the observed STEC and the inversion calculation. Therefore, a number of studies proposed various tomographic methods to mitigate difficulties in solving the ill-conditioned inverse problem. (Raymund et al. 1990;Kunitsyn et al. 1994;Raymund 1994, 1995;Pryse et al. 1998).
The quality of CIT in the ionosphere depends critically on the number of GPS STECs that are measured along the path between ground receivers and GPS satellites. The more passes of GPS satellites through the voxels over the region of interest, the better results from CIT are expected. However, there are significant portion of the voxels in three-dimensional (3D) space which are not crossed by the observed GPS signal paths, making the inversion calculation an ill-conditioned problem. By applying empirical orthonormal functions (EOFs), this ill-conditioned problem could be regularized by reducing the number of unknowns, thereby overcoming the lack of number of signal paths through the voxels. The EOF method has been used in various fields, such as image processing, and EOFs can be derived numerically from singular value decomposition (SVD) of a matrix representing data (Andrews & Patterson 1976;Björnsson & Venegas 1997;Shnayderman et al. 2006). Previous studies have shown that the EOF method can be applied successfully to the ionosphere tomography (Zhao et al. 2005;Lin et al. 2014;Chen et al. 2015). The EOF method allows not only to regularize the inversion problem, but also to save computing time significantly.
In this study, we have developed a computer code based on CIT that computes efficiently 3D electron densities from GPS TEC data 10 min interval over South Korea. The results of CIT are verified with NmF2 measured by inosondes in Icheon and Jeju and also with vertical TEC (VTEC) measured by GPS observations at the center of South Korea. Because the code uses 10 min interval data, the monitoring of the ionosphere over South Korea is enabled almost in real time.
2. DATA
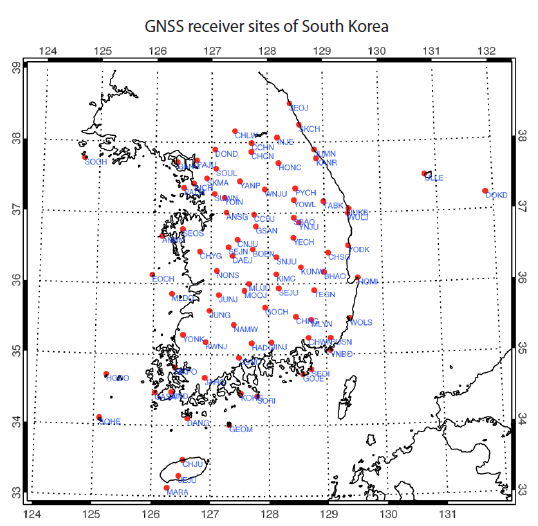
We have used STEC data measured from about 80 GPS stations in South Korea, distributed as shown in Fig. 1. In Japan, the GNSS Earth Observation Network System (GEONET) provides a large volume of STEC data from more than 1,000 GPS receiver sites in Japanese islands. Since the GEONET data are delivered a day after the measurement, they are not appropriate for the near real time tomographic calculations of the ionosphere over Korea. On the other hands, Korea Astronomy and Space Science Institute (KASI) provides STEC data on a 10 min interval by collecting GPS signal data from each operating institute, which is suitable for near real time monitoring of the ionosphere over the Korean peninsula.
Previous studies have described methods to estimate STEC from dual-frequency GPS measurements (Klobuchar et al. 1994;Kohl et al. 1996). By using differential code biases (DCBs) of satellites and receivers, we can calculate STEC as follows:
where STEC is expressed in unit of TECU 1016 electron/m2 and constant K =9.5196. RP2 and RC1 are calculated by using the information of P2 (L2 pseudo-range using the P code in meters), C1 (C/A pseudo-range on L1 in meters) in receiver independent exchange format (RINEX) files and DCB of South Korean receiver (Choi et al. 2011, 2013) and GPS satellites. Satellite DCB are obtained from Center for Orbit Determination in Europe (CODE) at Astronomical Institute of the University of Bern (AIUB). To avoid the effect of outliers in the observations, we limited the elevation angles of GPS rays to higher than 20° at first and then removed 2.5 % of the lowest and highest of each STEC data set. Fig. 2 shows the example of the removal of outlier STEC data which have been observed from 03:00 UT to 03:10 UT on DOY 265 in 2015. Each plus symbol indicates a STEC value. Some values were very high and others were close to zero even though the elevation angles were limited to higher than 20°. It might be due to observational errors such as interruptions of signal from external sources. The blue symbols indicate an STEC values within ±47.5 % of the median of the total data observed on a 10 min interval, while the red symbols indicate the values outside the 95 % range. After the reduction process, the number of STECs used for the CIT analysis is a few thousands, which is performed every 10 min.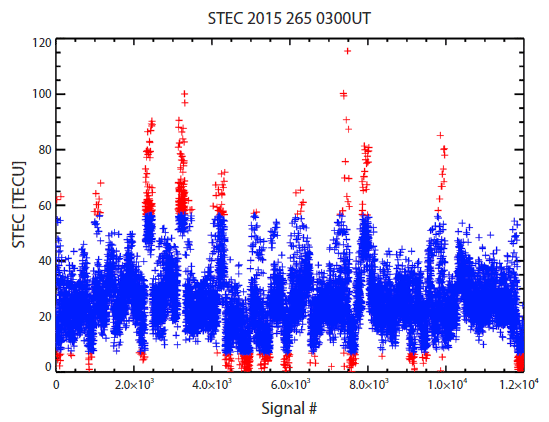
In order to validate the results of the ionospheric tomography, we have used the ionosonde data from Icheon (37.14°N, 127.54°E) and Jeju (33.43°N, 126.30°E) in South Korea provided by Korea Space Weather Center (KSWC) of National Radio Research Agency (RRA). Both stations operate the ionosonde, DPS-4D (Lowell Digisonde international, USA) model. The data are analyzed using ARTIST 5002 software and provided as standard archiving output (SAO) format. The processed data can be downloaded from the web site of KSWC (https:// spaceweather.rra.go.kr/observation/service/iono) as SAO format file. Using the SAO-X software which is provided by University of Massachusetts Lowell Center for Atmospheric Research (UML CAR), we have obtained the ionogram from the SAO file. The KSWC also provides Anyang ionosonde data (37.39°N, 126.95°E), but the measurements at Anyang station was stopped in 2009. The ionosonde data analyzed through ARTIST 5002 software show confidence level from 11 (highest confidence) to 55 (lowest confidence). In this study, we have used only the reliable data with the confidence level of 11 to 33.
We have also used geomagnetic activity index, Kp, from OMNI-2 Web service site (https://omniweb.gsfc.nasa.gov/ form/dx1.html) which is based on the measurements of wind and Advanced Composition Explorer (ACE) satellites.
3.COMPUTERIZED IONOSPHERIC TOMOGRAPHY (CIT)
The CIT algorithm starts with constructing the geometry matrix that relates electron density of each voxel to the STEC dataset. The geometry matrix consists of path lengths along which the GPS signal paths intersect through voxels. Next, we derive EOFs for vertical electron density profiles from the climatology model of (IRI-2016). A linear combination of a few EOFs represents a vertical profile which significantly reduces the number of unknowns to a few unknown coefficients of the combination in the matrix relation between STECs and voxel densities. The reduced matrix relation is then inverted by multiplicative algebraic reconstruction technique (MART). By applying the results of inversion back to EOFs, the electron densities of all the voxels are computed. Finally, the altitudinal smoothing in horizontal direction is performed to obtain regularized ionospheric structure over the region. Details of each stage are described in the following sub-sections.
The ionosphere considered in this study includes a three dimensional space over the latitude of 20°N - 50°N, the longitude of 120°E - 150°E, and the altitude of 90 - 1,000 km. Within this space we set up regular voxels (volume pixels) with a horizontal size of 1° in longitude and latitude and a vertical size of 10 km. The observed STEC can be defined as integrated electron densities, Ne, along the GPS signal path from a GPS satellite to a receiver in the unit of TECU. The STEC can be approximated as the sum of multiplication of path length by electron density of each voxel along the GPS signal path, assuming a constant electron density in each voxel. In matrix form, the i-th observed STEC, bi, can be expressed as:
where m is total number of voxels, aij indicates a length along which i-th GPS ray passes through j-th voxel, xj is the electron density at j-th voxel and ei is the error of measurement and approximation (Das & Shukla 2011; Ssessanga et al. 2015). The matrix, aij, is commonly called as a geometry matrix since it contains geometric information on the rays for the defined voxels. The elements of the geometry matrix for GPS rays can be computed with the subtending angle between the entry and exit points through a voxel in spherical geometry, where the angle is defined between two position vectors emanating from the center of the Earth. Each GPS ray determines a plane that a receiver and a GPS satellite construct along with the center of the Earth. Once the plane is determined, the longitudes, latitudes and altitudes of the entry and exit points through voxels can be computed. The path lengths through each voxel along the ray can then be calculated from the 3D coordinates of the entry and exit points, constructing a row of the geometry matrix. We have developed a code computing the geometry matrix, which has been verified extensively with various GPS signal rays over South Korea.IRI has been developed and continuously improved by a group of International Union of Radio Science (URSI) and the Committee on Space Research (COSPAR) (Bilitza 2001;Bilitza & Reinisch 2008;Bilitza et al. 2014). As an empirical model, IRI strongly depends on observed data sets, but has merits of fast computation as well as independence of heuristic theories. Therefore, IRI has provided an initial condition or reference values of ionospheric models and other applications, including the CIT reconstruction (Huang et al. 1996;Arikan et al. 2007;Ssessanga et al. 2015). The latest IRI, IRI-2016 which was released in Feb. 2016, utilizes the hmF2 model based on constellation observing system for meteorology, ionosphere, and climate (COSMIC) developed by Shubin 2015, as an update from IRI-2012 (Bilitza et al. 2016). The COSMIC observation data set could improve the accuracy of IRI-2016, which was thus adopted as an initial condition of our CIT reconstruction.
Tomography reconstruction of the ionosphere involves the inversion of Eq. (2), which is severely under-determined problem since the number of measured STECs is much smaller than that of the unknowns, xj, the electron density of a 3D voxel. To reduce the number of the unknowns, the vertical profiles of the ionosphere are approximated as a linear combination of a few dominant orthonormal functions which are extracted from a specific large dataset (Howe et al. 1998;Gao & Liu 2002). The orthonormal functions can be derived by carrying out SVD of a large dataset of vertical profiles, constructing a set of EOFs. The SVD technique has been widely used in various fields, and extracting EOFs from a specific data matrix (Xm×n) is well known (Björnsson & Venegas 1997), as follows:
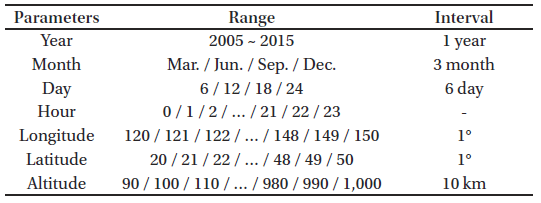
where the singular values are contained in the diagonal matrix Σ, and EOFs are in the U matrix. A standard mathematical package gives the largest singular value at the top row of Σ, and the second largest at the second row, and so on. Thus one can choose the dominant EOFs by evaluating the percentage of contribution of each EOF from the singular values.In order to derive EOFs for the ionospheric vertical pro-files, we have generated 169,136 hourly profiles from the IRI-2016 model with parameters as summarized in Table 1. The hourly IRI profiles cover various solar and magnetic activities and seasons over South Korea. The generated electron density profiles can be expressed as a matrix, Xm×n in which m is the vertical voxel number (92) and n is the number of vertical profiles from IRI-2016 (169,136). After applying SVD to the data matrix, we have chosen only the three largest EOFs from the U matrix. Computing EOFs at each hour is needed because the electron density profile varies with local time. The three EOFs shown in Fig. 3 can represent more than 93 % of the original density profiles. The percentages of the EOFs were computed by summing the matched number of singular values in Σ matrix. The percentages of the three largest EOFs at each hour are summarized in Table 2. As expected from the local time variations of electron density profiles, Fig. 3 clearly indicates different shapes of EOFs at four representative cases. The EOFs mostly show the maximum amplitudes below the altitude of 400 km and the amplitudes decrease with altitude. Furthermore, the EOFs have negative values and this can cause negative values of transformed electron density and geometry matrices by using the EOFs. By using the three largest EOFs from the 92 vertical bins, we reduced the number of the unknowns, whose horizontal range is 31° longitudes by 31° latitudes, from 88,412 (31×31×92) to 2,883 (31×31×3).
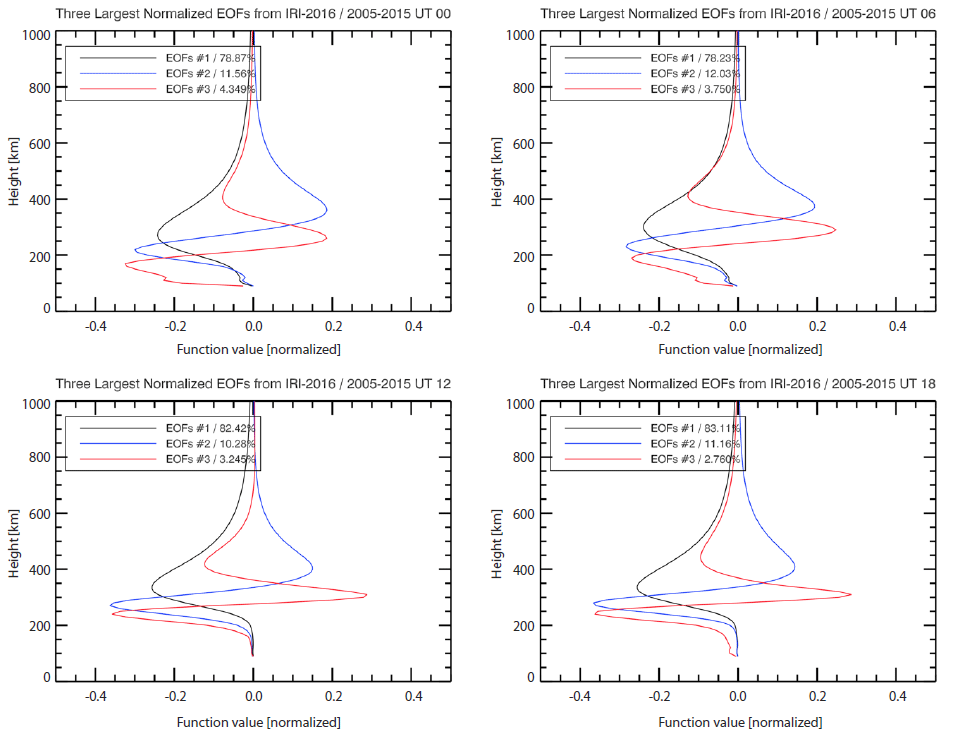
Although we have reduced the number of the unknowns by using three largest EOFs, the significant portion of voxels may still not be intersected by the GPS signal paths. To overcome this limitation, iterative methods like algebraic reconstruction technique (ART) and MART have been suggested in several studies (Raymund et al. 1990;Raymund 1995;Pryse et al. 1998). Especially, MART, a modified version of ART, finds the solution using ratio between an initial guess and calculated values. The MART algorithm is expressed as follows:
where Xjk is the k–th iterated electron density solution and λ is a relaxation parameter (Kunitsyn & Tereshchenko 2003).
In matrix expression, Eq. (2) can be transformed using EOFs, assuming the errors insignificant, as follows:
where E matrix is the EOFs from the U matrix of Eq. (3), c is the extracted number of the EOFs (3×31×31, since three EOFs were chosen for each horizontal grid), H matrix is the transformed geometry matrix and Y is the transformed electron density matrix. The total number of observed ray path i is not changed but the dimensions of the geometry matrix and electron density matrix are reduced. Applying Eq. (6) to the MART algorithm, Eq. (4) can be converted into Note that the elements of H and Y matrices can be negative values because of the EOF transform. Accordingly, we take absolute values of H in the exponent to prevent divergence of the computation. The relaxation parameter, λ', was changed to 0.01 in this study from 0.2 in previous study (Pryse et al. 1998). The termination condition of MART was set as two cases: (1) the relative update value, is less than 1.0 (less than 1 %) or (2) the relative update value increases. Once the conversion of MART iteration reached to the above termination condition, the normal electron density matrix was computed by transforming back to as a solution to CIT.Thus far, we assumed that all electrons are contained in the altitude range between 90 and 1,000 km. However, electron contents in the plasmasphere are not negligible because the measured GPS signals pass through the plasmasphere up to the altitude of 20,200 km. Lee et al. (2013) showed a significant amount of the plasmaspheric TEC (PTEC) above 1,336 km, at which the GPS receiver on board Jason-1 satellite measures TEC between Jason-1 and GPS satellites. The PTECs at middle latitudes are approximately constant over varying local time, season and geomagnetic activity. We revised the observed STEC at the ground by removing PTEC as follows:
A constant value of PTEC was taken as 3 TECU and the elevation angle of the GPS signal ray (elev) was considered. In this way, the plasmaspheric STEC was removed and the revised STEC was used for our CIT analysis over South Korea.
When the number of GPS rays is insufficient to intersect all the voxels, the information conveyed from the GPS ray via the EOFs may not be linear since the EOFs show large amplitude below 400 km. In other words, the transformed electron density matrix, Y, is strongly affected by the GPS ray penetrating the lower altitude region, while the higher altitude intersection point can only have a little effect on the vertical profile. This limitation may cause an artificial discontinuity in the reconstructed ionospheric density. In order to mitigate the defect due to the insufficient number of the GPS rays used, we have performed horizontal smoothing over 5 voxels for each altitude plane at the last step of CIT.
4. RESULTS
Fig. 4 shows an example of comparison between the initial guess from IRI-2016 and the CIT result at 03UT on DOY 265 in 2015. On this day, the geomagnetic activity was low and it was the noon local time (UT = LT - 9). The number of GPS signal rays used was about 9,000, whose mean vertical TEC (VTEC) was 19.2 TECU over South Korean sector (35°N-40°N, 125°E-130°E). The observed VTEC includes electrons between the ground and the GPS satellites while the VTECs from IRI-2016 and CIT were calculated only up to 1,000 km in altitude. Therefore, we removed the plasmaspheric VTEC of middle latitude region, 3 TECU, from the observed VTEC to compare with the VTECs of IRI-2016 and CIT. The mean VTEC of IRI-2016 over South Korean sector was 24.9 TECU, indicating that IRI-2016 overestimated electron density in this example. On the other hand, the mean VTEC of the CIT result over South Korean sector was 17.2 TECU, which is closer to the revised GPS VTEC, 16.2 TECU. The black lines in Fig. 4(a) indicate GPS signal paths used for the CIT. Figs. 4(b) and 4(c) show TEC maps of IRI-2016 and the CIT, respectively, along with GPS signal paths. In the region covered by the GPS rays, the CIT VTEC was significantly different from the IRI VTEC.
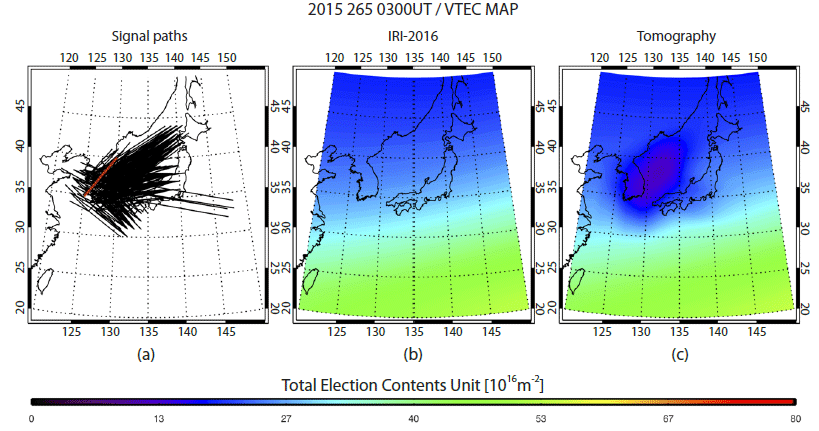
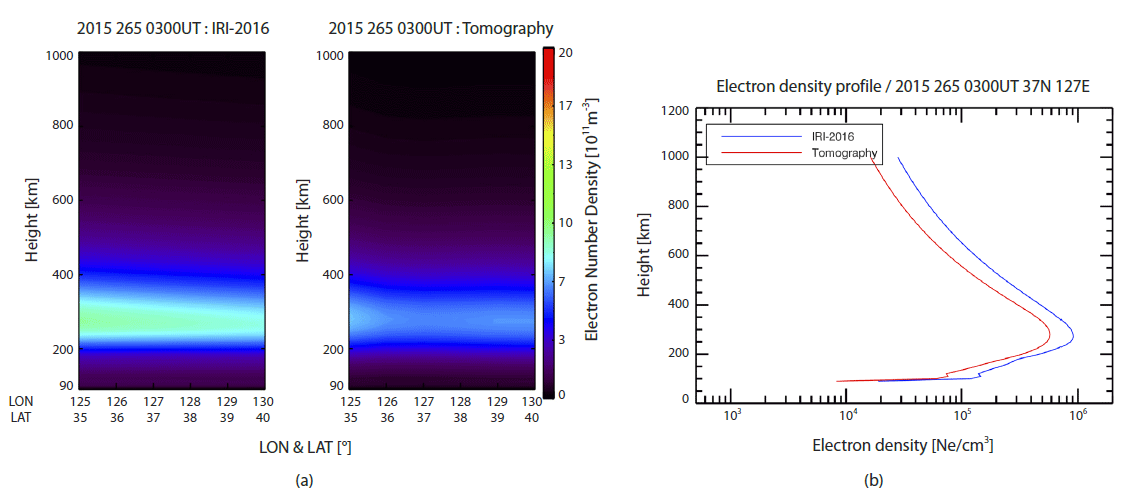
Fig. 5(a) exhibits two-dimensional ionospheric electron density structure along the red line marked on Fig. 4(a). The 2D structure of the CIT results changes quite significantly from the initial guess of IRI especially around the F2 peak. Fig. 5(b) shows the vertical electron density profiles of IRI- 2016 (blue) and the CIT (red) at the center of the Korean peninsula (37°N, 127°E). The CIT electron density profile is significantly reduced compared with that of IRI-2016, but the shape is quite similar each other. Since the EOFs can reproduce the IRI profiles within at least 93 %, as mentioned in previous section, the shape of the CIT profile is expected to resemble the IRI profile to that degree. Using the EOFs may smear out some features of true electron density profile and thus make it converge to the shape of IRI profiles. Therefore, the ionospheric irregularity or abnormal ionospheric vertical structure may not be reconstructed by the CIT algorithm, especially during geomagnetic storms. Despite the weak point of the EOFs, efficient computation still warrants their use in CIT reconstructions. Our CIT computation takes only about 2-3 min in a desktop computer environment (Intel Core i7 CPU, 16 GB RAM, not using GPU). Thus, it allows near real time CIT analysis using the 10 min interval GPS dataset.
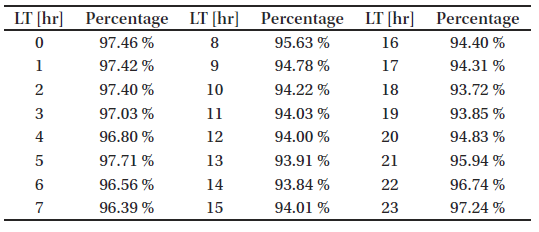
In order to validate the CIT results, we have performed two statistical analyses. One is a comparison with ionosonde measurements and the other is a comparison of the variation of VTEC over the local time and season with GPS observations. Each statistical validation was analyzed for two geomagnetic conditions with Kp index, greater and less than 4, during the first half of 2015. In this period, the solar flux index, F10.7, shows the minimum value of 94.8 and the mean value of 128.5.
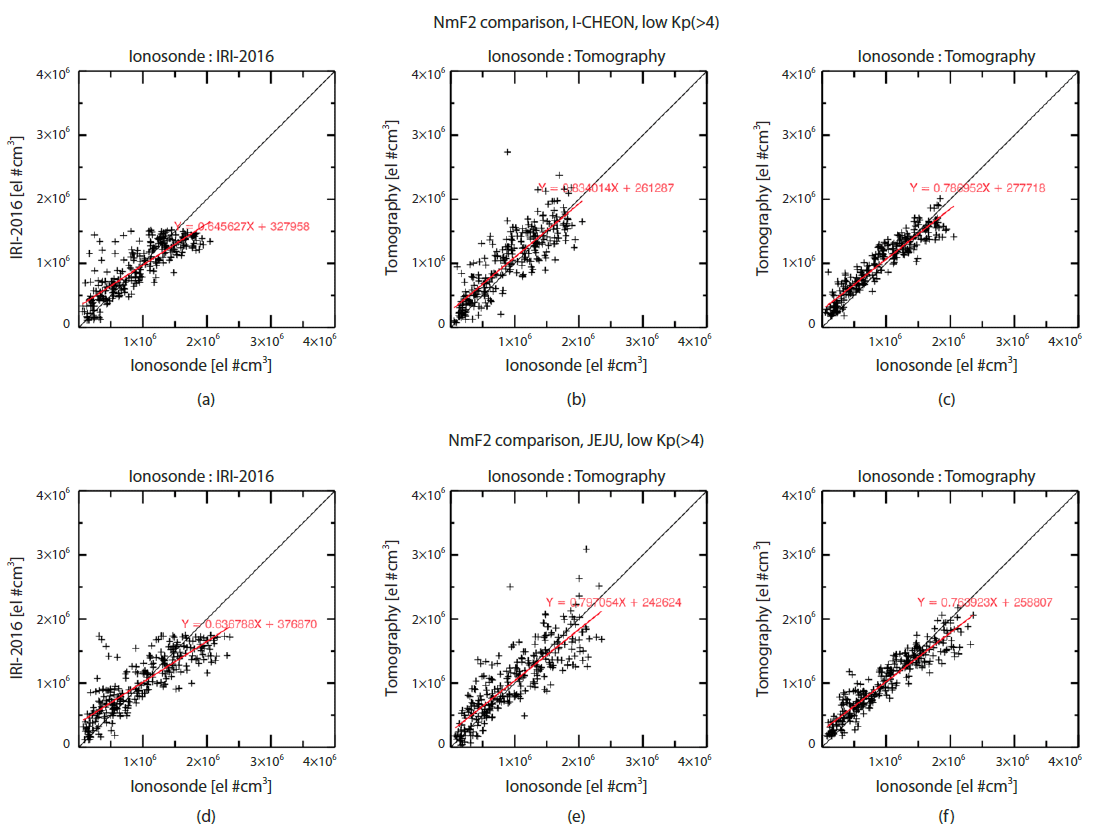
First, we utilized NmF2 data (maximum electron density) measured by ionosondes in Icheon and Jeju, South Korea. As mentioned above, the CIT applied EOFs result in the reconstructed profile shape similar to the IRI profiles, thus, the height of maximum electron density may not agree very well with the measured hmF2s (peak height of F2) by ionosondes. Future version of CIT will utilize more realistic EOFs that can represent electron profiles measured with various methods. We extracted hourly NmF2 data after filtering out low confidence level data, resulting in total 3,468 and 3,298 NmF2s from Icheon and Jeju ionosondes, respectively. We carried out the CIT using the 10 min GPS STEC dataset every hour for this period.
Fig. 6 shows statistical comparisons of the NmF2 values measured by ionosonde with those of IRI-2016 in panels (a) and (d), with those of the CIT that used revised STEC (with the PTEC removed) in panels (b) and (e), and with those of the smoothed CIT in panels (c) and (f). The data in Fig. 6 are all for low geomagnetic activity with the Kp index lower than 4. Upper and low panels are for Icheon and Jeju NmF2s, respectively. Black lines indicate one-to-one match between two NmF2 sources, and red lines are linear fits of scatter plots. The fitting slopes of the CIT are improved from 0.80 to 0.83 in Icheon and from 0.78 to 0.80 in Jeju, suggesting better agreement with ionosonde NmF2s. Note that the IRI-2016 model shows an upper limit of 1.5×106 cm-3 in Icheon and about 1.8×106 cm-3 in Jeju ionosonde stations, respectively. Similar upper limit can be also found in previous studies (Sojka et al. 2007; Yu et al. 2013; Ratovsky et al. 2015; Ratovsky et al. 2017). The upper limit is obviously the limitation of the empirical model and is not realistic. However, the unrealistic upper limits are not shown in the CIT results.
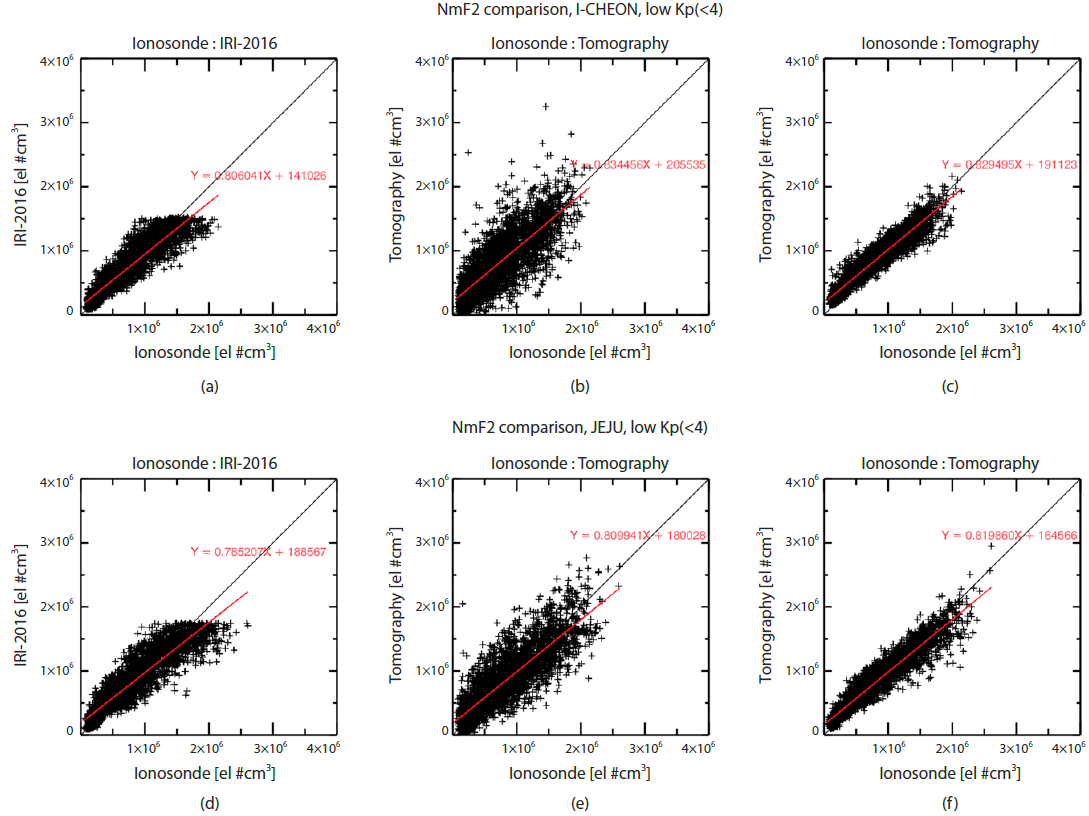
The CIT NmF2s computed by using original STEC data do not have significant offsets compared with NmF2 values of ionosondes. The offset values are reduced for the CIT with the removal of the PTEC in Figs. 6(b) and 6(e), as discussed in the previous section. Probably the remaining offset values are due to the inherent limitation of CIT that may be interfered by electron contents from E or F1-region below the F2 peak. The linear fits in Figs. 6(b) and 6(e) are close to the one-to-one line especially at larger than about 1.5×106 cm-3. Therefore, the CIT results with the removal of PTEC reasonably reconstruct the measured NmF2 for both stations.
Before performing the horizontal smoothing at each altitudinal plane, only the specific voxels that contain the GPS rays could be reconstructed by the MART algorithm. Horizontal smoothing allows more voxels to be affected by the given set of GPS rays. Even though the slopes of linear fits are almost unchanged, the final results of the CIT that adopted the horizontal smoothing show significantly smaller scatter around the linear fitted line in Figs. 6(c) and 6(f). Thus, the horizontal smoothing seems to improve the result of the CIT reconstruction.
Fig. 7 shows scatter plots similar to Fig. 6 but for during high geomagnetic activity. Red lines in Figs. 7(a) and 7(d) deviate more from black lines than those of during low geomagnetic activity. The upper limits of NmF2 are still apparent in the IRI-2016 NmF2s, same as in Fig. 6. The CIT results agree better with the ionosonde NmF2 than the IRI-2016 model, especially when the PTEC contributions were removed from the original GPS STEC values and the horizontal smoothing was performed for the reconstruction processes.
As a verification of the CIT reconstruction, we calculated relative VTEC differences (RVDs) at the center of Korean peninsula (37°N, 127°E) for IRI-2016 and the CIT results:
where VTECrev_GPS is the revised GPS VTEC after the removal of plasmaspheric VTEC. The VTEC values of IRI-2016 are also used for VTEC comparison. Fig. 8 shows the local time variations of RVD of IRI-2016 (left) and the CIT results (right) with respect to the revised GPS VTEC for low and high geomagnetic conditions during the first half of 2015. In spring and winter, under low geomagnetic condition, IRI-2016 overestimates the electron density during daytime while underestimates during night time. Especially, the RVD is large in winter, reaching almost ±60 %. Meanwhile, IRI-2016 yields the lower electron density than GPS observations in summer with relatively smaller offsets of about -20 %. It was found that the RVD increases with high geomagnetic activity. In particular, there was the greatest geomagnetic storm event of solar cycle 24 in spring, 2015. Therefore, the RVD differences in spring between high and low geomagnetic activities are significant. On the other hand, RVDs of the CIT results are significantly reduced compared with IRI-2016. RVDs are very close to zero in spring and summer during low geomagnetic activity. Despite the vast differences of initial guess of the IRI model in winter, most of the CIT results are within about ±20 % from the measured GPS VTEC values. For high geomagnetic activity, the CIT results still remain within ±20 % from the measured values except a few cases in spring when the extreme geomagnetic storm occurred.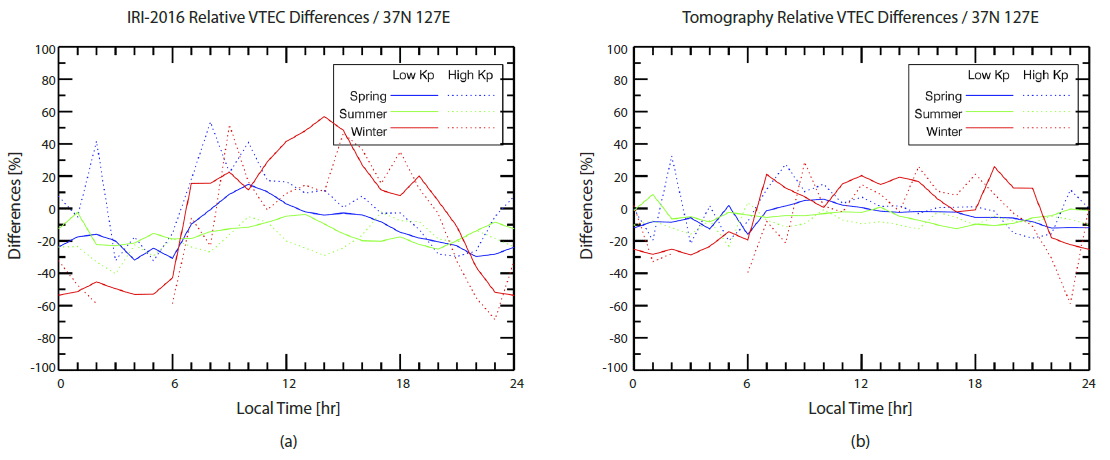
5. SUMMARY
We have developed a CIT code and applied the code to the ground based GPS dataset obtained with 10 min interval in South Korea. The latest version of IRI, IRI-2016, was used for the initial guess of the CIT. The actual length of ray paths through each voxel was calculated from ray tracing of GPS signal. We applied MART to solve the inverse of matrix equations. To complement the CIT for the lack of GPS signal paths, we have used EOFs derived from the IRI-2016 data set. The EOFs reduce the number of unknowns in the vertical direction of the matrix equations and thus regularize the solution search and reduce computation time as well. Even with the application of EOFs, some vertical direction profiles could not be controlled by GPS signal paths, causing discontinuous features, which were alleviated by horizontal smoothing. The CIT process takes only a few minutes with more than 9,000 STEC data in 10 min interval, which allows to reconstruct 3D features of the ionosphere over South Korea in near real time.
We compared the CIT results with ionosonde and GPS TEC data to validate the CIT code. The IRI-2016 model shows significant differences from ionosonde in NmF2 values. Especially, the IRI-2016 showed non-realistic upper limits of NmF2s over South Korea, while the CIT results showed better agreement with ionosonde NmF2s, compared to the IRI-2016 case. The CIT results were also verified by comparing the CIT computed VTEC with GPS VTEC data. After removing the PTEC contribution from the GPS VTEC, the differences between the CIT and GPS VTEC are within ±20 % for both low and high geomagnetic activity cases. In particular, the differences in spring and summer are quite close to zero. In conclusion, our CIT code can be utilized to monitor the 3D structure of the ionosphere over South Korea in near real time with currently available GPS TEC data.