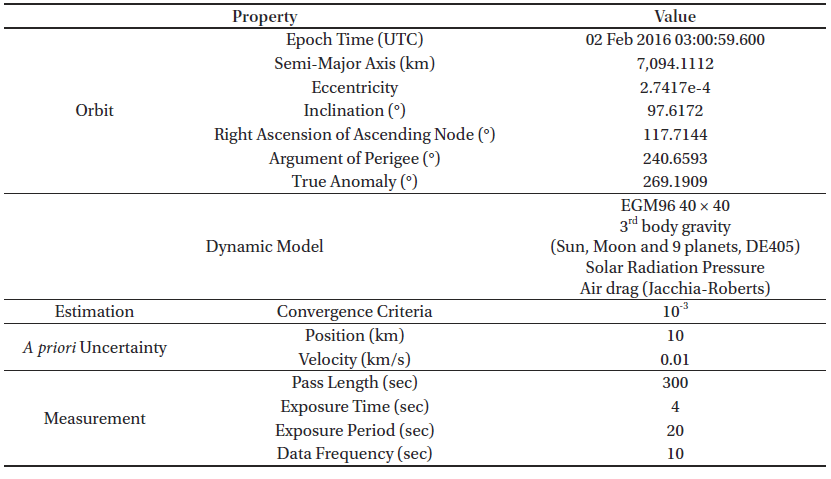
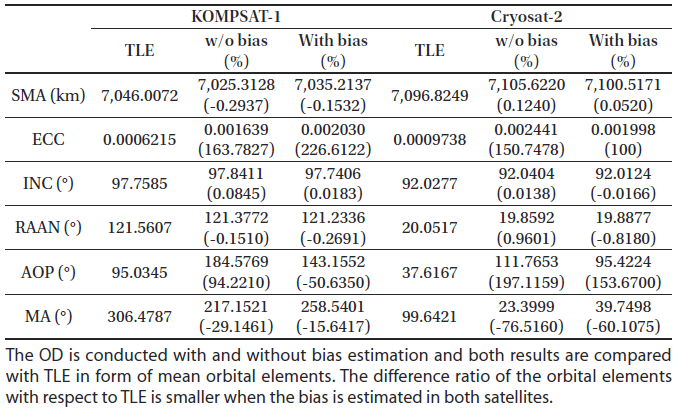
1. INTRODUCTION
Optical observation has been used to detect space objects and a considerable number of optical observation systems are available such as the ground-based electro-optical deep space surveillance (GEODSS; Henize et al. 1993), Lincoln near-Earth asteroid program (LINEAR; Stokes et al. 2000), and international scientific optical network (ISON; Molotov et al. 2008). The optical observation system is appropriate for the surveillance of space objects because it is not limited by the range to the object, unlike active tracking systems such as radar and laser. For this reason, a lot of research on orbit determination (OD) using optical measurements has been conducted. Sabol et al. (2007) developed a simplified covariance model to predict the orbital error uncertainty and demonstrated that high-accuracy orbit updates from angle-only data are available only if the eccentricity has a low uncertainty. Vallado & Agapov (2010) introduced OD results of geosynchronous (GEO) satellites using highquality optical data from ISON; an uncertainty of ~5 km was obtained using the least squares method. Tombasco (2011) addressed GEO orbit estimation using ground-based and space-based angle-only measurements and enhanced the accuracy based on GEO elements.
The optical wide-field patrol network (OWL-Net) is an optical surveillance system of space objects developed at the Korea Astronomy and Space Science Institute (KASI). The main goals of the system are the tracking and monitoring of domestic satellites to protect space assets. There are five observatories around the world, in Korea, Mongolia, Morocco, Israel, and the USA. The OWL-Net provides topocentric right ascension and declination measurement data converted from the image pixel coordinates (Park et al. 2013).
The orbital states of low earth orbit (LEO) satellites were evaluated in previous studies based on OWL-Net data. Jo et al. (2015) utilized commercial OD software to achieve preliminary OD results and showed that the requirements of OD can be achieved. In another study, Park et al. (2015) utilized the same software and analyzed the OD accuracy according to the number of estimation points.
In this study, OD software for the optical surveillance of space objects was developed and the orbital states of two LEO satellites, KOMPSAT-1 and Cryosat-2, were determined using the software and OWL-Net data. In addition, the precision and accuracy of OWL-Net data were analyzed based on the simulation of potential error sources of OWLNet measurements such as noise, bias, and clock errors. The software is available to operate independent optical surveillance systems of space objects.
The batch least squares algorithm is introduced and verified in Section 2. The error sources of the OWL-Net are analyzed in Section 3. The estimation results using actual data are addressed and compared with known orbital information in Section 4 and Section 5 summarizes this paper.
2. BATCH LEAST SQUARES FILTER
The batch least squares algorithm is a post-processing estimation algorithm known as differential correction. It processes all data in a lump to determine the epoch states. Although this procedure is not appropriate for real-time systems, it is generally used because of some advantages. The batch estimation is simple and more accurate and robust compared with sequential estimation algorithms, such as the Kalman filter (Crassidis & Junkins 2011).
This section mathematically describes the algorithm including definitions of cost function, covariance matrix, and convergence criteria.
The batch least squares algorithm estimates epoch states using a system model (F):
In case of OD, Y is the measurement data set, ϵ is the measurement noise vector, and X is a solve-for-vector, which is required such as the position and velocity vector (Schutz et al. 2004). The system model can be separated into dynamic and measurement models.The estimation can be referred to as an optimization, which minimizes the cost function (Q), weighted sum of the squares of the measurement residual, and the difference from a priori states:
where and are the a priori covariance matrix and state vector, respectively, and W is the weight matrix. The a priori covariance matrix and weight matrix reflect the a priori uncertainty and measurement white noise, respectively: where is the standard deviation of the jth element of the solve-for-vector, n is the dimension of the solve-for vector, and m is the number of measurement data.If the a priori states are close enough to the true states, the system model and cost function can be linearized using the Taylor expansion. Hence, a normal equation is derived to evaluate the variate of the ith iteration (ΔXi) and the solve-for-vector is then updated (Long et al. 1989):
where H is the Jacobian matrix, a partial derivative of the system model. It can be divided into state transition matrix (Φ) and sensitivity matrix (A) using the chain rule.
When the solve-for-vectors are the Cartesian position and velocity vector , and the measurement data consist of topocentric right ascension (α) and declination (δ), the sensitivity matrix is simply formulated:
where ρ is the relative position vector of the object with respect to the observatory i.e., . If the measurement bias (β) is also estimated, following terms are added to the Jacobian matrix:
where k is the scaling parameter, which is set to one by default.
The whole process, which includes the prediction and update, is iterated until convergence is achieved. The con-vergence criterion is the cost reduction ratio (γ):
The estimation sequence is finished if the ratio becomes less than a small tolerance (ε) set as 10-3 by default, and it also terminated if the ratio is negative, which means increasing cost and maximum number of iterations are reached.
The covariance matrix (P), which contains the statistical information of the estimation, is evaluated after convergence. The covariance matrix is evaluated as follows:
In this study, the general mission analysis tool (GMAT) is used as the dynamic model (Hughes et al. 2014) and the state transition matrix is numerically evaluated.
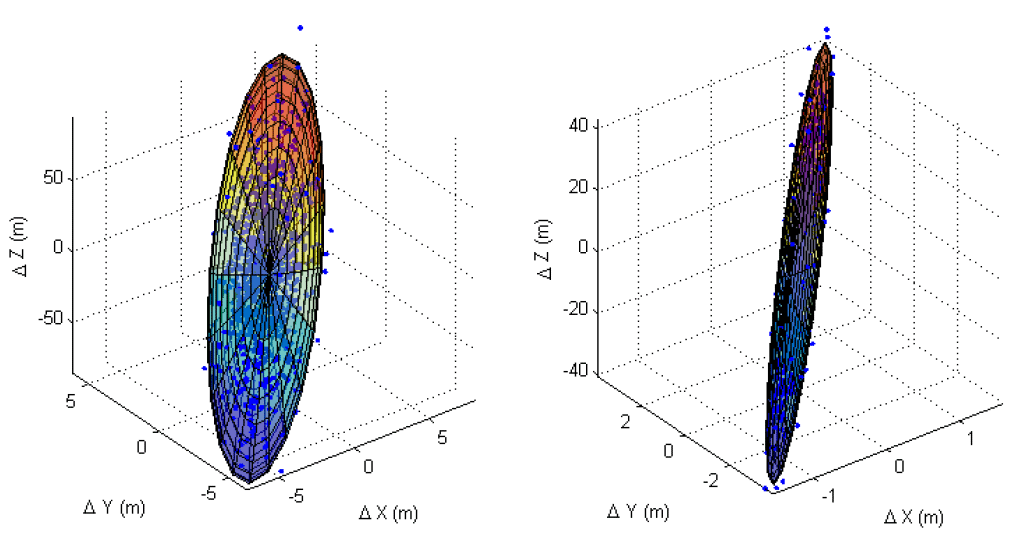
The covariance matrix estimated from the estimation algorithm has a statistical meaning and addresses the precision of the estimation. To confirm the validity of the estimated covariance matrix, Monte Carlo simulations were conducted and the results were compared. If the estimated covariance is equal to the results, the estimation is valid.
Monte Carlo simulation was conducted for two different cases: states estimation with unbiased measurement data (Case 1) and states and bias estimation with biased measurement data (Case 2). Each case is simulated 1,000 times using the LEO. Table 1 lists the detailed configuration of the simulation. Instead of GMAT, two-body dynamics were assumed for simplification purposes based on the statistical independence of the system model. The pseudo-measurement properties of the OWL-Net measurement are as follows: the pass length is an observable period; exposure time is the time when taking a picture; exposure period is the timespan between two pictures; the data frequency is the number of extracted data points per second.
|
The precision of the estimation can be evaluated by the integration of a multivariable probability function. Especially in the case of multivariable space, several methods can be used to interpret the uncertainty of the variables such as the hyper-rectangle and hyper-ellipsoid methods (Long et al. 1989). The probability that the three-dimensional position vector is within the 3σ range, for instance, is ~97 % and ~99 % based on the hyper-ellipsoid and hyper-rectangle methods, respectively. In this study, the hyper-ellipsoid method was used because the hyper-rectangle probability is a simple extension of the single Gaussian probability function.
In both cases, the algorithm was verified based on the statistical significance (97 %) of the results of the covariance ellipsoid. Fig. 1 shows the comparison between the results of the Monte Carlo simulation and the estimated covariance ellipsoid for both cases. Note that they are used only for algorithm verification and not for performance validation.
3. ERROR ANALYSIS
As opposed to the simulated observation, which only has Gaussian white noise, the real observation has more error sources such as bias and clock errors. In this section, the effects of noise, bias, and clock errors are determined using simulations of pseudo-measurement data. The analyzed relationship of each error source with the OD result can be used to interpret and predict the actual OD result. Table 2 lists common environments of all types of error analyses.
Noise is a random error generated by thermal radiation. It is equal to the precision of the observation and cannot be exactly estimated and corrected. To check the effect of noise on the accuracy of the estimation, the OD simulations were conducted 100 times using pseudo-measurements and varying noise levels from 1 to 150 arcsec without bias. Note that the range of noise level is set as a known property of the OWL-Net measurement.
As a result, the residual exhibits the same distribution as the noise but without any trend (Fig. 2), which means that the resultant residual distribution can be conversely used to analyze the observation quality. In addition, the developed batch least squares filter reduces the a priori state error irrespective of the measurement noise.
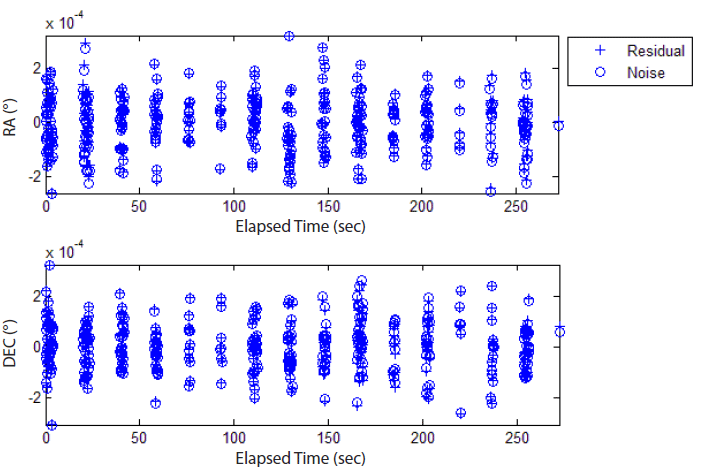
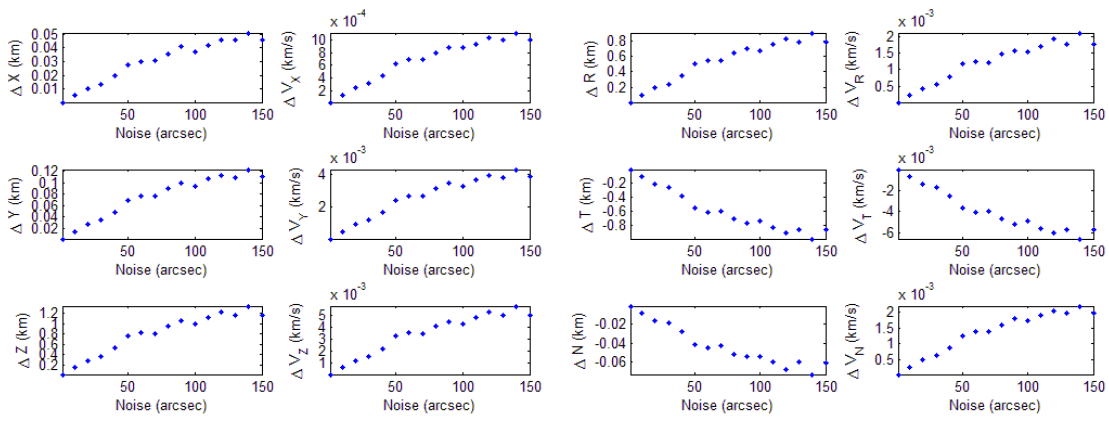
Fig. 3 shows the root-mean-square (RMS) error of each state in earth centered inertial (ECI) and radial-tangential-normal (RTN) coordinates. It is directly proportional to the noise level, that is, the observation precision, and much smaller than the a priori error. The magnitude of the position error depends on the axis, especially that of the z-axis and radial error are larger than that of other axes. This might be due to the characteristics of the optical observation, which cannot include the line of sight direction information.
Bias can be caused by various factors such as coordinate transformation, catalog matching errors, and clock errors (Son et al. 2015). Although it might not be a constant due to the nonlinearity of the system, it is considered as a constant for a short arc for simplicity in this paper. To examine how the bias affects the OD, the OD simulations were conducted 500 times using pseudo-measurements. The pseudo-measurements are generated with a random bias of 3° (1σ), which is not estimated, and a noise level of 40 arcsec. Note that the magnitude of the bias is set large enough to include many bias causes.
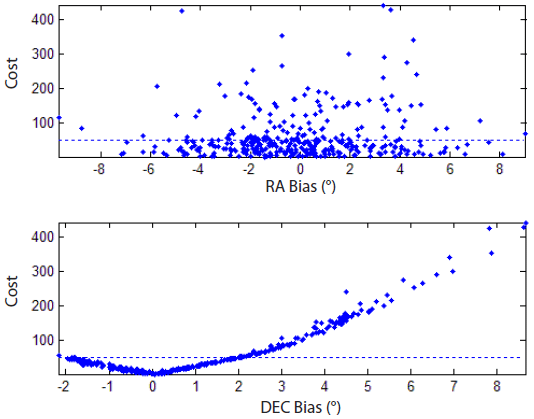
Approximately 70 % of the estimations converged; however, only 35 % of them converged with a proper answer and 30 % of the estimations even terminated in divergence. The results do not depend on the right ascension (RA) bias but they strongly depend on the declination (DEC) bias (Fig. 4). The estimation converges only if the DEC bias is larger than approximately -2°, whereas there is no dependence on the RA bias. The estimation accuracy of the normal cases is on the order of kilometers and that of wrong cases is on the order of several hundreds of kilometers. A separation criterion between normal and wrong cases is the cost (Eq. (2)) of 50, where the cost of unity represents that the a priori error is removed and the residual is normalized. Fig. 5 shows that the RA bias is randomly distributed, regardless of the criterion, while the DEC bias is notably separated due to the criterion.
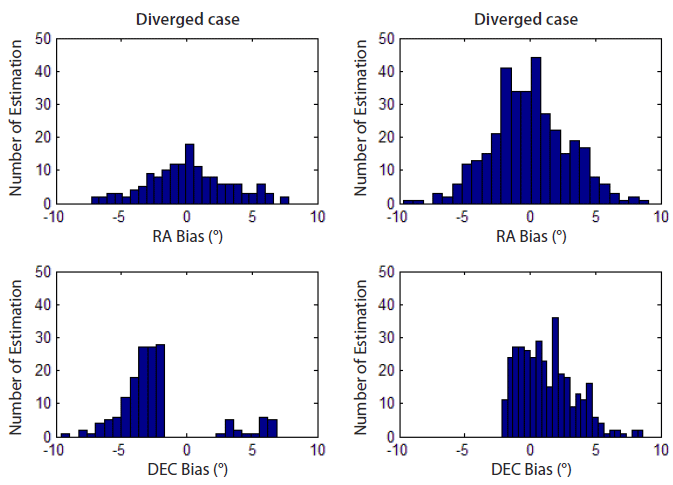
This result probably depends on the orbit. Because the simulated orbit is almost polar (inclination of 97°), the declination changes more than the right ascension and the DEC bias is more influential than the RA bias. The relationship between the orbital characteristics and the effect of bias will be analyzed in the future.
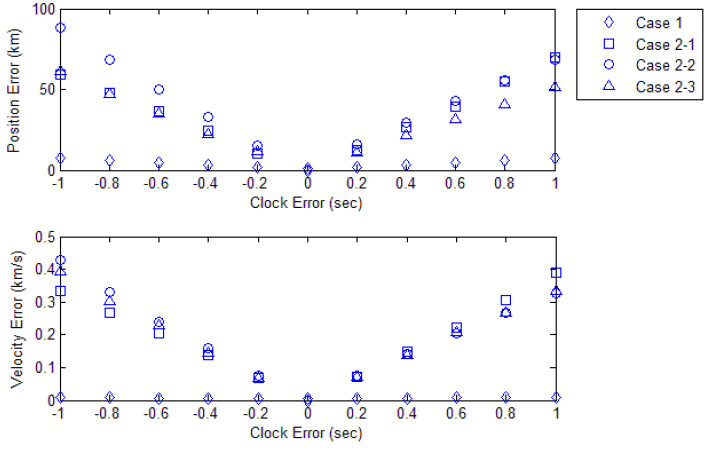
The OWL observatory synchronizes time using a network time protocol (NTP) server, which has a precision on the order of 0.001 sec (Son et al. 2015). The data reduction algorithm includes a step to combine the extracted data points and time log (Park et al. 2013) based on which two types of clock errors are simulated. The first error is the time-synchronization offset (Case 1), where the whole time log is shifted. The other error is the time-tagging error (Case 2), where parts of the time logs are shifted. In case of the time-tagging error, the portions of the shifted observation are 25 % (Case 2-1), 50 % (Case 2-2), and 75 % (Case 2-3). All cases are simulated 100 times with a noise level of 15 arcsec corresponding to the OWL-Net without bias.
Fig. 6 describes the effects of all types of clock errors onto the position and velocity. In case of the time-synchronization offset, the position error ranges from 1.5 to 7.6 km because the offset increases from 0.2 to 1 sec. The result corresponds to the orbital motion of LEO (~7 km/s). In contrast to the overall time offset, the time-tagging error is an error source that leads to irregular observation data. In Case 2-1, the cost is minimized when the estimated state corresponds to the normal measurement because only 25 % of the measurement data have clock errors. On the other hand, 75 % of the measurement data have clock errors in Case 2-3 and the estimation thus corresponds to the error measurement. The estimation error is largest because the normal and abnormal measurements occupy the same portion in Case 2-2. In conclusion, the biggest state error is ~90 km in Case 2-2; Cases 2-1 and 2-3 have a similar level of state error.
4. OWL-NET APPLICATION
The OWL-Net observation data (topocentric right ascension, α, and declination, δ) of two LEO satellites, KOMPSAT-1 and Cryosat-2, are available. KOMPSAT-1 is a Korean Earth observation satellite at an altitude of 685 km, which was launched in 1999 and completed its mission in 2008 (Kim et al. 2015). Cryosat-2, is another Earth observation satellite mission managed by the European Space Agency (ESA). It was launched in 2010 and measures the thickness of sea ice using radar altimetry at an altitude of 725 km (Kurtz et al. 2014). The data were applied to the estimation algorithm, which was verified to provide reliable estimation results. Furthermore, the characteristics of OWL-Net observation data were determined based on the error analysis explained in Section 3.
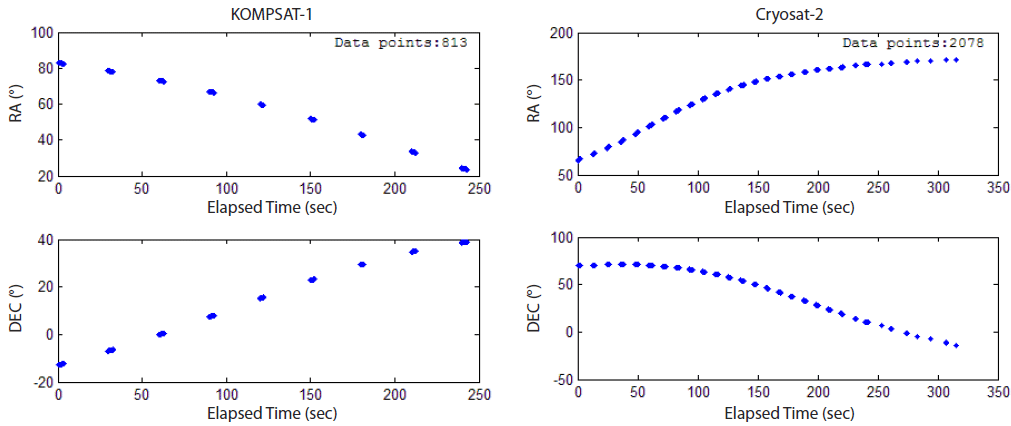
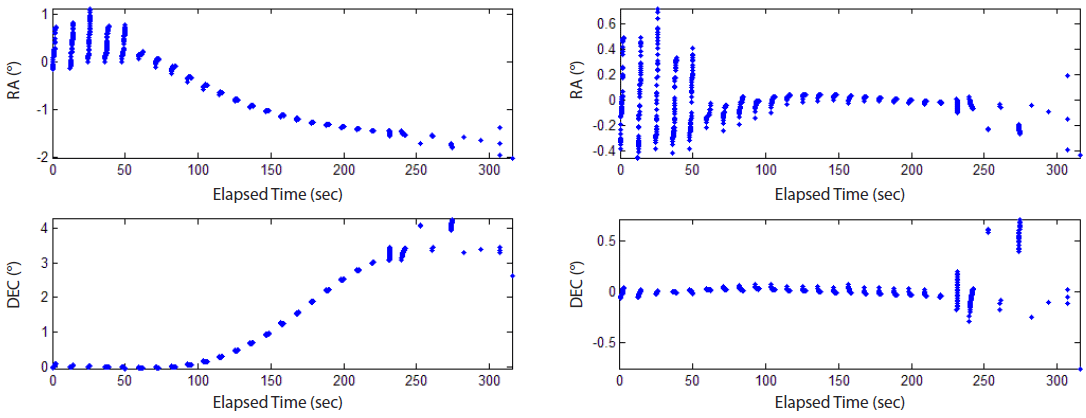
The OWL-Net observation data were provided in form of report files, which include the name of the target satellite, location of the observatory, exposure time, charged-coupled device (CCD) temperature, and time-tagged data points. Each file reflects a tracking pass of the satellite and consists of pictures from which the data points were extracted. Fig. 7 shows the data points extracted from a report file of KOMPSAT-1 and Cryosat-2. The arc of 4 min measured on November 5, 2014, and the arc of 5 min measured on May 25, 2015, were used for KOMPSAT-1 and Cryosat-2, respectively. Note that the properties of the arc, such as length, extraction period, and number of data points, are different in the two cases.
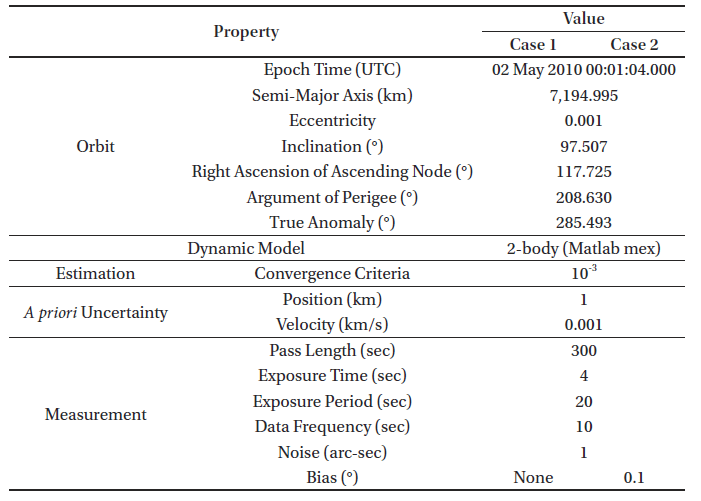
The orbit of each satellite was determined using OWL-Net observations and the developed algorithm (Section 2). The OD is conducted with and without bias estimation. The results of the Gauss method, which is one of the initial OD techniques, were used as a priori states. Other configuration details are listed in Table 3.
|
In case of KOMPSAT-1, the residual uniformly decreased from about 0.1° to 14 arcsec throughout the whole observation for both RA and DEC (Fig. 8). The estimated biases are 0.2738° and -0.0148° for RA and DEC, respectively.
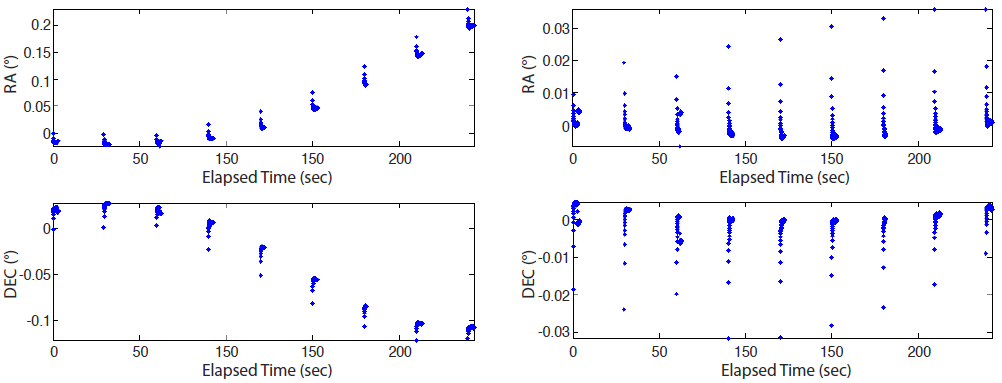
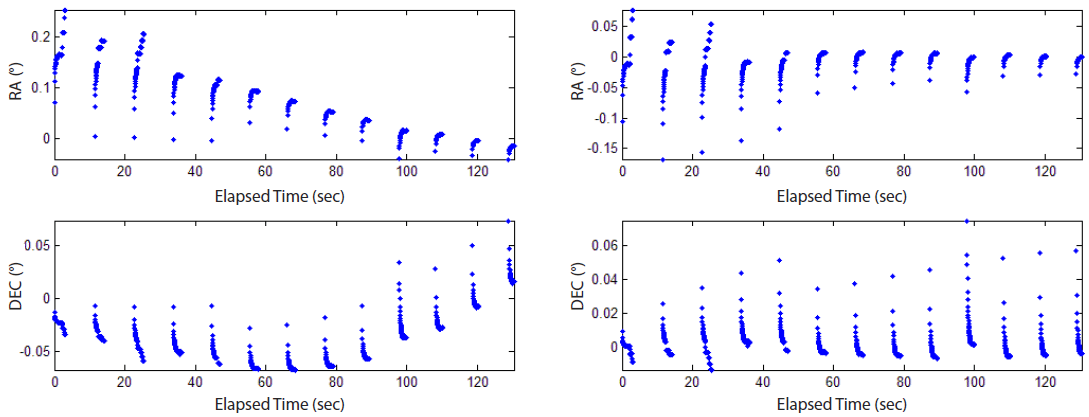
The residuals of Cryosat-2 also reduced from several degrees to ~0.1° after OD processing. The pattern, however, is quite distinct from that of KOMPSAT-1; the residual is not uniform but exceptionally large in the beginning and end of the observation (Fig. 9). For this reason, only the middle part of Cryosat-2 data was used for OD, that is, data editing. To exclude abnormal measurement data from the OD process, data points extracted from specific pictures were removed, while the editing usually eliminates part of the measurement of the threshold such as 3σ (Long et al. 1989). After data editing, the RA and DEC residuals are 74 and 28 arcsec, respectively (Fig. 10). The estimated RA bias is -0.0569° and the DEC bias is 0.0590°.
The results were compared with the two-line elements (TLE) of the corresponding satellite to determine the ac-curacy of the estimation. The direct comparison of the Cartesian states, however, is improper because the estimated ephemeris has an accumulated error due to the epoch state and system errors. For this reason, the estimation result is compared with TLE in form of mean orbital elements, which do not change much due to orbital motion (Table 4). The estimation of the bias shows that the difference of the orbital elements with respect to TLE is smaller in both satellites. The differences of the semi-major axis (SMA), inclination, and right ascension of the ascending node (RAAN) are < 1 %. Because both orbits are almost circular, the arguments of the perigee and mean anomaly do not match well but their sums (argument of latitude) do. The eccentricity, however, is estimated to be several times the TLE, which might be due to the velocity error.
Furthermore, the result of the Cryosat-2 estimate was compared with the reference trajectory, which was published in consolidated prediction format (CPF) based on the international laser ranging system (ILRS) (Pearlman et al. 2002). The predicted trajectory is generated by prediction centers and regularly checked by several analytic centers, such as the Natural Environment Research Council (NERC); the accuracy is approximately several hundreds of meters (NERC Space Geodesy Facility 2017). It presents the three-dimensional position in the true-body-fixed of date system of the international terrestrial reference frame (ITRF). In this study, CPF data provided by ESA were used to analyze, where the epoch time of the trajectory is at 0:00 am on May 25, 2015, which is consistent with the observation date; the time interval of the position is 3 min. Fig. 11 shows the position difference in ITRF and RTN coordinates; each reference point is interpolated by the tenth order polynomial. The position difference at the epoch is ~0.8 km and most of the difference corresponds to the radial component and to the result of the simulation in Subsection 3.1. The result is similar to the results of previous studies, which reported that the RMS difference between TLE and the estimated orbit is < 10 km in case of Cryosat-2 (Park et al. 2015).
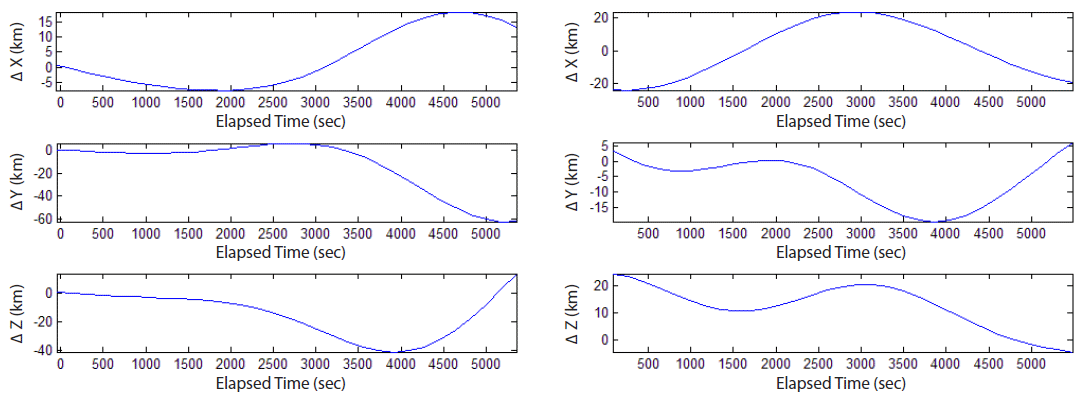
Considering the field of view of the OWL-Net, which is 1.75° (Park et al. 2012), the position error of the LEO satellites should be lower than 20 km at the next arc for tracking. Fig. 12 shows the position difference of the estimated orbit and TLE with respect to the reference trajectory in ITRF. Both are propagated for 90 min, a period of the LEO satellite; the maximum position difference of the estimation is ~70 km, while the TLE difference is ~30 km. This might be due to the velocity difference, which is also related to the eccentricity error. The estimation accuracy can be improved by resolving unknown error sources of the OWL-Net (Jo et al. 2015).
Based on the error analysis that shows that the precision of the measurement data is the same as that of the residual, the precision of the OWL-Net observation data is tens of arcsec. Based on the bias estimation, the accuracy of the observation data is also determined to be of sub-degree level.
5. SUMMARY AND CONCLUSIONS
Optical observation is suitable for the surveillance of space objects. The OWL-Net is a Korean optical surveillance system that tracks and monitors domestic satellites. In this study, the orbital states of two LEO satellites were determined using OWL-Net data and a batch least squares filter, which was developed and statistically verified. In addition, the precision and accuracy of OWL-Net data were analyzed based on the results of software simulations for error analysis.
The batch least squares filter processes all data to determine the epoch states; it is more robust to temporal measurement errors. The objective function is defined as the sum of the weighted residual and difference of the a priori states. The system model is composed of dynamic and measurement models. In this study, GMAT was utilized as the dynamic model and geometric RA/DEC was used as the measurement model. The system model was linearized to estimate the most probable epoch states; it turns into the states transition matrix and sensitivity matrix, where each matrix is numerically evaluated and analytically derived.
For statistical verification, Monte Carlo simulation was performed under two different conditions (unbiased meas-urement data without bias estimation; biased measurement data with bias estimation) and the results were compared with the covariance matrix. The results correspond to the multivariate analysis of the covariance in both cases, where 97 % of the estimation results plot inside the 3σ covariance ellipsoid.
Potential error sources of OWL-Net, noise, bias, and clock errors were analyzed using software simulations. The estimation accuracy depends linearly on the noise level and the declination bias has a significant influence on the estimation in a polar orbit. The estimation converges only with a DEC bias larger than approximately -2° and the estimation error increases to > 100 km when the DEC bias is larger than 2°. This is due to the orbital characteristics, although it is not the general feature. Two types of clock errors were analyzed, time synchronization offset and time-tagging error. The position error is ~7.6 km at a time-synchronization offset of 1 sec, which corresponds to an orbital velocity of ~8 km/s of LEO. The time-tagging error, however, increases the position error up to 90 km because it leads to irregular observation data.
The OWL-Net measurement data of KOMPSAT-1 and Cryosat-2 were provided by KASI and applied to the batch least squares algorithm. The Cartesian states were estimated by default and the measurement bias was optionally estimated. The estimated orbital states of both satellites are similar to those of TLE; however, the eccentricity error is significantly large. In case of Cryosat-2, the estimated trajectory was compared to the CPF trajectory in ITRF. Its difference is 0.8 km at the epoch time, which is similar to that of TLE and is in agreement with previous results (Park et al. 2015). However, the difference is ~70 km after 90 min, while the corresponding value of TLE is ~30 km. The precision of the OWL-Net data is tens of arcsec and the accuracy is of sub-degree level.
This study has nobility to demonstrate the operating capability of independent optical surveillance system of space objects. Unlike previous studies, which employed commercial software to examine OWL-Net measurement data, this study utilizes newly developed OD software. The results are similar to those of TLE. Because the software was statistically verified and examined under various conditions, the results are reliable and indicate the possibilities of independent space surveillance operations. The position error, however, increased when orbit propagation was performed, which might be due to the velocity error and can be improved through the use of parameter tuning and nonlinear estimation techniques. Furthermore, the precision and accuracy of OWL-Net measurement data was determined by interpreting the OD results. The performance of the OWL-Net can be improved by stabilizing the system to resolve unknown error sources; other reliable optical measurements can be used to check the performance of the OD software and analyze OWL-Net measurement data in the future.