1. INTRODUCTION
The auroral oval, a ring-shaped region encircling Earth’s magnetic poles, signifies the upper-atmospheric footprint of charged particles from the solar wind and the magnetosphere that are guided along Earth’s magnetic field lines. The oval is typically located between about 65° and 75° magnetic latitude under quiet geomagnetic conditions. There, these energetic particles collide with oxygen and nitrogen, emitting visible lights as aurora (Feldstein & Starkov 1967; Holzworth & Meng 1975; Evans 1986; Kivelson & Russell 1995; Ebihara & Ejiri 2000; Grocott et al. 2009). The auroral oval is maintained by magnetospheric convection driven by dayside reconnection and nightside substorms. The nightside portion of the oval is typically broader than the dayside, reflecting enhanced particle injection from the plasma sheet and expansion of the westward electrojet during substorm activity (Lockwood & Cowley 1993). Field-aligned currents (FACs) flow along closed, high-latitude magnetic field lines that map to the plasma sheet in the magnetotail and close through the auroral electrojet region in the ionosphere which forms the oval encircling the geomagnetic poles (Iijima & Potemra 1976).
The offset between the geographic and magnetic poles, along with the tilt of Earth’s magnetic dipole, causes the auroral oval to appear asymmetrical in geographic coordinates but more circular in geomagnetic coordinates. However, asymmetry between day and night as well as dawn and dusk does exist in the magnetic coordinates.
The latitudinal span of the auroral zone depends on the radial distance in the plasma sheet, local time sector, and geomagnetic activity and solar wind and interplanetary magnetic field (IMF) conditions. In particular, on day side, particle precipitation comes from cusp and boundary layer sources, and the oval is typically narrower in latitude here. On nightside, more intense and broader auroral activity due to plasma sheet injections and substorm equatorward expansion (Sergeev et al. 2012). At dawn/dusk sectors, asymmetries arise from the east–west electrojets and IMF By effects.
The precise location of the auroral oval can be determined using a combination of satellite-based imaging, ground-based optical observations, magnetometer arrays, in situ particle measurements, and other ionospheric measurements. Ultraviolet (UV) imagers onboard satellites such as POLAR, IMAGE, and DMSP provide global views of auroral emissions in the farultraviolet (FUV), enabling accurate mapping of the large-scale structure inside the oval (Frey et al. 2001; Zhang & Paxton 2008). Ground-based all-sky imaging (ASI) cameras offer high-resolution optical imagery of auroras in visible wavelengths (e.g., 557.7 and 630.0 nm), revealing fine-scale features and temporal evolution (Shiokawa et al. 1996; Donovan et al. 2006). Arrays of ground magnetometers, such as SuperMAG and IMAGE, track variations in horizontal magnetic fields to infer the strength and location of auroral electrojets, which align closely with the auroral oval (Gjerloev 2012). In situ particle detectors on satellites like DMSP and FAST measure precipitating energetic electrons and ions, directly identifying the boundaries of particle precipitation that define the auroral region (Newell et al. 1996). The THEMIS mission has significantly enhanced understanding of auroral dynamics by combining a constellation of satellites with ground-based ASIs and magnetometers, enabling direct observations of substorm onset and the temporal evolution of auroral structures (Angelopoulos 2008). The fluxgate magnetometer (FGM) onboard CHAMP provides extensive FAC density estimations which were used to develop a new auroral oval model, assuming the FAC enhancements occur within the oval (Xiong & Lühr 2014; Xiong et al. 2014). Additionally, high-latitude incoherent scatter radars (e.g., EISCAT, PFISR) detect ionospheric responses to auroral activity, such as enhanced electron densities and ion drifts (Nicolls & Heinselman 2007). These diverse measurements feed into empirical models, such as the OVATION Prime model, which statistically characterizes the location and intensity of auroras (Newell et al. 2014).
Global Navigation Satellite Systems (GNSS), such as GPS, GLONASS, and Galileo, have become powerful tools for auroral science, particularly in studying the ionospheric disturbances that accompany the auroral activity. When GNSS signals pass through the auroral ionosphere, they are affected by variations in electron density, especially during geomagnetic storms and substorms. Dual-frequency GNSS receivers are widely used to derive total electron content (TEC), which provides critical insights into electron density variations caused by particle precipitation, polar cap patches, subauroral ionospheric structures, and traveling ionospheric disturbances (Foster & Burke 2002; Foster et al. 2005; Zhang et al. 2013; Zou et al. 2014; Zhang et al. 2017a; Lyons et al. 2019; Zhang et al. 2019b; Nishimura et al. 2020; Zou et al. 2021; Zhang et al. 2022). Auroral processes also induce phase and amplitude scintillations of GNSS signals, making GNSS a powerful tool for detecting plasma irregularities and turbulence in the auroral ionosphere. The ionospheric irregularities can be monitored by using a GNSS index, ROTI (Rate of TEC Index change), as originally proposed by Pi et al. (1997) and now widely used for high, midlatitude, and equatorial science (Jakowski et al. 2012; Cherniak et al. 2014, 2018; Mrak et al. 2020; Sun et al. 2024). This index characterizes the intensity of the GNSS phase fluctuations caused by ionospheric irregularities. The present study, however, analyzed the mesoscale component of the TEC fluctuations, denoted as differential TEC (dTEC), to characterize the intensity of ionospheric irregularities inside the auroral over and polar cap region. The spatiotemporal scales of these irregularities are much larger than those associated with GNSS scintillations, ranging from sub-kilometers (small scales) to > 10 km (large scales). The dTEC method, which will be described in Section 2, has been widely utilized in the study of traveling ionospheric disturbances (TIDs; Saito et al. 1998) and ionospheric penetration electric field (Zhang et al. 2023). In the high-latitude region, dTEC could be related not only to TIDs, but also to ionization enhancement caused by sudden deposition of energetic particles, as well as to small intensity of plasma patches (Nishimura et al. 2020).
Global GNSS TEC data have been produced daily at Massachusetts Institute of Technology (MIT) Haystack Observatory since the start of widely scientific application of GPS data around 2000 and are archived in the Madrigal database (http://openmadrigal.org) for public use. Using these extensive GNSS data from 2010 to 2024, we explore the general climatology of mesoscale fluctuation levels of ionospheric electron density and establish their connection with the morphology and dynamics of the auroral oval.
2. DATA AND METHODS
MIT Haystack Observatory has developed the MAPGPS software suite to process GNSS observations, enabling the generation of global maps of TEC (Rideout & Coster 2006; Vierinen et al. 2016). The system currently utilizes data from over 6,000 global receivers contributed by community members, with a significant portion, exceeding 3,000, originating from the American sector. This extensive dataset comprises an astonishing 150 million line-of-sight (LOS) segments every single day. These LOS data enable the daily determination of TEC fluctuations, which are calculated as differential TEC (dTEC). This continuous spatial-temporal coverage provides the necessary information for the systematic statistics presented here.
Ionospheric perturbation in TEC, dTEC, is obtained by detrending the smooth background vertical TEC variations using LOS slant TEC data from each individual pair of receiver-GNSS satellite. This general approach was initially proposed by Saito et al. (1998) and is now widely adopted by the community to study TIDs (Ding et al. 2007; Zakharenkova et al. 2016; Zhang et al. 2017b; Chou et al. 2018; Mrak et al. 2018; Inchin et al. 2023).
In the present study, the background vertical TEC is determined by using a low-pass filter (Savitzky & Golay 1964) with a linear basis function within a 30-minute sliding window (Coster et al. 2017; Zhang et al. 2017b, 2019a). The filter algorithm uses a convolution process with least squares fitting of successive subsets of windows of 30 minutes involving time-adjacent TEC data points from the same GNSS satellite-receiver pair and a linear basis function set. The 30-minute window is appropriate in detecting medium scale irregularities most effectively at midlatitudes or for structures moving below 300–400 m/s; but for high latitudes with convective speeds above 1,000 m/s, the scale size of the irregularities can be up to 2,000 km. A 15° cut-off elevation for receiver-satellite ray paths was used to eliminate data close to the horizon. Data at the start and the end of each continuous segment from the same GNSS satellite-receiver pair were disregarded to avoid potential “edge” effects (Zhang et al. 2019a, 2021), which arise because of lack of data in the 30-min window centering around the data edge. The dTEC accuracy is based on the GNSS phase measurement error, which is often less than 0.03 TEC unit (TECu, 1 TECu = 1 × 1016 el/m2) (Coster et al. 2012), as all satellite and receiver bias terms cancel out in a differential sense. These dTEC values have been extensively used in studies related to TIDs such as those associated with solar eclipses, solar flares, solar terminator, geospace storms and substorms, volcanic eruptions, and lower atmospheric forcing (Zhang et al. 2017b; Lyons et al. 2019; Zhang et al. 2019a, b; Nishimura et al. 2020; England et al. 2021; Zhang et al. 2021, 2022; Chang et al. 2022; Lu et al. 2024; Tyska et al. 2024; Schmidt et al. 2025; Trop et al. 2025) and sudden global ionospheric disturbances associated with the penetration electric field (Zhang et al. 2023).
Fig. 1 provides some examples of TEC observations, the smooth background, as well as the fluctuation component (denoted as dTEC) along with GNSS satellite elevation and ionospheric pierce point information. The observations in (a) and (b) came from stations underneath the auroral region during the 7 September 2017 intense geomagnetic storm, where fluctuations up to ± 1.5 TECu can be found in (a) and ± 4 TECu in (b). (c) and (d) were at higher latitudes where the clear oscillations in (c) are potentially related to TIDs on 7 September 2017 and the large density spikes of ~30 TECu in (d) were likely plasma patches on 10 October 2024.
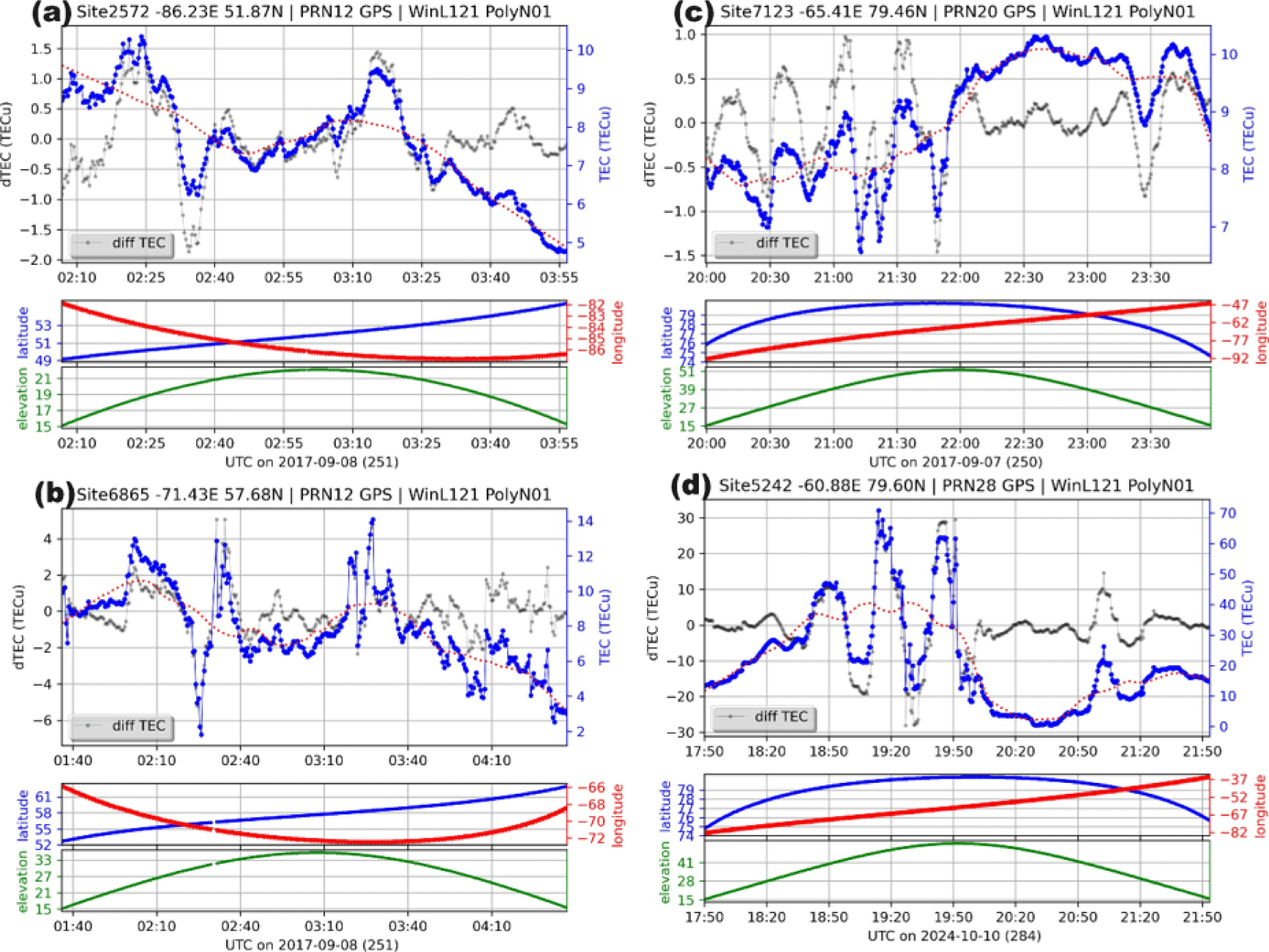
It is important to note that the GNSS observations collected using the MIT TEC processing system have varying temporal resolutions. While a significant portion of the data has a sampling rate of 1 min, 1-sec sampling rate is also widely available. Therefore, we resampled the data with a standard rate of 15 sec through either resampling or linear interpolation. After this procedure, the data is subjected to filtering and detrending steps to calculate dTEC, as mentioned earlier. The final dTEC are resampled data with the original temporal resolution.
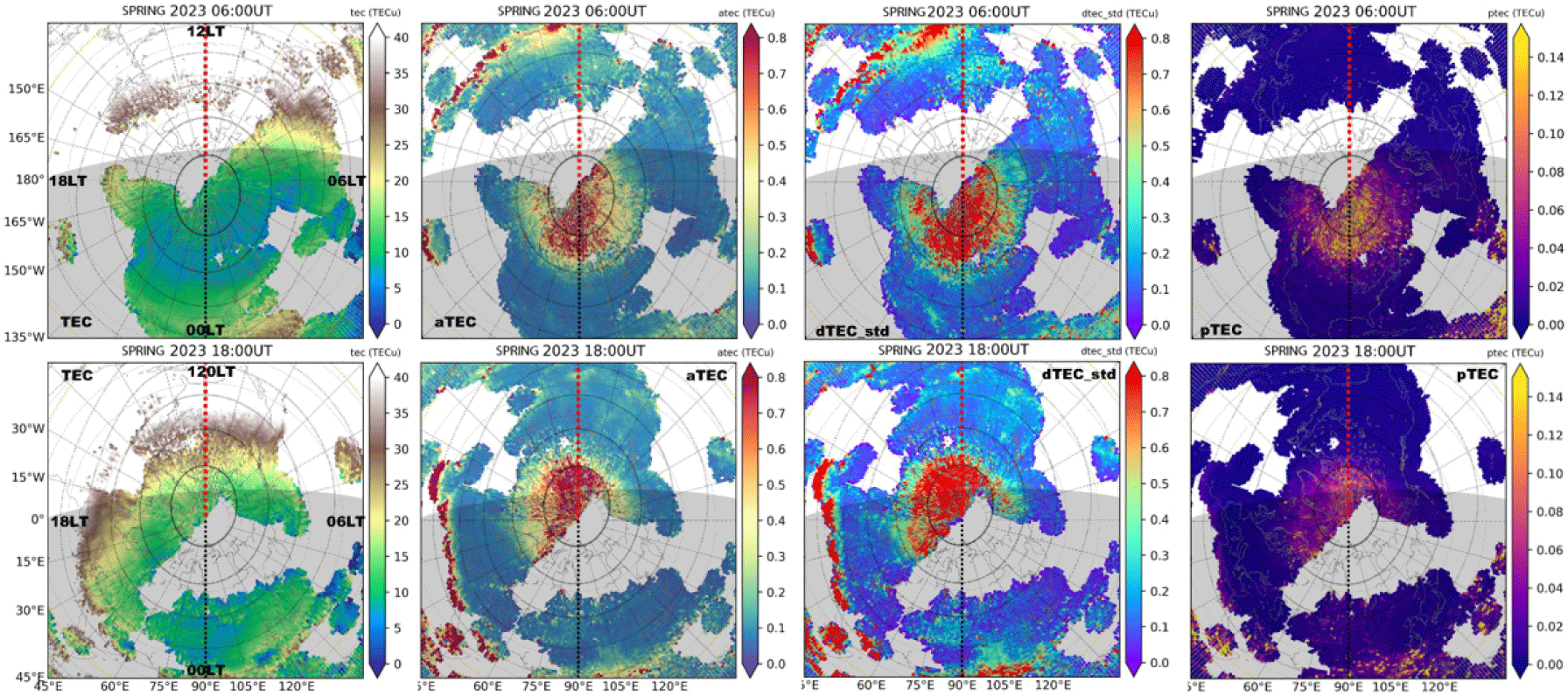
To characterize the intensity of irregularities, an additional binning step is taken in the present study. dTEC is binned into 1° longitude × 1° latitude × 5 min time bins. For each bin, an average value of |dTEC| (the absolute dTEC value), denoted as aTEC, is determined to represent the fluctuation intensity (amplitude). This bin size should be able to resolve the mean state of mesoscale fluctuations. The relative (percentage) intensity (amplitude) pTEC is defined as pTEC = aTEC/TEC, where TEC here is the bin average derived as for aTEC. The main focus of this study is to analyze these parameters at high latitudes during the period from 2010 to 2024. Fig. 2 shows TEC, aTEC, dTEC standard deviation, and pTEC obtained in the northern polar region at 0600 and 1800 UT during spring 2023. Combining data from the two UTs allows to piece together a full picture in the polar region. It is evident that aTEC and the standard deviation of dTEC exhibit similar characteristics: the dayside intense activity is bounded at ~75° apex latitudes, while the nightside intense activity is bounded at ~60°. Consequently, in our subsequent sections, we will use aTEC as proxy to quantify the intensity of irregularities.
3. RESULTS
In the following, we present the GNSS observational climatology of mesoscale irregularity at high latitudes presumably overlapping with the region of enhanced auroral activities. The aTEC averages over a given season or year as a function of UT or LT are calculated. To derive the seasonal averages from multiple-month data, daily observations are used for averaging, whereas for yearly averages, only 10-quietest days in each month are used for averaging. Section 3.4 on geomagnetic disturbance effects and Section 3.5 on solar cycle dependence show results of grouping according to the geomagnetic activity.
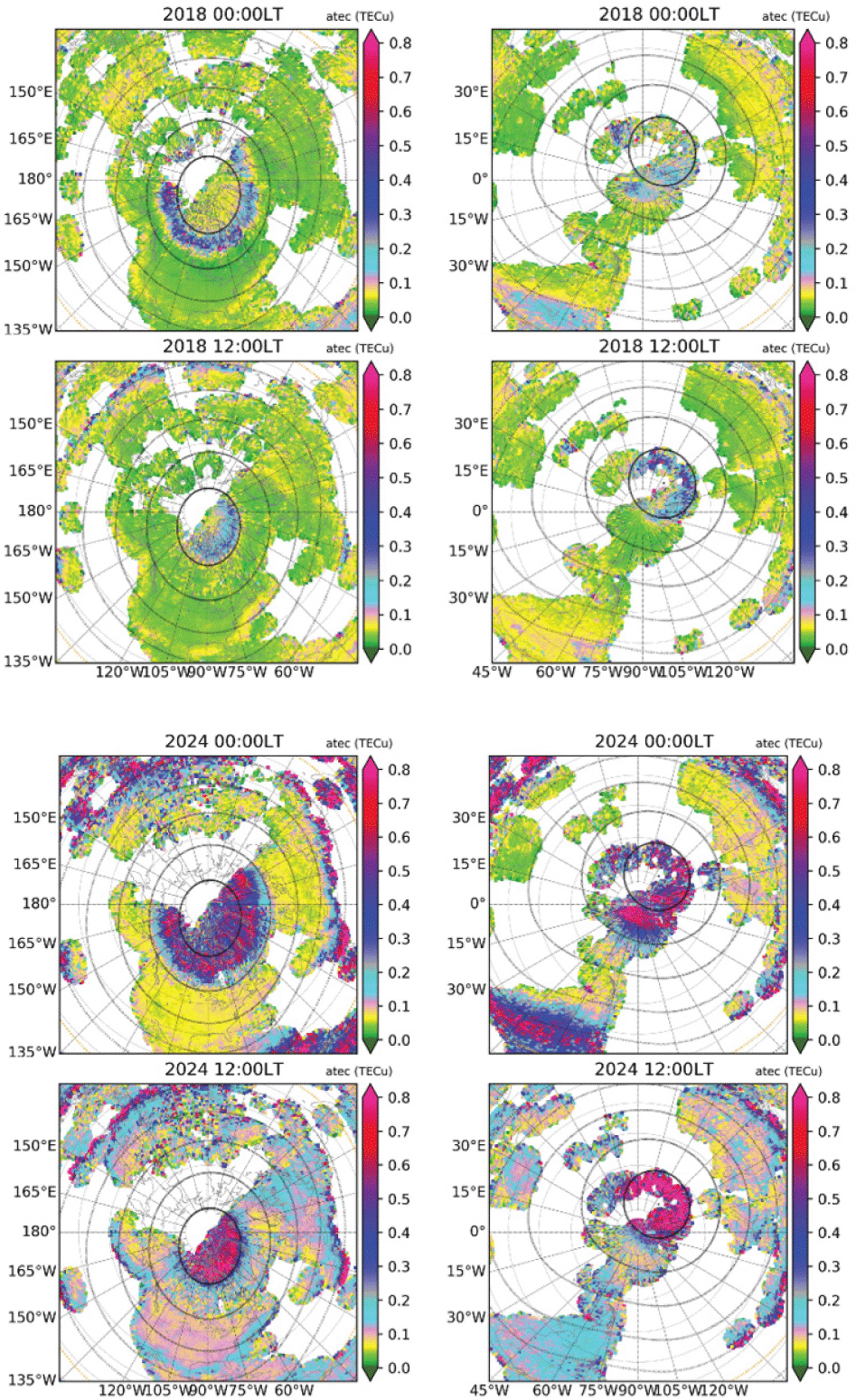
Polar views for a given UT provide snapshots of high-latitude longitudinal and latitudinal variations. Figs. 3 and 4 show yearly average patterns of UT-dependent aTEC variations in the northern hemisphere for 2024 and 2018, respectively.
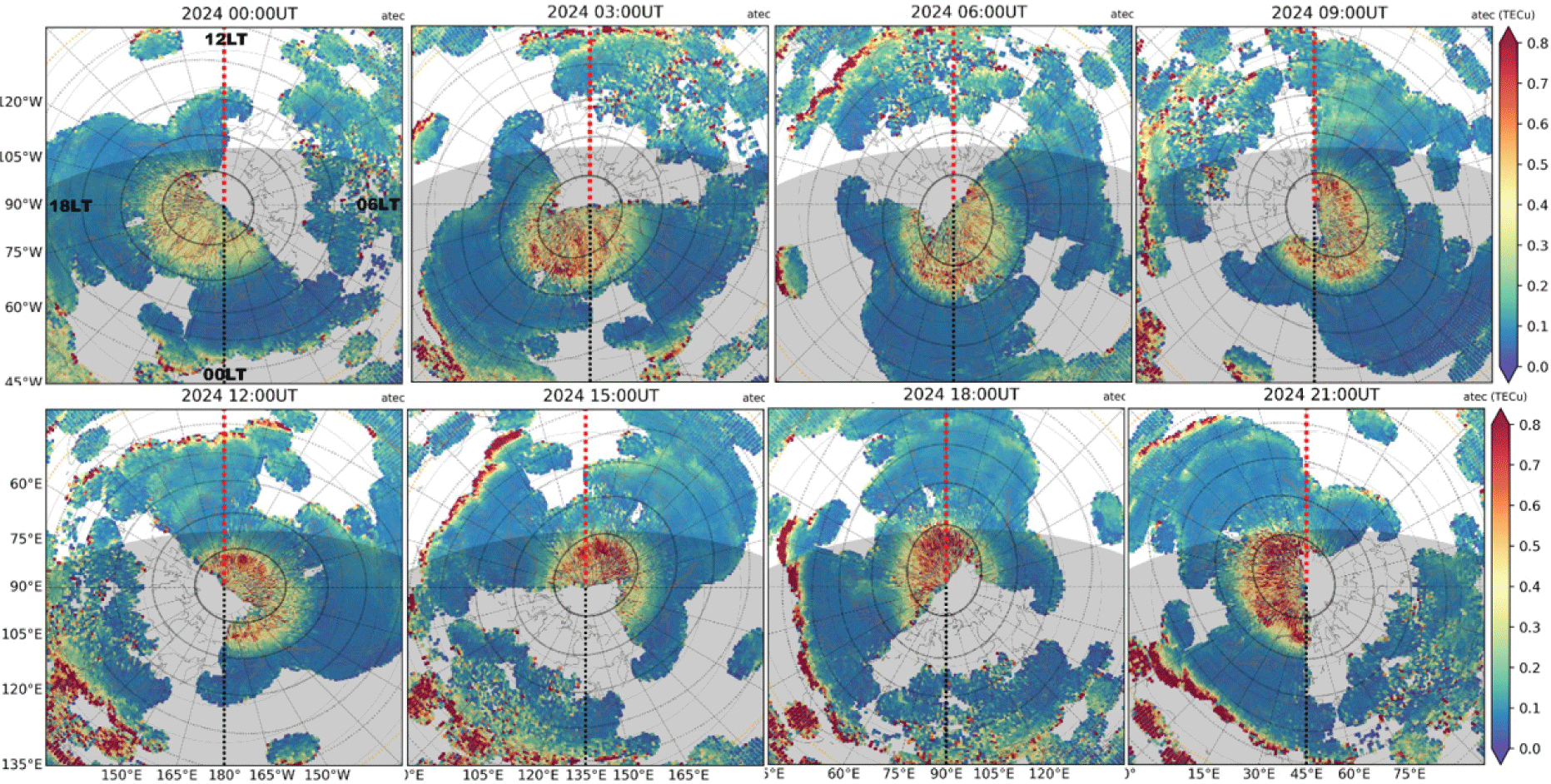
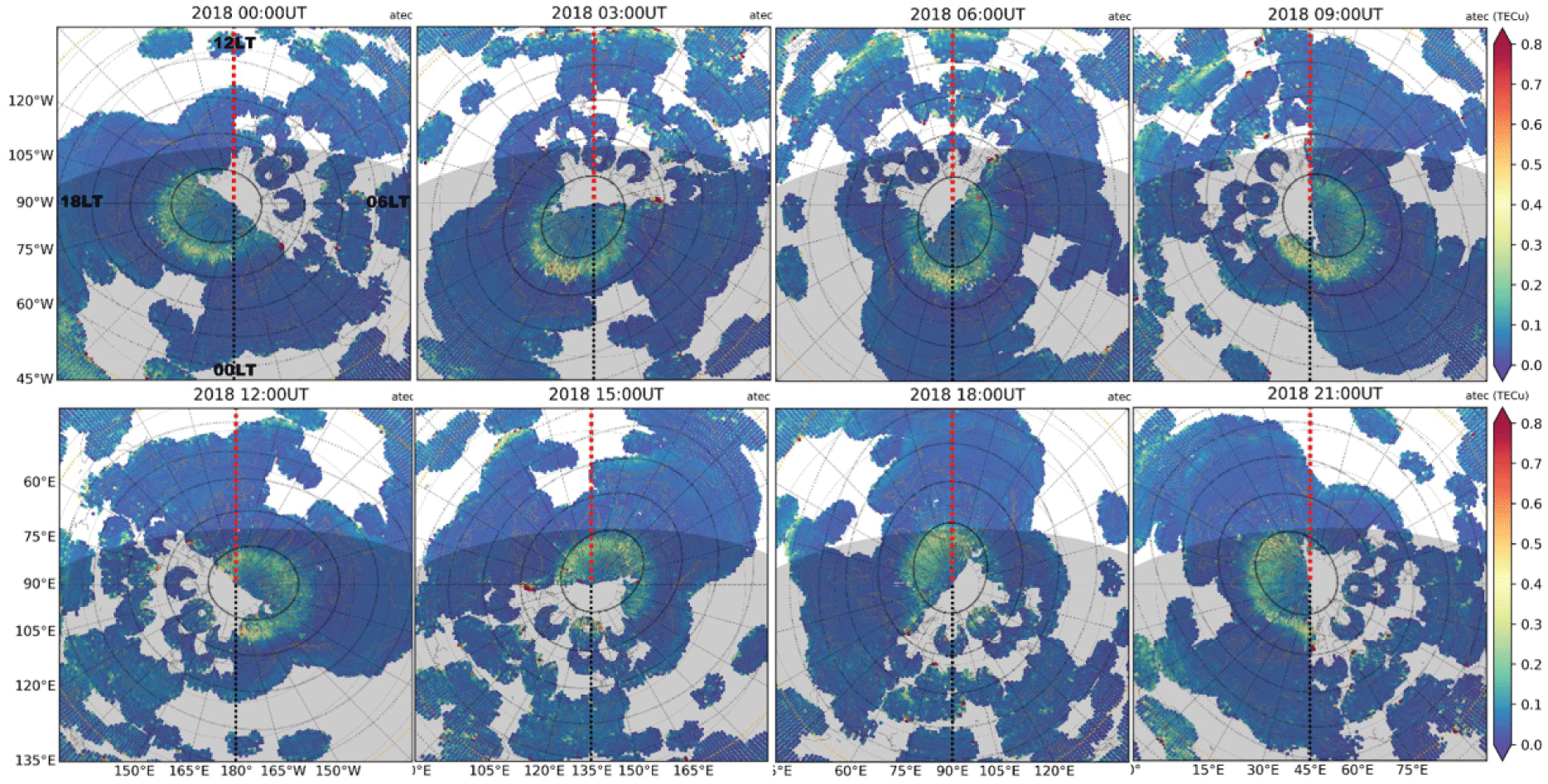
In 2024, the large aTEC (≥ 0.4 TECu) occurs within the general area of apex latitude ≥ 60°N, being closer to ≥ 75°N on dayside and extended toward ~65°N on nightside. However, some of the largest aTEC is observed near apex latitudes 67°N–68°N on nightside (0.7 TECu at 03 UT and 21 UT) and ~80°N on dayside (0.75 TECu at 15 UT and 18 UT). The dayside aTEC is generally larger than on the nightside. In 2018 during very low solar activity, however, the location of aTEC enhancement zone is similar to that in 2024, though the aTEC is generally smaller in 2018 than in 2024.
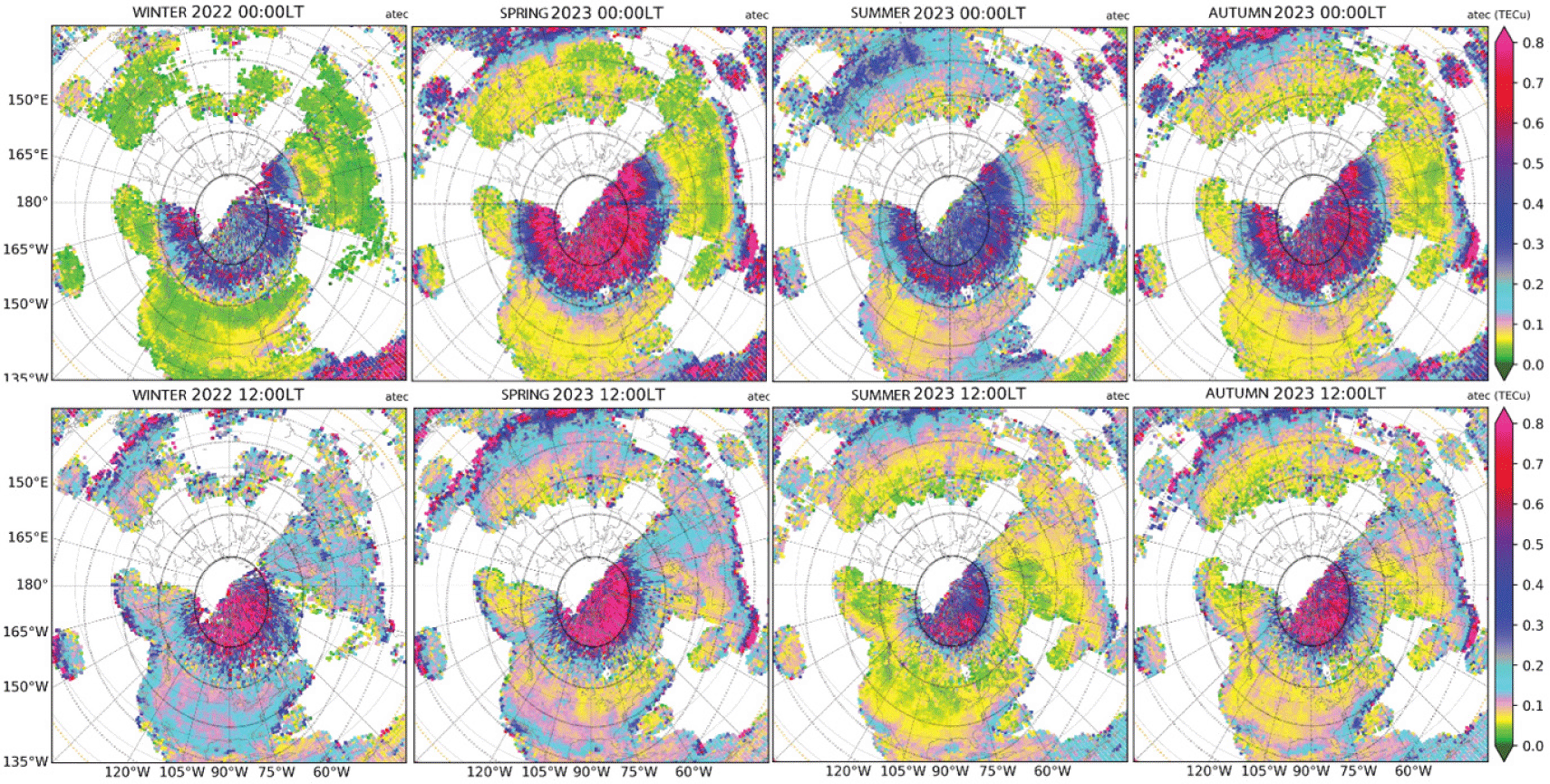
LT-dependence can be identified from Figs. 5 and 6. From 03–12 LT, the enhancement zone moves from apex latitude 65°N toward 70°N, and from 12–21 LT, it moves backwards toward lower latitudes. The same trends are developed in both low and high solar activity years 2024 and 2018, however, inside the polar cap, the enhancements during daytime hours are more evident in the high solar activity year 2024 (~0.7 TECu) than in the low solar activity year 2018 (~0.4 TECu). The nightside enhancement zones are wider in local time sectors close to the midnight for both solar activity levels.
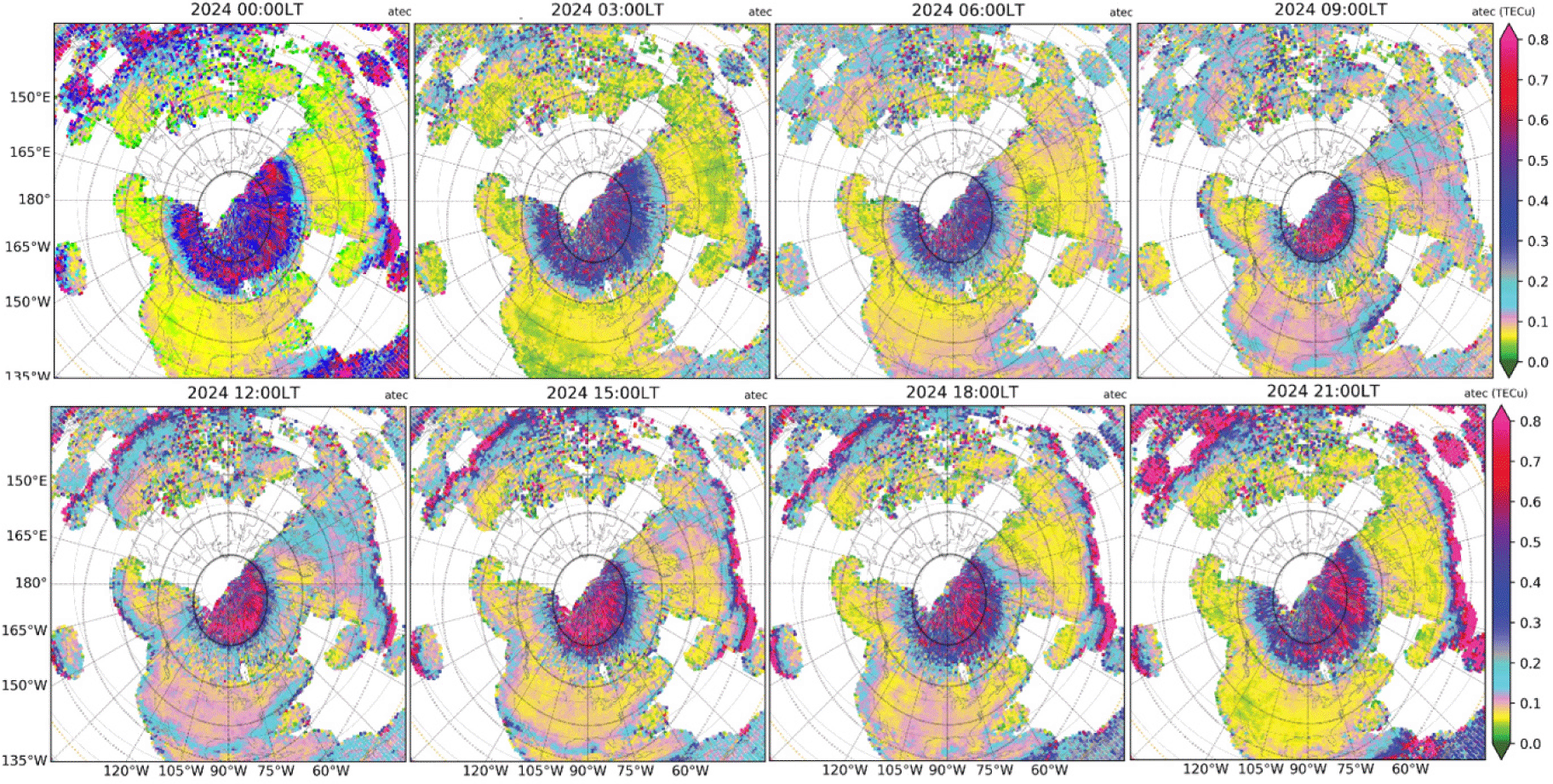
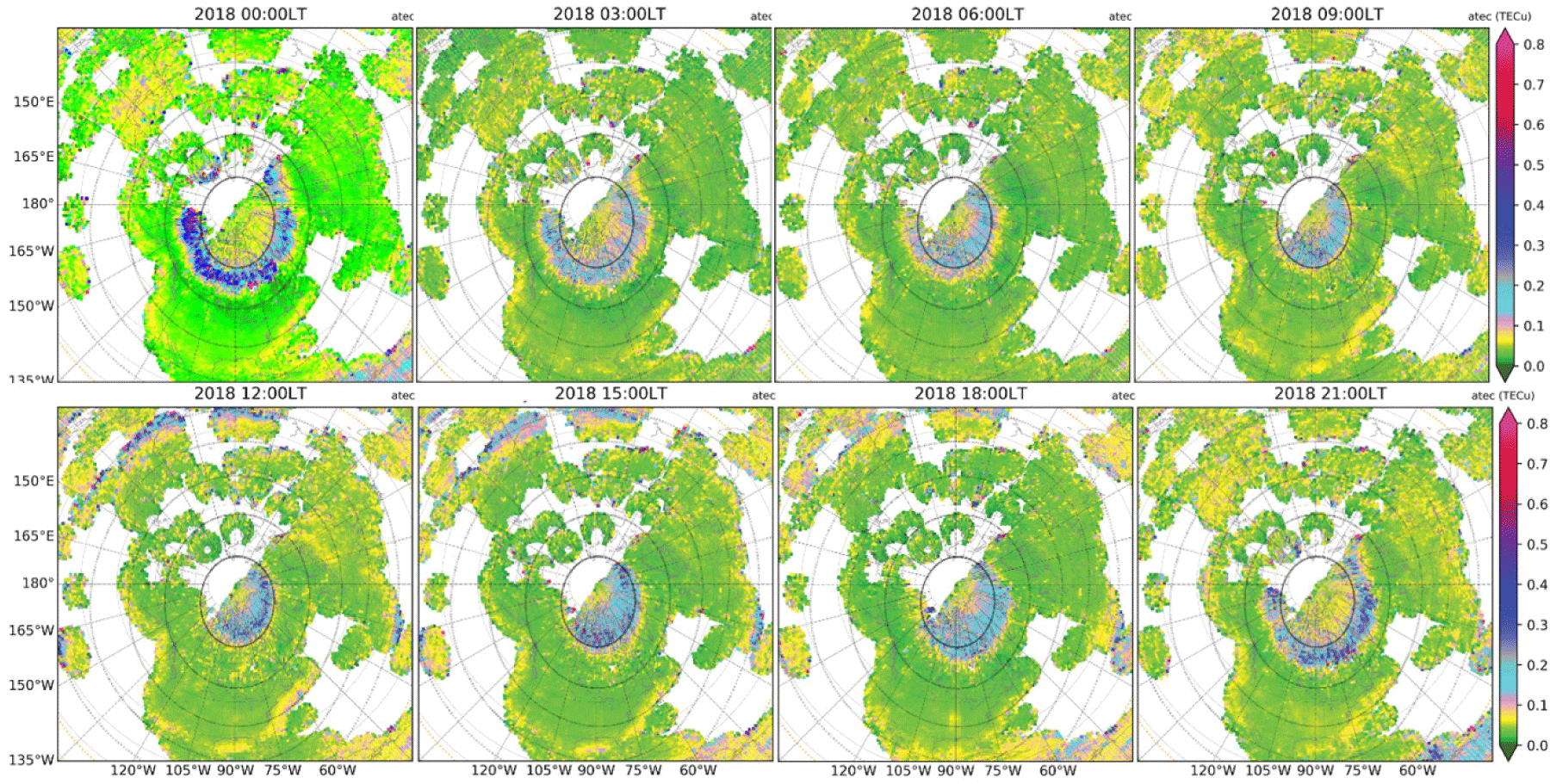
While the exact reasons for high aTEC values on the dayside and during high solar activity years remain an important question for future studies, it is worth noting the following factors: (1) the energetic particles flux can be more intense as a result of dayside reconnection; (2) the proton precipitation more likely on dayside carries more energy; (3) the magnetic field geometry can influence the precipitation efficiency; and (4) the higher conductivity on dayside and during high solar activity years can modify the magnetosphereionosphere coupling.
To evaluate the seasonal dependency of aTEC, 3-month averages centering on the equinox and solstice months, respectively, are obtained and shown in Figs. 7 and 8 for the high solar activity years between 2022–2023.
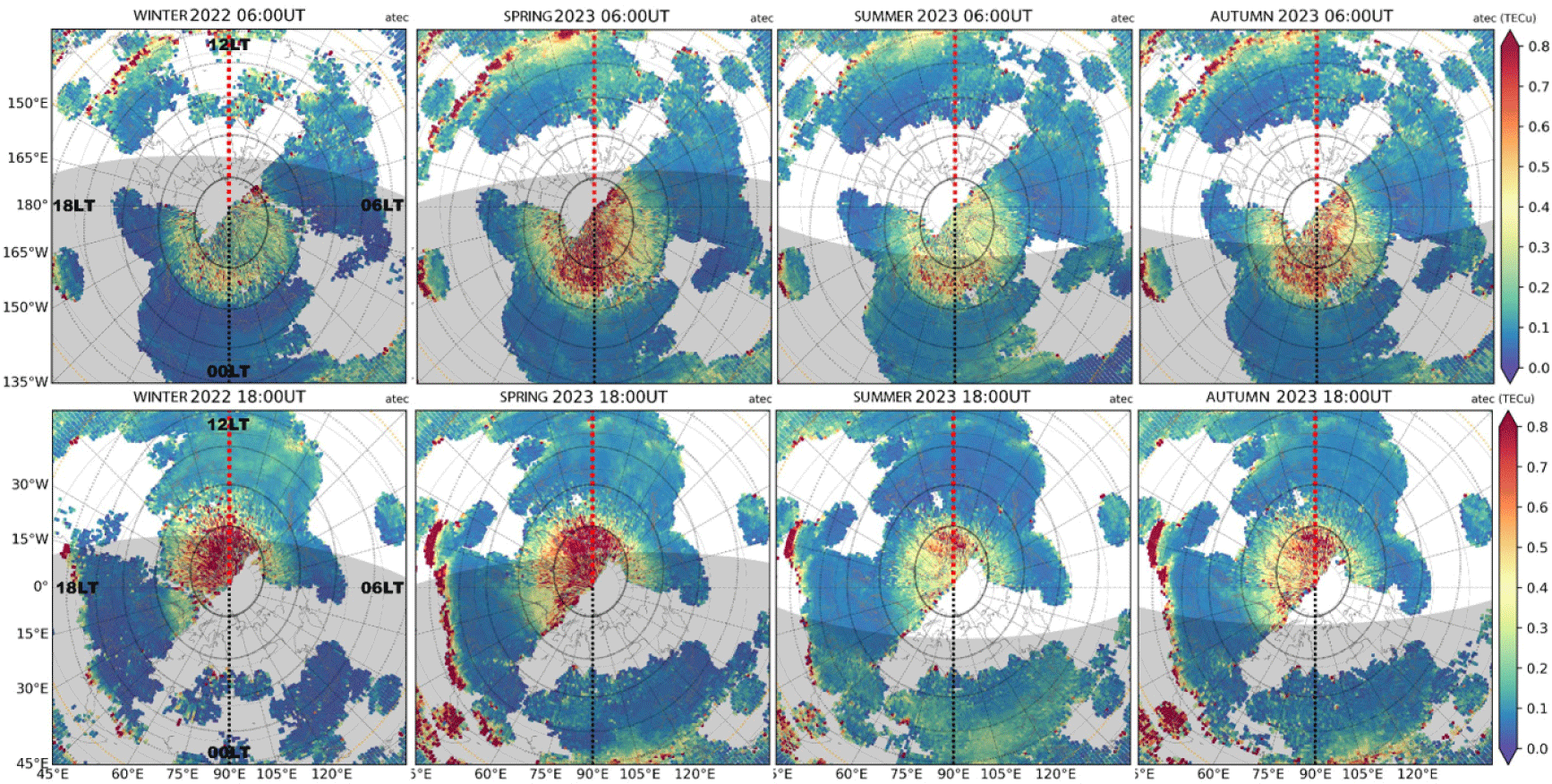
In Fig. 7, results for 06 and 18 UT provide complementary spatial coverage on both dayside and nightside. On nightside (as shown for 06 UT), although the aTEC intensity is consistently strong above apex latitude 65°N, equinox seasons exhibit higher intensities (0.7–0.75 TECu), whereas solstice seasons exhibit much weaker aTEC intensities (0.4–0.6 TECu). On the dayside (as shown for 18 UT), while aTEC intensification is consistently confined to above apex latitude 68°N, aTEC shows intensification only in the narrow noon sector at ∼0.65 TECu levels in summer and fairly so in autumn. Interestingly, in these two seasons of low intensity of irregularities, at 18 UT, the 75° apex latitude circle is entirely sunlit with large background ionospheric density.
The midnight and noon results are further compared in Fig. 8. Again, equinox seasons are characterized with higher intensity, particularly on nightside within the auroral oval and into the polar cap, with the low latitude boundary being more equatorward. Winter and summer solstices exhibit smaller aTEC. One possible explanation for the high aTEC in equinox is the stronger geomagnetic disturbance as the IMF projection onto Earth’s field lines maximizes the Bz component (Russell & McPherron 1973). On dayside, while high aTEC in equinox confines to apex latitudes > 75°N, aTEC in winter appears abnormally high. This winter dayside feature remains an interesting scientific topic for further research to clarify whether the low ionospheric conductivity leads to stronger energetic particle precipitation.
Hemispheric differences in the aTEC intensity can be observed according to LT. Fig. 9 shows these results as yearly averages for 2018 and 2024 with dramatically different solar activity levels. Although large data gaps in the southern hemisphere, general auroral oval can still be identified. The band of enhanced aTEC area is organized based on apex magnetic latitudes, with the midnight band being 10° wide starting at apex 65°N/S, and the midday band starting at apex 75°N/S. The main differences, however, lie in the aTEC intensity. At midnight, the northern hemispheric intensity in the auroral oval is considerably higher, whereas at noon, the northern hemispheric intensity in the cusp region is weaker. This is the case in both low and high solar activity years, and in the low solar activity year 2018 it is more evident.
Our statistical analysis has used all of the everyday observations in Figs 2, 7, and 8 to calculate seasonal averages, but only “international 10 quietest days” in each month in Figs. 3–6, and 9 to calculate yearly averages. In this section, we compare results obtained during “international 10 quietest days” (hereafter “quiet days”) and “international 5 most disturbed days” (hereafter “disturbed days”).
Fig. 10 demonstrates such geomagnetic disturbance effects for spring 2023 as a function of UT and LT. The results obtained on those quiet days indicate GNSS TEC responses to a background precipitation effect, which likely includes the diffuse aurora caused by wave-particle scattering in the plasma sheet, as well as other processes. These responses require a dedicated analysis. The low-latitude boundary of the auroral oval represented by aTEC activity during quiet days is confined to higher apex magnetic latitudes, being 2°–3° higher in latitude than that during disturbed days, and the intensity enhancement in aTEC during quiet days is clearly weaker and occurs more likely at higher latitudes. The high-latitude boundary of the auroral oval as seen in aTEC moves also poleward during disturbed conditions. Overall, the entire oval is expanded and activities are intensified during disturbed days. This feature will be further demonstrated in Figs. 11 and 12.

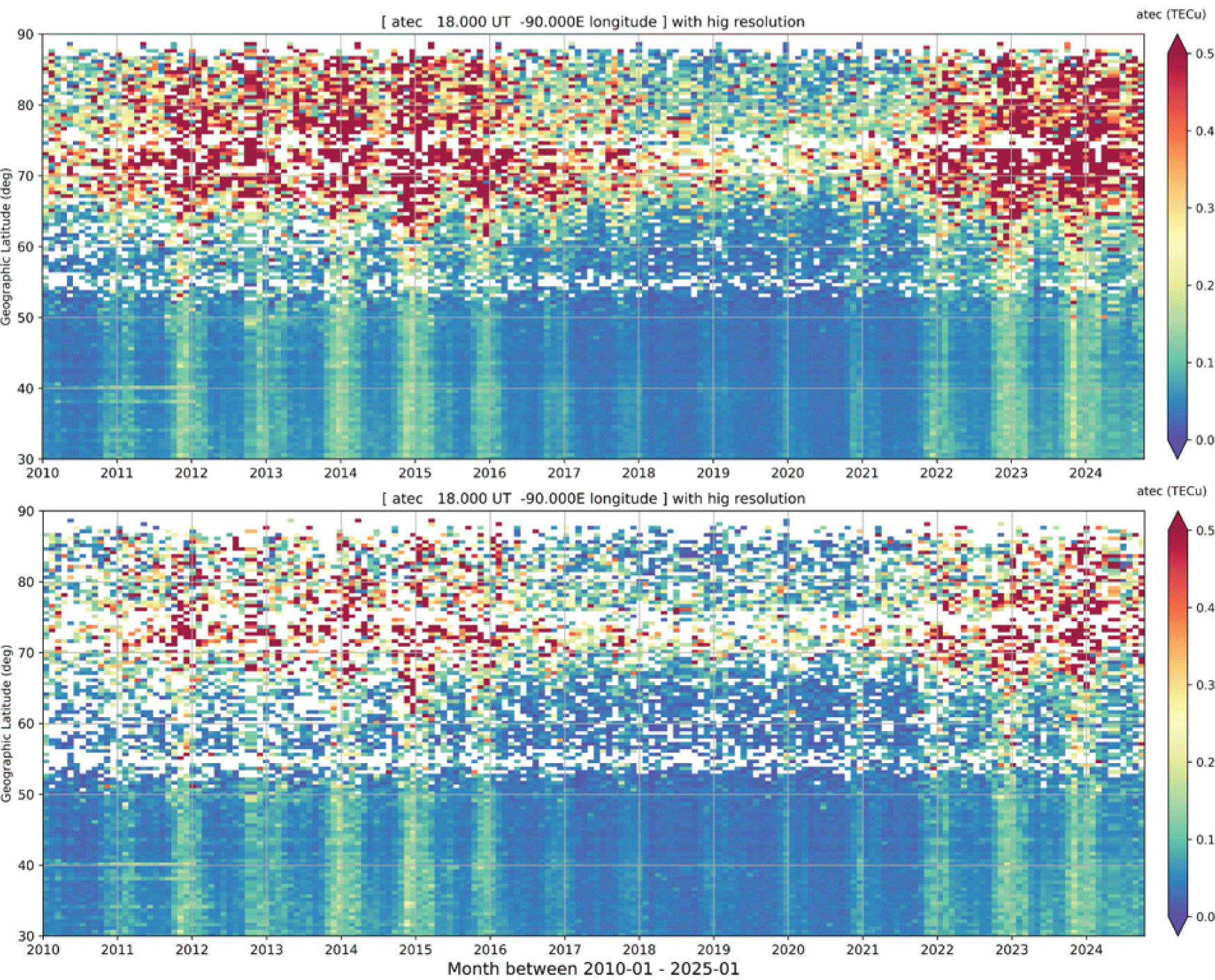

We now use observational monthly averages to demonstrate the dependency on solar cycle in the aTEC latitudinal variation at noon and midnight, respectively. These averages are calculated for the entire month (i.e., including disturbed days) and are used for comparisons with those during quiet days.
As depicted in Fig. 11 (noon) and 12 (midnight), (1) the intensity of irregularities represented by aTEC during high solar activity is higher at noon than at midnight; during low solar activity, however, aTEC is weaker at noon (< 0.3 TECu) than at midnight (> 0.4 TECu); (2) at noon, the lowlatitude boundary of the intensity enhancement is influenced significantly by solar activity, reaching a low latitude limit of 60°N (geographic) in Jan 2015, a low latitude limit of 70°N (geographic) in Jan 2020, and then back to 60°N again around Jan 2024; (3) during quiet days, this noontime lowlatitude limit varies with solar activity, following the same trend as described in (2), but the intensity of irregularities is significantly weaker for these quiet days as indicated in Section 3.4; (4) at midnight, the band of intensity enhancement within the auroral oval varies depending on the solar cycle. During high solar activity, the band is wider with its lower latitude limit extending equatorward, and during low solar activity, the band is narrower with its lower latitude limit retreating poleward; (5) during quiet days, this midnight band is much narrower with reduced intensity of irregularities (from > 0.4 TECu to < 0.4 TECu on average) within it; (6) the high-latitude limit of enhanced irregularity intensity is extended into the entire polar cap on both dayside and nightside during high solar activity, whereas during low solar activity, the irregularity oval has a much narrow latitudinal span.
The feature (6) mentioned above indicated that the intensity of mesoscale irregularities has significantly increased throughout the polar cap. As discussed in the subsequent Section, this feature is likely associated with electron density structures, such as transpolar TIDs, tongue of ionization (TOI), and polar cap patches with varying spatial sizes. These are formed during IMF Bz fluctuations and other conditions.
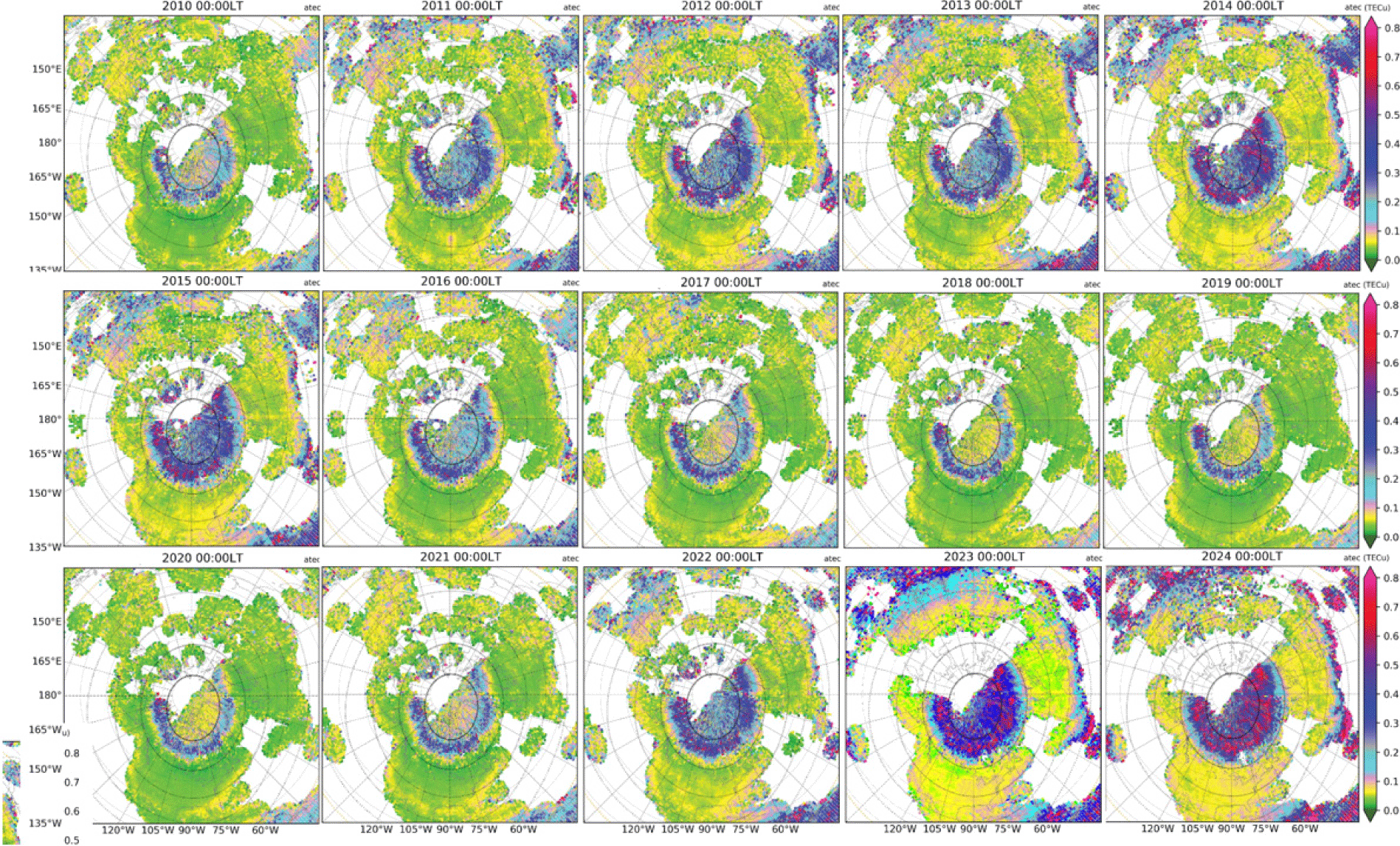
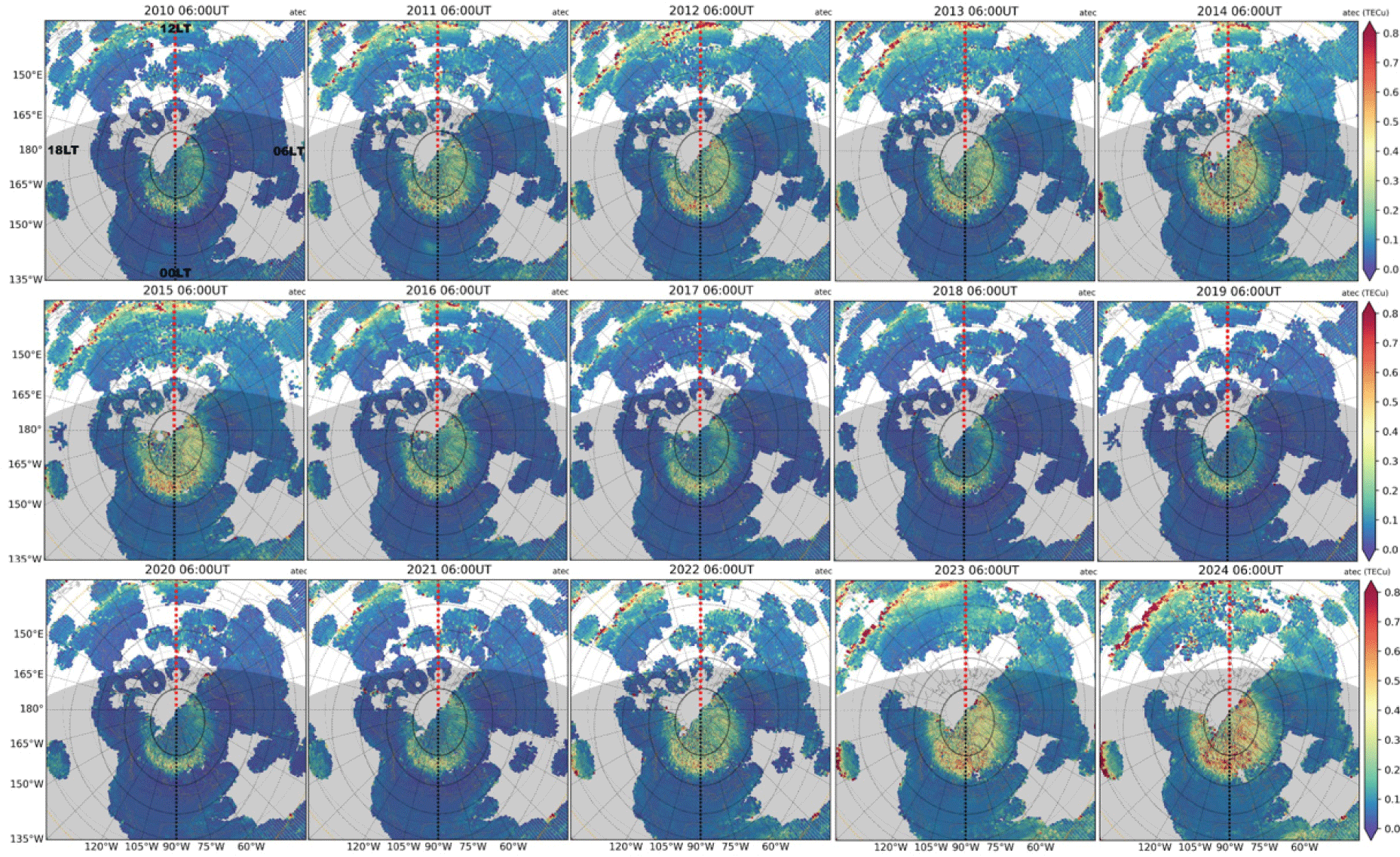
Full northern polar views are also shown in Fig. 13 (noon) and in Fig. 14 (midnight) throughout the period of 2010–2024 as yearly averages during quiet days. The solar cycle dependence of intensity of irregularities and the width of the auroral oval, which are all organized along apex latitude, is significant. Figs. 15 and 16 shows these polar maps at 06 UT and 12 UT. These UT maps show not only the intensity enhancement (auroral) locations at noon and midnight but also other local times, demonstrating the curvature changes into elliptical oval between midnight and noon.


4. DISCUSSION AND SUMMARY
This study examines ionospheric mesoscale irregularities at high latitudes, specifically those caused by energetic particle impacts on the ionospheric electron density and magnetosphere-ionosphere-thermosphere coupling processes within the auroral oval. The intensity of mesoscale irregularities is determined by using GNSS TEC observations with the TEC fluctuation component being extracted and evaluated within 1° longitude × 1° latitude × 5 min time bins. Global GNSS TEC measurements over a 15-yr period, spanning from 2010 to 2024, provide very extensive data for this analysis, resulting in a comprehensive and reliable meso-scale irregularity climatology at high latitudes.
The spatial distribution and variability of the intensity of irregularities are essentially overlapped with the auroral oval, thus the “irregularity oval” can serve as a reasonable proxy to represent the auroral oval dynamics, influenced by various factors such as local time/longitude, latitude, season, hemisphere, magnetic disturbance, and the solar cycle. Specifically, (a) the “irregularity oval” has its low latitude limit at midnight being low than at noon, and expanded equatorward during enhanced geomagnetic activity and solar activity; (b) The intensity of the irregularities appears strong on dayside than on nightside during high solar activity, and strong on nightside than on dayside during low solar activity; (c) the nightside intensity is strong in equinox than in solstices, and in summer than in winter; however, the dayside intensity is high in winter and weak in summer; and (d) during low solar activity, the intensity enhancement occurs only within the “irregularity oval” on both dayside and nightside, whereas during high solar activity, the entire polar cap throughout dayside and nightside experiences the enhanced intensity of irregularities.
The observed mesoscale irregularities represent ionospheric density structuring inside the auroral oval. While identifying the exact causes of the variability and climatology of these irregularities needs information beyond the intensity measurements, as shown here, some essential processes may be speculated. (1) Particle precipitation induced impact ionization that can influence both the E and F regions. Those associated with diffusion aurora and soft particle precipitation may lead to the F-region mesoscale irregularity. With enhanced substorm activities, the auroral zone is moved equatorward, and the auroral E may be responsible for the elevated intensity of irregularities. (2) TIDs inside the aurora and adjacent areas may be excited. LSTIDS are often observed following the Joule heating enhancement, which excites GWs in the neutral atmosphere that propagate away from the heating region into lower and higher latitudes. Some LSTIDs that propagate meridionally may constitute those mesoscale irregularities. MSTIDs has been reported to occur at subauroral latitudes arising from ionospheric instabilities due to enhanced storm-time electric field (Zhang et al. 2022; Sato et al. 2024). It is not clear how frequently these TIDs occur and what form they may take inside the auroral region. Additionally, transpolar TIDs have often been observed to travel from the dayside to nightside through the polar cap (Zhang et al. 2019b; Nishimura et al. 2020). (3) Other plasma density gradient structures, including patches and Tongue of Ionization, are also possible sources of observed density irregularities. These structures may not be precisely mesoscale any more but contribute to the observed irregularities. These can be intensified during solar wind and geomagnetic disturbances and can be observed inside the auroral oval as well as in the polar cap.
While the primary objective of this study has been to systematically document the climatology of ionospheric mesoscale irregularities, future in-depth analyses are required to quantitatively establish the relationship between the GNSS-measured “irregularity oval” and the auroral oval determined by energetic particle measurements. A subsequent step involves developing a novel GNSS TEC-based “irregularity oval” model that can account for seasonal, magnetic local time, apex latitude, and longitude variations, as well as the dependency on geomagnetic disturbance and solar activity.
