Journal of Astronomy and Space Sciences

The Korean Space Science Society

2021; 38(2):93-103

pISSN: 2093-5587, eISSN: 2093-1409

DOI: https://doi.org/10.5140/JASS.2021.38.2.93

Research Paper

Resonance Capture for a Mercurian Orbiter in the Vicinity of Sun

Elamira Hend Khattab1

, Fawzy Ahmed Abd El-Salam1^,2

, Walid A. Rahoma1^,†

¹Department of Astronomy and Space Science, Faculty of Science, Cairo University, Cairo 12613, Egypt

²Department of Mathematics, Faculty of Science, Taibah University, Madina, Saudi Arabia

^†Corresponding Author Tel: +20-002-01001084906, E-mail: rahoma@sci.cu.edu.eg

© The Korean Space Science Society. All rights reserved. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jan 23, 2021; Revised: Feb 27, 2021; Accepted: Apr 6, 2021

Abstract

In this work, the problem of resonance caused by some gravitational potentials due to Mercury and a third body, namely the Sun, together with some non-gravitational perturbations, specifically coronal mass ejections and solar wind in addition to radiation pressure, are investigated. Some simplifying assumptions without loss of accuracy are employed. The considered force model is constructed. Then the Delaunay canonical set is introduced. The Hamiltonian of the problem is obtained then it is expressed in terms of the Deluanay canonical set. The Hamiltonian is re-ordered to adopt it to the perturbation technique used to solve the problem. The Lie transform method is surveyed. The Hamiltonian is doubly averaged. The resonance capture is investigated. Finally, some numerical simulations are illustrated and are analyzed. Many resonant inclinations are revealed.

Keywords: resonance capture; merecurian gravity; third body perturbations; solar wind

1. INTRODUCTION

The resonance happens when a characterized quantity/ quantities of two/more bodies' motion is repeated at regular periods of their revolution, i.e., it is nearly commensurable, or their proportion is near to the division of a number. It can be caught easily by the presence of small divisors at equations of motion integration. The phenomena of resonance can be utilized to avoid perturbation from the gravitational potentials. The mean motion resonance between two celestial bodies means repetition of the geometrical configuration orbits periodically, which can warranty stability. Therefore, it is suitable to present an accurate and rigorous model to describe such natural interactions.

Many works are devoted to studying the resonance phenomena in celestial mechanics. The most relevant studies are Celletti (1990);Gilthorpe et al. (1990);Delhaise & Morbidelli (1993);Breiter (1999);Costa Filho & Sessin (1999);Celletti & Chierchia (2000) and Breiter (2001a, 2001b, 2003). For numerous years, scientists have accounted for the perturbation of the third body as a fundamental issue of studying the resonance problem and its behavior along the run. The readers can refer to Broucke (2003);Prado (2003) to review the problem therein. The averaging technique is usually used to address the third-body effect; see, for example, Szebehely (1964);Roth (1982);Rickman & Froeschle (1983);Ferrer & Osácar (1994) and Rahoma (2014). It still represents a topic of work, especially when the resonance and long-term perturbations are investigated as; Henrard & Caranicolas (1989);Folta & Quinn (2006);Domingos et al. (2008) and Carvalho et al. (2009a, 2009b) and discussed the lunisolar effect on Earth satellites of highaltitude using one average-model over their short-periods, while Scheeres et al. (2001) and Khattab et al. (2020) used a doubly averaged model; one over the satellite is shortperiod and the other for the third body is one. Some articles have tried to solve the problem of third perturbation, neglecting the equatorial plane inclination; Carvalho et al. (2008, 2010);Lara (2010, 2011) and Rahoma & Abd El-Salam (2014). Also the direct solar radiation pressure can modify the resonance dynamics, see for instant, Musen (1960);Cook (1962);Kozai (1963);Sehnal (1970, 1975);Anselmo et al. (1983) ; El-Saftawy et al. (1998);El-Saftawy (2005) and El- Enna et al. (2006).

Pichierri et al. (2018), Chametla et al. (2020), and Lari et al. (2020) characterized the resonant studies comparing numerical simulations and semi-analytical formulae. Also, they described the Galilean satellites' future behavior over the lifetime of the Solar System and quantified the stability of the resonance.

The insufficient information and the unclear perception about Mercury leave many important questions unsettled about the solar system's origin and its early history. Mercury has been visited only during some space missions started by flyby Mariner 10 in 1974 and 1975. The distance of Mercury from the Sun varies from 0.3 Astronomical Unit (AU) up to 0.43 AU, which raises the Sun effect on any Mercurian orbiter from the coronal mass ejections, solar wind, solar flares in addition to the Sun attraction as a third body. The nearness of Mercury's orbit for the Sun affects Mercury's space environment than those on Earth dramatically. This will lead to significant modification for the orbit of any Mercurian orbiter and has great effects on the orbiter dynamics. The phasing of the orbiter with respect to the Sun and its position in the Mercury's magnetosphere will highly affect its dynamics.

2. HIGHLIGHT ON MERCURY MISSIONS

The proximity of the planet Mercury to the Sun, as well as its small size, still represents a mystery for astronomers. Neither the ground observations nor the space ones found any evidence for an atmosphere exist at any wavelength, whether infrared, optical, or radar, which may recommend that Mercury's surface may maintain many events in the solar system history. So, the missions to Mercury were started despite its extreme difficulties, as the amount of energy required for such mission and the intercept of the spacecraft's trajectory with Venus' orbit. Lately, Venus' gravity pull was utilized to modify a mission's transfer orbit.

2.1 Mariner 10

Mariner 10 utilized Venus' gravitational attraction to reach Mercury for the first time to execute flybys of two planets in the same mission in Nov. 1973. Mariner 10 sent back different images for the sunlit hemisphere and discovered a field of dipole magnetic such that of Earth.

2.2 BepiColombo

As a dual mission in 2000, ESA and JAXA announced starting to explore Mercury; BepiColombo, by contributing to Mercury Planetary Orbiter (MPO) and Mercury Magnetospheric Orbiter (MMO), respectively. Once they orbit the planet, they will start to explore its surface and environment comprehensively. BepiColombo was started in Oct. 2018, and it will reach Mercury after seven years with modification of its trajectory by nine times.

2.3 Messenger

In August 2004, NASA launched MESSENGER to reach Mercury at polar orbit in Mar. 2011. By assisting the Earth's gravity, Venus' gravity, and Mercury itself, MESSENGER was orbited in a near-polar and highly elliptical orbit around Mercury twice every 24 hours.

There are many missions to Mercury that were planned in the present or in the future. It is helpful for such missions' design to prove the orbits from different perturbations that come from gravity or non-gravity.

The aim of this work is to highlight resonance value and investigate the resonances cases appearing due to commensurability of the mean motions of Mercury and the Sun as a third body. The objectives are located in presenting the resonant inclination behavior as a function of changing of orbital elements (argument of periapsis, eccentricity, longitude of the ascending node) at different values of the semi-major axis, i.e., the resonant inclination is the dependant variable while the orbital elements are independent variables.

3. PERTURBING FORCES MODELS

In the present work, the gravitational perturbations due to Mercury's oblateness and the Sun's gravity as a thirdbody, in addition to the non-gravitational perturbations due to Sun's coronal mass ejection, solar wind, and the solar radiation pressure, will be considered. As well as these perturbations, other forces, whether change significantly in time or random, have to add to the dynamics in further studies like Venus gravitational effects and/or Mercury's magnetic field effects, especially at Solar mass flux activity.

3.1 Assumptions

Within the accuracy respecting, the following assumptions will be introduced to simplify the dynamics sharpness.

1. The reference system center is the center of Mercury;
2. A Mercury's orbiter is considered as massless;
3. The Sun revolves in an apparent circular orbit about the Mercury, i.e. f_t + ω_t = θ, where f_t is the true anomaly of the Sun, ω_t is the periapsis argument of the Sun and θ is the mean longitude of the Sun.
4. The orbiter's motion is considered as Keplerian motion assuming the presence of the Sun's gravity and its radiation pressure as perturbing forces.
5. Suppose that the distance and the direction of the Sunorbiter are the same as that for Sun-Mercury.
6. Using the Keplerian orbital elements to characterize the orbiter's motion; a symbolizes for semi-major axis, e symbolizes for orbit's eccentricity, I symbolizes for inclination of the orbital plane due to the Mercury equatorial place, Ω symbolizes for orbit's longitude of ascending node, ω symbolizes for orbit's argument of periapsis and M symbolizes for orbiter's mean anomaly.

3.2 The Treated Gravitational Forces

The Hamiltonian of the problem can be formulated as

H G = 12 (P → ⋅ P →) − V M − V t

(1)

where $P →$ represents to canonical momentum vector, V_M and V_t represent to Mercury’s and Sun gravitational field, respectively.

Recall the Laplace’s equation ; $∇ 2 V M = 0$ , solution for a scalar function; V_M, using (r,δ,φ) as spherical coordinates on domain r > 0, 0 < δ < π, 0 ≤ φ ≤ 2π it can be expressed as a spherical harmonics infinite series, Arfken (2012).

Let the gravitational field of Mercury is an axially symmetry, where the axes origin is located at its center of mass, then the scalar function can be written as V_M; see for instant Fitzpatrick (1970)

V M = − μ M r + μ M r ∑ n = 2 ∞ (R M r) n J n P n (sin δ) − 3 μ M 4 r (R M r) 2 J 22 × {2 S 2 cos (2 Ω − 2 τ) + (cos I + 1) 2 cos (2 f + 2 ω + 2 Ω − 2 τ) + (cos I − 1) 2 cos (2 f + 2 ω + 2 Ω − 2 τ)}

(2)

where μ_M is the Mercury’s gravitational parameter, R_M is the Mercury’s equatorial radius, J_n are the zonal harmonic coefficients, J₂₂ is the first tesseral harmonic, (r,δ) are the orbiter coordinates as appeared from Mercury’s center, P_n(sinδ) represent the Legendre Polynomials, f defined the true anomaly and finally, τ is standed for the Mercurian reference sidereal time.

To simplify the writing, let us use S = sinI, C = cosI, $F i . j m = i f + j ω + m Ω$ and $sin δ = S sin F 1, 1 0$ , Abd El-Salam et al. (2006) and Rahoma et al. (2014).

3.2.1 Third Body Perturbation

The perturbation due to the third body is given by

V t = μ t Θ 2 a t 3 r t ∑ k = 2 ∞ (r r t) k P k (cos ψ)

(3)

where μ_t = GM_t,ψ symbolizes to the Sun-Orbiter angle from the Mercury, $r →$ is the position of orbiter relative to Mercury, M_t is the Sun's mass, and G symbolizes to the gravitational constant. Θ symbolizes to the mean motion of the Sun, for a_t symbolizes to the semi-major axis of the Sun's orbit as it appear from Mercury. For the model, retaining the disturbing function P₂ and P₃ (R₂ and R₃) in the summation yields;

V t = R 2 + R 3

(4)

where

R 2 = μ t Θ 2 a 2 2 (a t r t) 3 (r a) 2 3 cos ψ 2 − 1,

(5)

R 3 = μ t Θ 2 a 3 2 r t (a t r t) 3 (r a) 3 5cos ψ 3 − 3 cos ψ,

(6)

where cosψ can be expressed as

with

α = cosω cos(Ω – f_t – ω_t) – cosI sinω sin(Ω – f_t – ω_t),
β = –sinω sinω cos(Ω – f_t – ω_t) – cosI cosω sin(Ω – f_t – ω_t)

Adopted from Abd El-Salam (2007) with permission of Elsevier.

3.3 The Solar Radiation Pressure Effect

All objects in the solar system suffer from the sun’s radiation force that is called solar radiation pressure especially those at closer distances from the Sun. Solar radiation pressure significantly affects the smaller bodies as their surface area to mass ratio (A_i / m) are large somewhat unless their orbital position lies in the orbited body shadow. The orbital elements are periodically changed as a result of this force. In view of the assumptions, the surface elements contribution to total acceleration can be formulatted as:

F → S R = − A i m S 0 c l (a M − s a) cos γ i (1 − β i) s^

(7)

where S₀ = 1,370 W/m² symbolizes to the solar constant (identical to the average distance of Mercury-Sun a_M–s) Lewis (2004), γ_i symbolizes to the incidence angle, β_i symbolizes to the coefficient of reflection for i^th orbiter’s surface and $s^$ symbolizes to the unit vector of Orbiter-Sun direction, where the reference frame is the Mercurocentric equator, and it can be written as

s^= cos θ i^+ cos ε sin θ j^+ sin ε cos θ k^

where θ(= Θt)t symbolizes to time, and ε symbolizes to the obliquity (Mercurian equator plane with respect to the ecliptic).

3.4 The Coronal Mass Ejections and Solar Wind Effects

Solar mass ejects protons to the surrounding space due to solar wind, solar flares and corona mass ejection. Actually, solar wind is the most important force in this ejection. Typically at Earth, solar wind speed nearly 400 km/s, Breen et al. (2002) and its density nearly 10 protons/cm³. On other hand, thanks Mariner 10, at Mercury solar wind speed nearly 423 km/s while its density nearly 60 protons/cm³.

Assume that the Mercurian orbiter is impacted by inelastic particles and the angular span of ejections are spherical envelope, The solar wind perturbing acceleration and coronal mass ejections perturbing acceleration can be formulated, respectively, as, see Abd El-Salam (2007),

F → s w = (A i m) s w n s w M P v s w 2 s^

(8)

F → C M E = (A i m) C M E M C M E V C M E v C M E 2 s^,

(9)

where(A_i / m)_SW defined area-mass ratio which exposed to solar wind, n_SW symbolizes to particle density, υ_SW symbolizes to solar wind velocity, and M_P is the proton mass, While (A_i / m)_CME defined area-mass ratio which exposed to coronal mass ejection , V_CME symbolizes to the volume, M_CME symbolizes to the mass and υ_CME symbolizes to coronal mass ejections velocity.

4. CANONICAL FORMULATION AND ORDERING

Selecting Delaunay variables as canonical ones which can be defined as

l = M L = μ M a g = ω G = L 1 − e 2 h = Ω H = G cos I

Now to insert the forces $F → S R, F → S W, and F → C M E$ into the problem’s Hamiltonian as a adopted solution technique, they would be rewritten as a gradient for combined function (let Φ_⊙) i.e.

F → ⊙ = F → S R + F → S W + F → C M E = (R S R + R S W + R C M E) s^

(10)

F → ⊙ = − ∂ Φ ∂ r →

(11)

where $R S R = − A i m S 0 c l (a M − s a) cos γ i (1 − β i), R S W = (A i m) S W n S W M P v S W 2$ and $R C M E = (A i m) C M E M C M E V C M E v C M E 2$

To obey equation (11),

Φ ⊙ = − F → ⊙ ⋅ r → = (R S R + R S W + R C M E) (s^⋅ r →)

(12)

where $F → ⊙$ is an explicitly time dependence within the Sun’s mean longitude θ(= Θt).

To recover equations autonomous, a new conjugate pair of variables; (k,K), will be setted to Delaunay variables where k = Θt + const.

Utilizing the extended Delaunay variables, the Hamiltonian of the three forces can be formulated as

H ⊙ s = Θ K + Φ ⊙

(13)

with

Φ ⊙ = 14 (R S R + R S W + R C M E) L 2 (a r) − 1 ∑ m = − 1 1 ∑ n = − 1 1 C m, n F m, n

where F_m,n = f + g + mh + nk.

The non-vanishing coefficients for C’s are

C 1. − 1 = (1 + C) (1 + C ε), C 1.1 = (1 + C) (1 − C ε), C − 1, 1 = (1 − C) (1 + C ε), C − 1, − 1 = (1 − C) (1 − C ε), C 0, − 1 = 2 S S ε, C 0, 1 = − 2 S S ε

with C_ε = cosε, S_ε = sinε

5. ASSESSMENT OF THE ORDERS OF MAGNITUDE

The magnitude orders φ(x),x = 1,2,… in view of a small parameter; ∈ for perturbing terms can be clarified as, see Abd El-Salam (2007),

∈ X ∈ ≤ φ (X) ≤ ∈ (X − 1) ∈

In our problem, the Mercurian coefficients J₂ ≃ C₂₂ is considered as a first order. Also the orbiter’s mean motion around Mercury varies from 2,500 rev./day up to 100 rev./ day. Also, the solar mean motion Θ ≅ 0.1 rev./day. i.e, R2 is considered as of the first order. Finally, J₃, J₄, J₅ are are considered of the second order.

Now the magnitude order for each considered nongravitational force is determined by a single nominal magnitude which is

F → S R = 1.488 × 10 − 6 (m / s 2), (r / r ′) 2 = 2.7 × 10 − 7 F → S W = 3.773 × 10 − 8 (m / s 2), F → C M E = 3.726 × 10 − 10 (m / s 2)

Therefore, truncating the series of the Mercurian gravitational potential up to J₅, the perturbing Hamiltonians (1) can be written as, Abd El-Salam et al. (2006):

H = ∑ n = 0 2 J 2 n n! H n

(14)

with

H 0 = − μ n 2 2 L 2 + Θ K

(15)

H 1 = A 12 z 4 L 6 (a r) 3 [(3 S 2 − 2) − 3 S 2 cos 2 (f + g)] + 3 A 12 s 4 L 6 (a r) 3 [2 S 2 cos (2 h) + (C + 1) 2 cos 2 (f + g + h) + (C − 1) 2 cos 2 (f + g − h)] + B S R L 2 (a r) − 1 ∑ m = − 1 1 ∑ n = − 1 1 C n, m cos F m, n + A 1 t a 2 (a t r t) 3 (r a) 2 [3 (α cos f + β sin f) 2 − 1]

(16)

H 2 = A 23 8 L 8 (a r) 4 [(15 S 3 − 12 S) sin (f + g) − 3 S 3 sin3 (f + g)] + A 24 64 L 10 (a r) 5 [(105 S 4 − 120 S 2 + 24) − (140 S 4 − 120 S 2) cos 2 (f + g) + 35 S 4 cos 4 (f + g)] + A 25 128 L 12 (a r) 6 [(630 S 5 − 840 S 3 + 240 S) sin (f + g) - (315 S 5 − 280 S 3) sin3 (f + g) +36 S 5 sin 5 (f + g)] + (B C M E + B S W) L 2 (a r) − 1 ∑ m = − 1 1 ∑ n = − 1 1 C n, m cos F m, n + A 2 t a 3 (a t r t) 3 (r a) 3 [5 (α cos f + β sin f) 3 − 3 (α cos f + β sin f)]

(17)

where the dimensionless quantities are defined as:

A 12 z = μ M 4 R M 2, A 12 s = J 22 J 2 μ M 4 R M 2, B S R = R S R 4 J 2, A 1 t = μ t Θ 2 2 J 2, A 2 t = μ t Θ 2 J 22, A 23 = 2 J 3 J 22 μ M 5 R M 3, A 24 = 2 J 4 J 22 μ M 6 R M 4, A 25 = 2 J 5 J 22 μ M 7 R M 5, B C M E = R C M E 4 J 22, B S W = R S W 4 J 22 .

6. METHODOLOGICAL TECHNIQUE

Lie transforms method; initially developed for vector fields by Deprit (1969) and Kamel (1969), and others, is a powerful procedure to deal with a perturbed Hamiltonian depending on a small parameter. This method allows recursive routines to transform the original system perturbation to another one which features by flexiable properties.

Let the Hamiltonian of a problem be a function of canonical variables (the coordinates and momenta) i.e. $K q, Q$ , the motion equations can be formulated as:

q ˙ = ∂ K ∂ Q, Q ˙ = − ∂ K ∂ q

In a problem, considering a small parameter; ε, and the Hamiltonian $K$ may be expand as:

K = K 0 + ∑ n = 1 ε n n! K n

where $K 0$ is the unperturbed Hamiltonian (integrable part).

To improve the solution considering the perturbing Hamiltonian $K n$ , a one /or more canonical transformations analytic in ε at ε = 0 is required to remove the fast and slow angles from $K n$ respectively.

The transformed Hamiltonians and its corresponding generators can be formulated as:

K * (−, q ′ 2, q ′ 3, Q ′; ε) = K 0 * (Q ′) + ∑ n = 1 ε n n! K n * (−, q ′ 2, q ′ 3, Q ′) W 1 (q ′, Q ′; ε) = ∑ n = 0 ε n n! W n + 1 (q ′, Q ′)

Clearly from the described technique to deal with the our perturbed Hamiltonian H(l, g, h, k, L, G, H, K; J₂), we have to do two canonical transformations to eliminate:

1- two fast variables namely the orbiter’s mean anomaly l in addition to the solar mean longitude k to be H*(–, g, h, –, L, G, H, K; J₂).
2- two slow variables, g, h to be H**(–, –, –, –, L, G, H, K; J₂). The first averaging process yields

$H * = ∑ n = 0 2 J 2 n n! H n *$
(18)

with

H 0 * = − μ n 2 2 L 2 + Θ K

(19)

H 1 * = A 12 z 4 L 3 G 3 (1 − 3 H 2 G 2) + 6 A 12 s 4 L 3 G 3 (1 − H 2 G 2) cos (2 h) + K 1 L 2 [(5 − 3 G 2 L 2) (3 H 2 G 2 − 1) + 15 (1 − G 2 L 2) (1 − H 2 G 2) cos (2 g)]

(20)

with

K 1 = μ t Θ 2 16 μ M

and the second averaging process yields

H * * = ∑ n = 0 2 J 2 n n! H n * *

(21)

with

H 0 * * = − μ n 2 2 L 2 + Θ K

(22)

H 1 * * = A 12 z 4 L 3 G 3 (1 − 3 H 2 G 2) + K 1 L 2 [(5 − 3 G 2 L 2) (3 H 2 G 2 − 1)]

(23)

The corresponding generator can be written in the form

W = ∑ p = 0 1 ∑ m = 0 1 B 0, 2 p m, 0 2 p ∂ (H 1 * + H 1 * *) ∂ G + m ∂ (H 1 * + H 1 * *) ∂ H sin F 0, 2 p m, 0

where $B 0, 2 p m, 0$ are functions in momenta only.

7. RESONANCE CAPTURE

Suppose a periodic mechanical system has a number of natural frequencies.Whenever two or more of these frequencies are nearly commensurable, resonance arises. Simply this may be formulated n₁ / n₂ = p / q where n₁ and n₂ are the two natural frequencies and p and q are small prime integers.

The theoretical problem in cases of near commensurability motion is due to the small divisors appearance in the developments of the usual asymptotic representations of the solution. These divisors have the form pn₁ – qn₂, leading to an unsatisfactory solution.

In celestial mechanics theses problems type present themselves clearly. Like the Earth’s satellite critical inclination as a result of near-commensurability of draconic and the anomalistic frequencies. In addition,the mean motion of an artificial satellite may be commensurable with the angular velocity of the primary body.

The resonance cases will be created when the denominators generating function become sufficiently small or vanish. These conditions can be formulated as:

2 p ∂ (H 1 * + H 1 * *) ∂ G + m ∂ (H 1 * + H 1 * *) ∂ H = 0

(24)

where

H 1 * + H 1 * * = A 12 z 2 L 3 G 3 (1 − 3 H 2 G 2) + 6 A 12 s 4 L 3 G 3 (1 − H 2 G 2) cos (2 h) + K 1 L 2 [2 (5 − 3 G 2 L 2) (3 H 2 G 2 − 1) + 15 (1 − G 2 L 2) (1 − H 2 G 2) cos (2 g)]

and

∂ (H 1 * + H 1 * *) 2 G = 3 A 12 z 2 L 3 G 6 (− G 2 + 5 H 2) − 3 A 12 s 2 L 3 G 6 (3 G 2 − 5 H 2) cos (2 h) + K 1 [12 G − 60 H 2 L 2 G 3 − 30 (G − H 2 L 2 G 3) cos (2 g)] ∂ (H 1 * + H 1 * *) ∂ H = − 3 H L 3 G 5 (A 12 z + A 12 s cos (2 h)) + K 1 [12 H (− 3 + 5 L 2 G 2) + 30 (G 2 − L 2) G 2 cos (2 g)]

If we substitute H = Gcos I in the equation (24), we get a quadratic function in the inclination as:

γ 0 + γ 1 cos I + γ 2 cos I 2 = 0

(25)

The solution (25) yields the different resonant inclinations as

I 1, 2 = cos − 1 (− γ 1 ± γ 12 − 4 γ 2 γ 0 2 γ 2)

where

γ 0 = p [A 12 z + 3 A 12 s cos (2 h) − 4 K 1 G 5 L 3 (2 − 5 cos (2 g))] γ 1 = m [A 12 z + A 12 s cos (2 h) + 2 K 1 G 3 L 3 (6 G 2 − 10 L 2 − 5 (G 2 − L 2) cos (2 g))] γ 2 = − 5 p [A 12 z + A 12 s cos (2 h) − 4 K 1 G 3 L 5 (2 − cos (2 g))]

8. OUTCOME SIMULATIONS

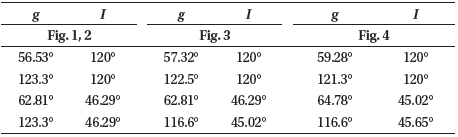
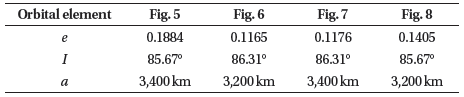
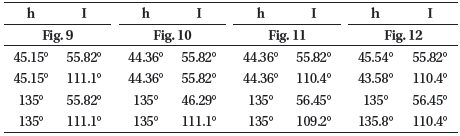
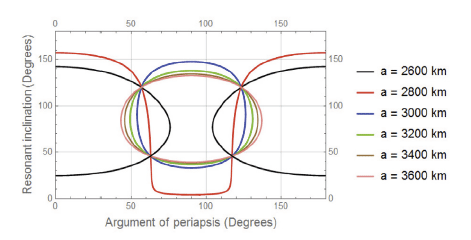
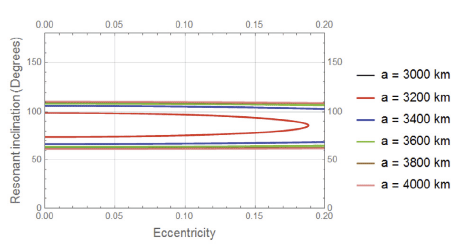
In this section, the behaviour of the resonant inclination is investigated as a function of orbital elements. A following mercurian data are imposed in the simulations, Semi-major axis; a_M = 5.791 × 10⁷ km, Eccentricity e_M = 0.205, Orbital period is 87.969 days, Inclination; I = 7.0°, Longitude of perihelion, ω = 77.46°, Longitude of ascending node, Ω = 48.33° and Orbit Obliquity is 0.1°. In addition to, Mercury’s Mass M_M = 3.302 × 10²³ km, R_M = 2,439 km, μ_M = 0.02203 × 10⁶ km³s^–2, J₂ = 60 × 10^–6 and J₂₂ = 10 × 10^–6. In the light of equation (25) we can treat the resonant inclination as a dependant variable and the orbital elements as independent variables. In each case study we will fix all orbital elements except that element we need to observe the behaviour of the resonant inclination under its change. In each figure we have fixed two orbital elements, see each figure caption. Also different colored curves are plotted in each figure, each color corresponds to a specified value of the semi-major axis as shown in the legend attached to the right of the diagram.

8.1 Resonance Analysis Versus the Argument of Periapsis

In this case we study the behaviour of the resonant inclination in degree in terms of changing the argument of periapsis.

8.1.1 Analysis of Figs. -

It is observed that all curves in Figs. 1–4 meet at two resonant inclinations, a relatively small perturbations in these inclinations are observed. These results can be summerized in the following Table 1.

Fig. 1. The resonant inclination dynamics versus the argument of periapsis, Ω = 90˚, e = 0.

Download Original Figure

Fig. 2. The resonant inclination dynamics versus the argument of periapsis, Ω = 90˚, e = 0.1.

Download Original Figure

Fig. 3. The resonant inclination dynamics versus the argument of periapsis, , Ω = 90˚, e = 0.15.

Download Original Figure

Fig. 4. The resonant inclination dynamics versus the argument of periapsis, , Ω = 90˚, e = 0.2.

Download Original Figure

Table 1. Resonant inclinations versus argument of periapsis

Download Excel Table

8.2 Resonance analysis versus the eccentricity

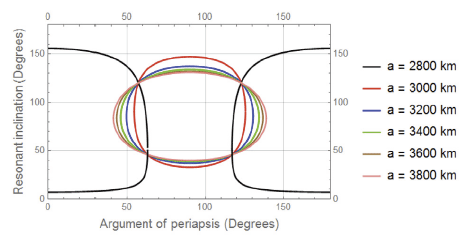
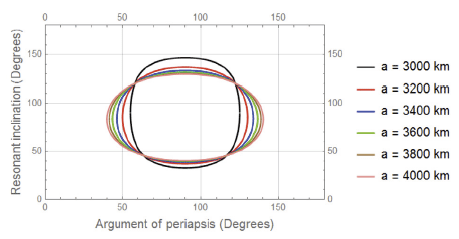
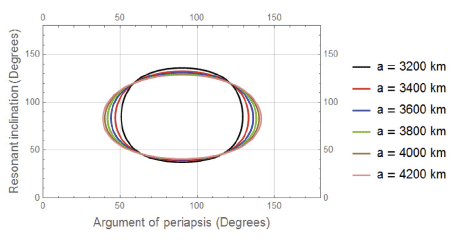
In this case we study the behaviour of the resonant inclination in degree in terms of changing the eccentricity Figs. 5–8. The dynamics is simple. Each case is relatively represented by constant linear function except at the semimajor axis equal 3,200 km and 3,400 km. The dynamics in these two cases are also approximately linea form e = 0 to about e = 0.1 and beyond that it bahaves nonlinearly, the two roots meet at the following values, see Table 2.

Fig. 5. The resonant inclination dynamics versus the eccentricity, Ω = 60˚, ω = 45˚.

Download Original Figure

Fig. 6. The resonant inclination dynamics versus the eccentricity, Ω = 62˚, ω = 45˚.

Download Original Figure

Fig. 7. The resonant inclination dynamics versus the eccentricity, Ω = 72˚, ω = 45˚.

Download Original Figure

Fig. 8. The resonant inclination dynamics versus the eccentricity, Ω = 74˚, ω = 45˚.

Download Original Figure

Table 2. Resonant inclinations versus eccentricity and semimajor axes

Download Excel Table

8.3 Resonance Analysis Versus the Longitude of the Ascending Node

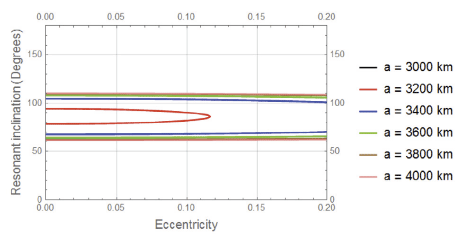
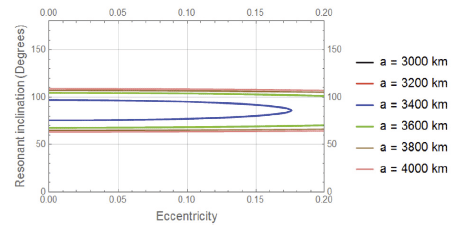
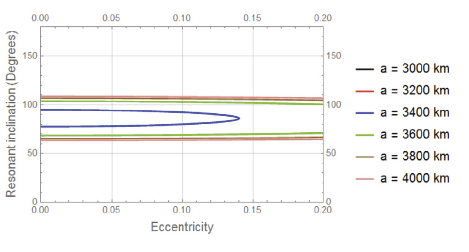
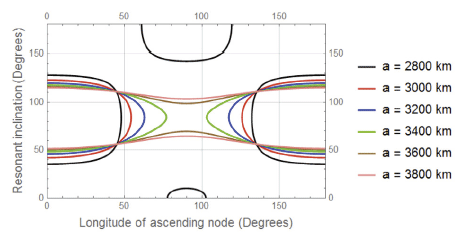
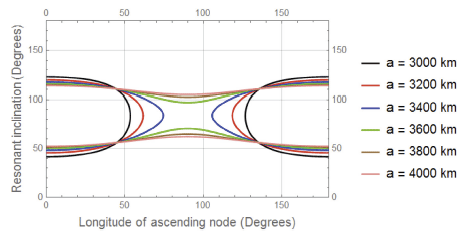
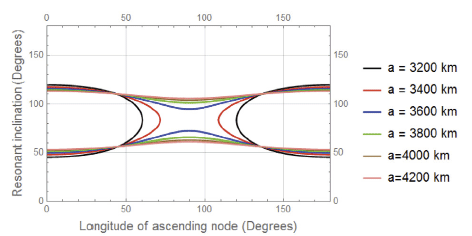
In this case we study the behaviour of the resonant inclination in degree in terms of changing the longitude of the ascending node.

8.3.1 Analysis of Figs. -

It is observed that all curves in Figs. 9–12 meet at two resonant inclinations, a relatively small perturbations in these inclinations are observed due to the change in the eccentricity from figure to figure. These results can be summerized in the following Table 3.

Fig. 9. The resonant inclination dynamics versus the the longitude of the ascending node, e = 0, ω = 45˚.

Download Original Figure

Fig. 10. The resonant inclination dynamics versus the the longitude of the ascending node, e = 0.1, ω = 45˚.

Download Original Figure

Fig. 11. The resonant inclination dynamics versus the the longitude of the ascending node, e = 0.15, ω = 45˚.

Download Original Figure

Fig. 12. The resonant inclination dynamics versus the the longitude of the ascending node, e = 0.2, ω = 45˚.

Download Original Figure

Table 3. Resonant inclinations versus argument of periapsis

Download Excel Table

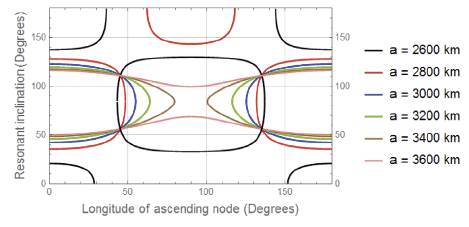
9. Conculsion

Due to the importance of the resonance dynamics, We have treated the problem of resonance caused by the some gravitational as well as nongravitational perturbations. The treated problem is of special interest due to many missions planned to Mercury, in past, present and in future. The important advantage of resonance study is to protect and preserve the orbits from the perturbations due to different gravitational forces. In order to make the problem tractable, we utilized some simplifying assumptions. The considered force model is constructed. Then the Deluanay canonical set is intorduced. We formulate the problem using the Hamiltonian framework, and orderd the Hamiltonian, then we used Lie transform to doubly average the problem.We compute the resonance capture. At the end of the work, we give some numerical simulations to capture the resonant inclinations, i.e. for eccentricity e = 0.2, and at Ω = 90˚, there are two resonant inclinations I = 46˚ and 120˚. Also, at ω = 45˚, there are two resonant inclinations I = 55˚ and 111˚ at different values for semi-major axis.

ACKNOWLEDGMENTS

The authors wish to introduce their profound thanks to reviewers and the editorial team due to their constructive criticism and fruitful discussions that helped improve the manuscript.

Notes

Elamira Hend Khattab https://orcid.org/0000-0001-5109-7410

Fawzy Ahmed Abd El-Salam https://orcid.org/0000-0002-4107-9347

Walid Rahoma https://orcid.org/0000-0002-3529-2731

References

Abd El-Salam FA, El-Tohamy IA, Ahmed MK, Rahoma WA, Rassem MA, Invariant relative orbits for satellite constellations: a second order theory, Appl. Math. Comput. 181, 6-20 (2006).

Abd El-Salam FA, Perturbative effects on a Mercurian orbiter due to the solar radiation pressure, solar wind and the coronal mass ejections, New Astron. 12, 490-496 (2007).

Anselmo L, Bertotti B, Farinella P, Milani A, Nobili AM, Orbital perturbations due to radiation pressure for a spacecraft of complex shape, Celest. Mech. 29, 27-43 (1983).

Arfken GB, Weber HJ, Harris FE, Mathematical Methods for Physicists: A Comprehensive Guide (Academic Press, Waltham, MA, 2012).

Breen AR, Riley P, Lazarus AJ, Canals A, Fallows RA, et al., The solar wind at solar maximum: comparisons of EISCAT IPS and in situ observations, Ann. Geophys., Eur. Geosci. Union. 20, 1291-1309 (2002).

Breiter S, Extended fundamental model of resonance, Celest. Mech. Dyn. Astron. 85, 209-218 (2003).

Breiter S, Lunisolar apsidal resonances at low satellite orbits, Celest. Mech. Dyn. Astron. 74, 253-274 (1999).

Breiter S, Lunisolar resonances revisited, Celest. Mech. Dyn. Astron. 81, 81-91 (2001b).

Breiter S, On the coupling of lunisolar resonances for Earth satellite orbits, Celest. Mech. Dyn. Astron. 80, 1-20 (2001a).

10.

Broucke RA, Long-term third-body effects via double averaging, J. Guid. Control Dyn. 26, 27-32 (2003).

11.

Carvalho JPS, Moraes RV, Prado AFBA, Nonsphericity of the moon and near sun-synchronous polar lunar orbits, Math. Probl. Eng. 2009, 740460 (2009a).

12.

Carvalho JPS, Moraes RV, Prado AFBA, Non-sphericity of the moon and critical inclination, Proceedings of the 32^nd Congresso Nacional de Matemática Aplicada e Computacional, Cuiab, Brazil, 10-20 Sep 2009b.

13.

Carvalho JPS, Moraes RV, Prado AFBA, Semi-analytic theory of a Moon artificial satellite considering lunar oblateness and perturbations due to a third-body in elliptic orbit, Proceedings of the 7^th Brazilian Conference on Dynamics, Control and Applications, Presidente Prudente, Brazil, 7-9 May 2008.

14.

Carvalho JPS, Moraes RV, Prado AFBA, Some orbital characteristics of lunar artificial satellites, Celest. Mech. Dyn. Astron. 108, 371-388 (2010).

15.

Celletti A, Analysis of resonances in the spin-orbit problem in celestial mechanics: the synchronous resonance (part I), Z. Angew. Math. Phys. 41, 174-204 (1990).

16.

Celletti A, Chierchia L, Hamiltonian stability of spin–orbit resonances in celestial mechanics, Celest. Mech. Dyn. Astron. 76, 229-240 (2000).

17.

Chametla RO, D’Angelo G, Reyes-Ruiz M, Javier Sánchez-Salcedo F, Capture and migration of Jupiter and Saturn in mean motion resonance in a gaseous protoplanetary disc, Mon. Notices Royal Astron. Soc. 492, 6007-6018 (2020).

18.

Cook GE, Luni-solar perturbations of the orbit of an Earth satellite, Geophys. J. Int. 6, 271-291 (1962).

19.

Costa Filho OO, Sessin W, The extended Delaunay method applied to first order resonance, Celest. Mech. Dyn. Astron. 74, 1-17 (1999).

20.

Deprit A, Canonical transformations depending on a small parameter, Celest. Mech. 1, 12-30 (1969).

21.

Domingos RC, Vilhena de Moraes R, Prado AFBA, Third-body perturbation in the case of elliptic orbits for the disturbing body, Math. Probl. Eng. 2008, 763654 (2008).

22.

Delhaise F, Morbidelli A, Luni-solar effects of geosynchronous orbits at the critical inclination, Celest. Mech. Dyn. Astron. 57, 155-173 (1993).

23.

El-Enna AA, Ahmed MKM, Abd El-Salam FA, Analytical treatment of the relativistic and solar radiation pressure effects on an artificial satellite, Appl. Math. Comput. 175, 1525-1542 (2006).

24.

El-Saftawy MI, Analytical study of the resonance caused by solar radiation pressure on a spacecraft, Astrophys. Space Sci. 295, 407-419 (2005).

25.

El-Saftawy MI, Ahmed MKM, Helali YE, The effect of direct solar radiation pressure on a spacecraft of complex shape, Astrophys. Space Sci. 259, 141-149 (1998).

26.

Elamira Hend Khattab et al. Resonance Capture for a Mercurian Orbiter in the Vicinity of Sun Ferrer S, Osácar C, Harrington’s Hamiltonian in the stellar problem of three bodies: reductions, relative equilibria and bifurcations. Celest. Mech. Dyn. Astron. 58, 245-275 (1994).

27.

Fitzpatrick PM, Principles of Celestial Mechanics (Academic Press, New York, NY, 1970).

28.

Folta D, Quinn D, Lunar frozen orbits, in AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, Co, 21-24 Aug 2006.

29.

Gilthorpe MS, Moore P, Winterbottom AN, Analysis of the orbital elements of the satellite COSMOS 1603 (1984-106A) at 14^th order resonance, Planet. Space Sci. 38, 1147-1159 (1990).

30.

Henrard J, Caranicolas ND, Motion near the 3/1 resonance of the planar elliptic restricted three body problem, Celest. Mech. Dyn. Astron. 47, 99-121 (1989).

31.

Kamel AA, Expansion formulae in canonical transformations depending on a small parameter, Celest. Mech. 1, 190-199 (1969).

32.

Khattab EH, Radwan M, Rahoma WA, Frozen orbits construction for a lunar solar sail, J. Astron. Space Sci. 37, 1-9 (2020).

33.

Kozai Y, Effects of solar radiation pressure on the motion of an artificial satellite, Smithsonian Contrib. Astrophys. 6, 109 (1963).

34.

Kwok JH, Doubly averaging method for third body perturbations, AAS Paper 91-464 (1991).

35.

Kwok JH, Long-term orbit prediction using an averaging method, AIAA Paper 84-1985 (1985).

36.

Lara M, Design of long-lifetime lunar orbits: a hybrid approach, Acta Astronaut. 69, 186-199 (2011).

37.

Lara M, Three-body dynamics around the smaller primary. Application to the design of science orbits, J. Aerosp. Eng. Sci. Appl. 2, 53-65 (2010).

38.

Lari G, Saillenfest M, Fenucci M, Long-term evolution of the Galilean satellites: the capture of Callisto into resonance, Astron. Astrophys. 639, A40 (2020).

39.

Lewis JS, Physics and Chemistry of the Solar System (Academic Press, Waltham, MA, 2004).

40.

Musen P, The influence of the solar radiation pressure on the motion of an artificial satellite, J. Geophys. Res. 65, 1391-1396 (1960).

41.

Prado AFBA, Third-body perturbation in orbits around natural satellites. J. Guid. Control Dyn. 26, 33-40 (2003).

42.

Pichierri G, Morbidelli A, Crida A, Capture into first-order resonances and long-term stability of pairs of equal-mass planets, Celest. Mech. Dyn. Astron. 130, 54 (2018).

43.

Rahoma W, Orbital elements evolution due to a perturbing body in an inclined elliptical orbit, J. Astron. Space Sci. 31, 199-204 (2014).

44.

Rahoma W, Abd El-Salam F, The effects of Moon's uneven mass distribution on the critical inclinations of a lunar orbiter, J. Astron. Space Sci. 31, 285-294 (2014).

45.

Rahoma WA, Khattab EH, Abd El-Salam FA, Relativistic and the first sectorial harmonics corrections in the critical inclination, Astrophys. Space Sci. 351, 113-117 (2014).

46.

Rickman H, Froeschle C, A keplerian method to estimate perturbations in the restricted three-body problem, Moon Planets. 28, 69-86 (1983).

47.

Roth EA, Construction of a consistent semianalytic theory of a planetary or moon orbiter perturbed by a third body, Celest. Mech. 28, 155-169 (1982).

48.

Scheeres DJ, Guman MD, Villac BF, Stability analysis of planetary satellite orbiters: application to the Europa orbiter, J. Guid. Control Dyn. 24, 778-787 (2001).

49.

Sehnal L, Non-gravitational forces in satellite dynamics, in Satellite Dynamics, eds. Giacaglia GEO, Stickland AC (Springer, Berlin, 1975).

50.

Sehnal L, Radiation pressure effects in the motion of artificial satellites, in Dynamics of Satellites (1969), ed. Morando B (Springer, Berlin, 1970), 262-272.

51.

Szebehely V, Perturbations of the regularized equations of the restricted problem of three bodies, Astron. J. 69, 309-315 (1964).