Analysis of Solar and Lunar Motions in the Seonmyeong Calendar

The inequality of the solar motion has been known as early as A.D. 570 in China (Needham 1959). In the Goryeosa, the apparent movements of the Sun considering its unequal motion are tabulated with respect to the solar term, as in the case of the Chongxiu-Daming calendar (refer to Choi et al. 2018a). A year was divided into 24 solar terms, as mentioned above, and two methods were utilized for determining the instants of the solar terms: mean and corrected (literal translation) methods. The former method is to equally divide the length of the tropical year into 24 intervals while the latter method is to equally divide the ecliptic into 24 intervals conceptually. Currently, the corrected method is utilized for determining the dates of 24 solar terms (KASI 2018). In both methods, the starting point is the instant of a winter solstice of the preceding year. With regard to calculating the daily movement of the Sun from each solar term, only the calculation procedure is explained in the Goryeosa. In the Japanese literature, meanwhile, the amounts of daily Sun movement in each solar term are tabulated.

We present the ready reckoner relating to the solar motion in Table 2, which is tabulated in the Goryeosa. In column 1 of the table, i represents the solar term notated with an Arabic number. For reference, i= 1, 7, 13, and 19 represent the winter solstice, spring equinox, summer solstice, and autumnal equinox, respectively. In column 2, ∆$U_S^G$ is the unequal amount of the solar motion in units of ${\text{min}}_{\text{H}}^{\text{G}}$ during the length of each solar term by the mean solar term method (i.e., Jungjeol) compared to its mean motion. In column 3, JG is the length of the ith solar term by the corrected solar term method given in units of d_H, ${\text{min}}_{\text{H}}^{\text{T}}$, and sec_H. Because the Sun moves faster and slower around the winter and summer solstices, respectively, than its mean motion, the values of JG could be obtained by subtracting or adding the value of $\Delta U_S^G$×100 to the Jungjeol (the units of $\Delta U_S^G$ is ${\text{min}}_{\text{H}}^{\text{G}}$ not ${\text{min}}_{\text{H}}^{\text{T}}$). As an example, the value of JG in the second solar term, JG₂, is 14 d_H 5235 ${\text{min}}_{\text{H}}^{\text{T}}$ 5 sec_H by subtracting +50×100 ${\text{min}}_{\text{H}}^{\text{T}}$ to the Jungjeol (i.e., 15 d_H 1835 ${\text{min}}_{\text{H}}^{\text{T}}$ 5 sec_H). In this sense, the value of 2335 ${\text{min}}_{\text{H}}^{\text{T}}$ for JG₁₈ in the Goryeosa is the typographical error of 2435 ${\text{min}}_{\text{H}}^{\text{T}}$, which is the same that for JG₇. In all tables, the values marked with the asterisk symbol are the corrected values in this study. In column 4, $U_S^G$ is the accumulation of $\Delta U_S^G$ until the preceding solar term; hence, the value of $U_S^G$ in the first term, $U_{S,1}^G$, is zero. In column 5, $\Delta U_S^M$ is the value dividing $\Delta U_S^G$×100 by the mean motion of the Moon per day, ${\overline{u}}_M^G$. Although the value of ${\overline{u}}_M^G$ is not defined, it was 13 d_A 31 ${\text{min}}_{\text{A}}^{\text{G}}$ (or 13.3689 d_A), according to our estimation in the next section. Adopting this value, we found that the values of $\Delta U_S^M$ were the results rounded half up. In addition, the value of $\Delta U_S^M$in the 14th solar term, $\Delta U_{S,14}^M$, should be +374 recorded as the value of the Tang dynasty in the Goryeosa. The last column, $U_S^M$, is the accumulation of the $\Delta U_S^M$ until the preceding solar term; hence, the value of $U_S^M$ in the first term, $U_{S,1}^M$, is zero. The value of $U_{S,17}^M$ is the typographical error in the Goryeosa. Although the Goryeosa states that the value of the Tang dynasty is 1246, it is recorded as 1346 in the version of the Xintangsh that we refer to in this study.

Table 2. Ready reckoner in relation to the solar motion.

Download Excel Table

As shown in Table 2, the solar motion is symmetrical around two solstices and equinoxes. The typographical errors discussed above can be verified from this perspective. In reality, however, the Earth revolves around the Sun and its motion is fast around the perihelion and slow around the aphelion. To estimate the accuracy of the solar motion in the SM calendar, we calculated the daily apparent movement of the Sun following the calculation procedures described in the Goryeosa. In Appendix A, we present the procedures using mathematical symbols and formulas to facilitate the understanding of contemporary concepts. As shown in the appendix, a quadratic equation was used to consider the inequality of the Sun, as in the Shoush calendar (refer to Choi et al. 2018b).

The length of the anomalistic month, 27 d_H 4658 ${\text{min}}_{\text{H}}^{\text{T}}$ (19 sec_H), was divided into two ranges referring to the apogee (A) and perigee (P). Hereinafter, Sectors I and II stand for the A-P and P-A ranges, respectively. To calculate the position of the Moon for a given time, the SM calendar used the daily apparent movement of the Moon in each sector, which was given in a tabular form. In Table 3, we present the table listed in the Goryeosa in relation to the lunar motion. In the table, column 1, denoted as m_A or m_P (integer), represents the day number since the instants of the apogee and perigee passages, respectively (hereinafter, m is the common designation for m_A and m_P). Because the day number was counted from the first day (i.e., m=1), the last day number in each sector was the 14th day. In column 2, $u_M^G$ is the apparent movement of the Moon in units of ${\text{min}}_{\text{A}}^{\text{G}}$ on its orbital during the day (i.e., 8400 ${\text{min}}_{\text{H}}^{\text{T}}$) on the mth day. In column 3, $\Delta u_M^G$ is the difference of two successive values in $u_M^G$ for m≤13, i.e., $\Delta u_M^G\left(m\right)=u_M^G\left(m+1\right)-u_M^G\left(m\right)$, and 0 for m = 14. In column 4, $u_M^D$ is the same quantity with $u_M^G$ but converted in units of d_A and ${\text{min}}_{\text{A}}^{\text{G}}$, which is listed in a separate table in the Goryeosa. For instance, because the value of $u_M^G$ on the third day in Sector II is 1203 ${\text{min}}_{\text{A}}^{\text{G}}$ (= 14×Gakbeob + 27 ${\text{min}}_{\text{A}}^{\text{G}}$), hence that of $u_M^D$ on the day is 14 d_A 27 ${\text{min}}_{\text{A}}^{\text{G}}$. Suppose that the ${\overline{u}}_M^G$ is the mean motion of the Moon per day and $\delta u_M^G$ is the difference between $u_M^G$ and ${\overline{u}}_M^G$. In columns 6 and 7, $\Delta u_M^M$ and $U_M^M$ are the physical quantities dividing $\delta u_M^G$ by ${\overline{u}}_M^G$ and accumulating $\Delta u_M^M$ until the preceding day, respectively; hence, $U_M^M$ is zero for m=1. Strictly speaking, the value of $\Delta u_M^M$ for the mth day, $\Delta u_M^M$ (m), is

Table 3. Ready reckoner in relation to the lunar motion.

Download Excel Table

where α is 1 except for m = 7 and 14. As shown in Table 3, two values are listed in $\Delta u_M^M$ for m = 7. These values can be obtained from Eq. (1) using the values of the Chosu and Malsuv on the 7th day. That is, two values in each sector can be obtained using α of 7465/8400 and 935/8400. Meanwhile, the value of $\Delta u_M^M$ for m = 14 is the result using the value of Chosu on the 14th day, i.e., α = 6529/8400. However, the value of the daily mean motion of the Moon is not stated in historical literature, as mentioned above. In addition, the daily apparent movement of the Moon in Sector I is not symmetrical to the movement in Sector II, as shown in column 1. Hence, a simple method of estimating the value of ${\overline{u}}_M^G$ is using the average of the minimum and maximum apparent movements of the Moon, i.e., 1012 and 1234 ${\text{min}}_{\text{A}}^{\text{G}}$, respectively. Subsequently, we can obtain the ${\overline{u}}_M^G$ of 1123 ${\text{min}}_{\text{A}}^{\text{G}}$ (= 13 d_A 31 ${\text{min}}_{\text{A}}^{\text{G}}$) or 13.1766 degrees. This value is similar to that defined in the Chongxiu-Daming calendar, i.e., 13.1763 degrees (Choi et al. 2018a) or as known in modern astronomy, i.e., 13.176358 degrees (Cox 2001). Applying the ${\overline{u}}_M^G$ value of 1123 ${\text{min}}_{\text{A}}^{\text{G}}$ to Eq. (1), we obtained a good agreement with the values of $\Delta u_M^M$ except for several cases indicating differences of approximately 1 ${\text{min}}_{\text{H}}^{\text{T}}$. In our opinion, the discrepancies might be caused by the significant figures in the mean motion of the Moon estimated in this study.

We estimated the accuracy of the solar and lunar motions by the SM calendar when the calendar was used in Korea by the Goryeo dynasty, and not in China by the Tang dynasty. Hence, we selected the periods of 919, 1155, and 1392 (i.e., the beginning, middle, and ending periods of the Goryeo dynasty, respectively) and compared the amounts of daily Sun and Moon movements listed in the Goryeosa with the results of modern calculations for each period. As mentioned earlier, the first step of the calendrical calculation in the SM calendar is to determine the instant of the CJDJ of a given year. However, in this study, we will not discuss the procedures of calculating the instant of the CJDJ in detail because they are well explained in the work of SADU (2016) where examples are provided. In principle, the instants of the CJDJ and those of the apogee passage are determined by accumulating the lengths of a tropical year and anomalistic month since the Super Epoch. However, it is noteworthy that the day of the winter solstice (also CJDJ) should be placed in the lunar November in Chinese calendars. In other words, a lunar November is the month containing the winter solstice day. In addition, it is noteworthy that the calendar days are obtained as a sexagenary circle instead of Arabic numbers. Hence, we referred to the work of Han (2001) to convert lunisolar days obtained as a sexagenery circle into Julian calendar days. Because the hour system of the SM calendar was based on the apparent solar time (AST), we also converted the AST at the Gaeseong (i.e., a capital of the Goryeo dynasty) into the mean solar time in Korean standard time (KST, i.e., at the meridian of 135° E) by correcting the longitudinal difference, equation of time (ET), and ∆T (i.e., time difference between the terrestrial time and universal time) (see also Lee et al. 2011). We assumed the longitude of the Gaeseong as 126° 33ʹ E, i.e., the longitudinal difference is -33.8 min (Lee 2017), and referred to the work of Morris and Stephenson (2004) for the value of ∆T (e.g., 34.5 min in 918). Finally, we used the astronomical algorithms of Meeus (1998) and the ephemeris of Standish et al. (1997) in modern calculations.

To estimate the accuracy of the solar motion, we first reproduced the instants of the CJDJ of the years used as the examples in the work of SADU (2016) and obtained the same results. Subsequently, we determined the instants of CJDJ of 919, 1155, and 1392 and summarized the results in Table 4 including the perihelion passage times in those days from modern calculations. In the table, YY, MM, DD, and HH represent the year, month, day, and hour, respectively. In the lunisolar date, the day is expressed with the notation utilized by Lee et al. (2012) and the unit of hour is ${\text{min}}_{\text{H}}^{\text{T}}$ as that in the AST. For instance, #55 November 1154 in the lunisolar calendar corresponds to 15 December 1154 in the Julian calendar, and 1905 ${\text{min}}_{\text{H}}^{\text{T}}$ in AST at the Gaeseong to 4.55 h in KST by correcting the longitudinal difference of -33.8 min, equation of time of -0.72 min, and ∆T of 14.7 min. According to our study, the difference between the CJDJ instant of 1155 and the perihelion passage time at that time was the smallest, i.e., -0.14 days, among the three periods. After determining the CJDJ instant, we computed the dates of the 24 solar terms by accumulating the Jungjeol and calculated the daily Sun movement by the SM calendar since the instant of each solar term throughout the procedures described in Appendix A. Subsequently, we compared the movements for 15 days in each solar term (i.e., for a total of 360 days) with the results of modern calculations. Hence, the interval between the last day in a solar term and the first day in the next solar term (i.e., next solar term day itself) is 1 d_H 1835 ${\text{min}}_{\text{H}}^{\text{T}}$ 5 sec_H, and not 8400 ${\text{min}}_{\text{H}}^{\text{T}}$ (i.e., a day).

Table 4. Summary of the CJDJ instants of 919, 1155, and 1392 by the SM calendar and the perihelion passage times in those days by modern calculations.

Download Excel Table

Figure 1 shows the differences in the daily apparent movement of the Sun between the SM calendar, S^SM, and modern calculations, S^MC, for the periods of 919, 1155, and 1392. The horizontal axis is the elapsed date since the CJDJ instant of each year and the vertical axis is $S_i^{SM}\left(n\right)-S_i^{MC}\left(n\right)$ in units of (modern) arcmin, where i is the solar term from 1 to 24 and n is the day number since each solar term from 0 to 14. In the figure, the red solid, green dot, and blue short-dash lines represent the results for the periods of 919, 1155, and 1392, respectively; the vertical dotted lines represent the elapsed dates of the spring equinox, summer solstice, and autumn equinox, from left to right, since the CJDJ instant of each year. For a quantitative comparison, we also estimated the MAD value defined as follows:

Fig. 1. Differences in daily solar motion between the SM calendar, S^SM, and modern calculations S^MC: red solid, green dot, and blue short-dash lines represent the results for the periods of 919, 1155, and 1392, respectively. The horizontal axis is the elapsed dates since the CJDJ instant of each year and the vertical axis is $S_i^{SM}\left(n\right)-S_i^{MC}\left(n\right)$ in units of (modern) arcmin. The vertical dotted lines are the elapsed dates of the spring equinox, summer solstice, and autumn equinox, from left to right, since the CJDJ instant of each year.

Download Original Figure

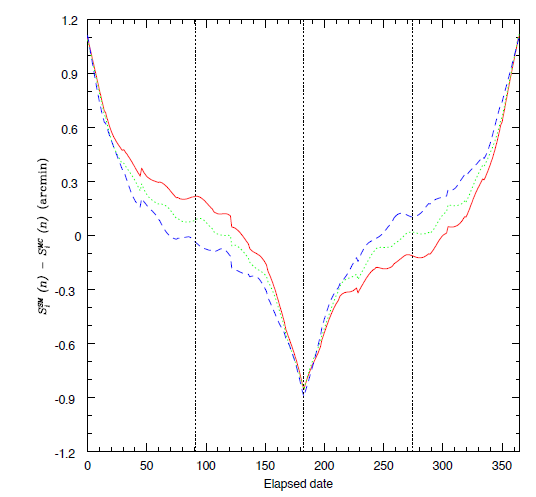
where X^SM and X^MC are physical quantities from the SM calendar and modern calculations, respectively, and N is the number of data used in the calculations. We found that the MAD values are 0.33, 0.30, and 0.31 arcmin for the periods of 919, 1155, and 1392, respectively. In addition, the pattern in Figure 2 is similar to that in the result of the Chongxiu-Daming calendar of the Jin dynasty for the solar motion: the maximum differences are indicated around the winter and summer solstices, and the minimum around the spring and autumn equinoxes (refer to Choi et al. 2018a).

Fig. 2. Differences in daily lunar motion between the SM calendar, M^SM, and modern calculations, M^MC: red solid, green dot, and blue short-dash lines represent the results for the periods of 919, 1155, and 1392, respectively. The horizontal axis is the day number since the instant of the apogee passage and the vertical axis is M^SM (m)-M^MC (m) in units of (modern) degrees, which are averaged over the 12 cycles of anomalistic month length for each day number.

Download Original Figure

In the lunar motion section of the Goryeosa, the methods of determining the elapsed dates of four phases of the Moon (i.e., new, first quarter, full, and last quarter moons) since the instant of an apogee passage are described. In addition, the instant of the apogee passage to calculate the elapsed date of the new moon in lunar November was computed using the length of the Yeonyeo (i.e., the difference in instants between the CJDJ and apogee passage around that time). For this study, however, we obtained the instant of the apogee passage immediately before the CJDJ instant (hereinafter, the CJAP instant) by accumulating the length of the anomalistic month from the Super Epoch. In Table 5, we present the instants of the CJAP referring to the instants of the CJDJ of 919, 1155, and 1392 together with the results of modern calculations.

Table 5. Summary of the instants of CJAP of 919, 1155, and 1392 by the SM calendar and the differences with apogee passage times in those days by modern calculations.

Download Excel Table

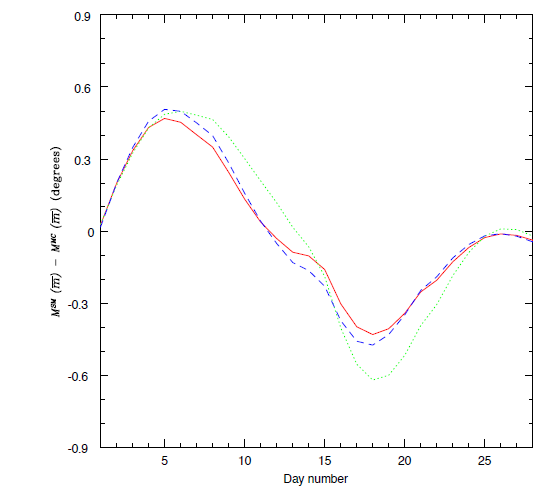
To estimate the accuracy of the lunar motion in approximately one tropical year, we first determined 12 successive instants of the apogee passage in each year by accumulating the anomalistic month length to the CJAP instant. Subsequently, we calculated the daily Moon movement during each anomalistic month length using the DE405 ephemeris. As indicated in Section 3.2, however, the lunar movement listed in Table 3, $u_M^G$, is the daily amount (i.e., for 8400 ${\text{min}}_{\text{H}}^{\text{T}}$) for 28 days since the instant of an apogee passage although the length of the anomalistic month is 27 d_H 4658 ${\text{min}}_{\text{H}}^{\text{T}}$ 19 sec_H. Therefore, in modern calculations for the daily lunar movement, we determined the beginning point of each day by accumulating 8400 ${\text{min}}_{\text{H}}^{\text{T}}$ from the instant of an apogee passage but reset the point on the days of m_A= 8 and m_P= 1 and 8 using the Chosu of the 7th and 14th days. For example, the beginning point on m_A= 8 is 7 d_H 7465 ${\text{min}}_{\text{H}}^{\text{T}}$ and not 8 d_H 0 ${\text{min}}_{\text{H}}^{\text{T}}$ if the instant of each apogee passage is 1 d_H 0 ${\text{min}}_{\text{H}}^{\text{T}}$. From the comparison with the movements listed in the Goryeosa, we found that the MAD values are 0.217, 0.284, and 0.240 (modern) degrees for the periods of 919, 1155, and 1392, respectively. In Figure 2, we present the differences in daily Moon movement between the SM calendar, M^SM, and modern calculations, M^MC. The horizontal axis is the day number since the instant of an apogee passage, and the vertical axis is $M^{SM}\left(\overline{m}\right)-M^{MC}\left(\overline{m}\right)$ in units of (modern) degrees, which are averaged over the 12 cycles of anomalistic month length for each day number. In the figure, the legend is the same as that in Figure 1: red solid, green dot, and blue short-dash lines represent the results for the daily Moon movement for the periods of 919, 1155, and 1392, respectively.

According to the work of Qu (2008), the method of calculating the daily Sun movement was based on the Dayan calendar of the Tang dynasty. In the following, we formulated the calculation procedures explained in the Goryeosa. First, calculate the physical quantities of the Jungryul (JR), Hapcha (HC), and Jungcha (JC):

where i represents the ith solar term; $\Delta U_{S,i}^G$ and JG_i are physical quantities in the ith solar term, which are given in Table 2, and α is the Gakbeob (i.e., 84). In addition, the value of JR_i+1 in Eq. (A.2) should be substituted as JR_i-1 in the calculations of HC_i for i = 6, 8, 12, and 18 (i.e., solar terms incurring the sign change in the value of $\Delta U_S^G$ compared to each subsequent solar term). Subsequently, compute the following quantities: Ilcha (IC), Choryul (CR), Malryul (MR), Chojeongryul (CJR), and Maljeongryul (MJR).

where β is 100. In the SM calendar, the addition or subtraction operation differs with respect to the solar term in calculating the values of CR_i, MR_i, CJR_i, and MJR_i. However, these values can be obtained from Eqs. (A.5) and (A.6) if adopting the signing system given in Table 2. Finally, the daily inequality of the Sun (or equation of center of the Sun) in the ith solar term is obtained by cumulatively subtracting IC_i from CJR_i. That is, the unequal amount of the solar motion on the nth day in the ith solar term, $\Delta U_{S,i}^G$ (n), is

where n is the day number (integer) from 0 (i.e., day of each solar term) to 15, and γ is the decimal fraction when converting the length of the Jungjeol into units of d_H (i.e., $\frac{1835+5/8}{8400}$ ).

According to our examination, however, the values of α and β should be a unity (see also Martzloff 2016). This can be verified by summing $\Delta U_{S,i}^G(n)$ for n from 0 to 15. That is, the value of ${\displaystyle \sum }_{n=0}^{n=15}\Delta U_{S,i}^G(n)$ for a given solar term should equal to that of $\Delta U_{S,i}^G$ In addition, we reproduced the amounts of $\Delta U_S^M$ on the nth day in the ith solar term, $\Delta U_{S,i}^M\left(n\right)$, using the same method to obtain $\Delta U_{S,i}^G(n)$. Except for $\Delta U_{S,2}^M(n)$, in which their errors were already discussed by Soma (2014), we found an exact agreement with the values listed in the Seonmyoreki, a Japanese SM calendar preserved in the National Library of Korea, and the Sanpo. Finally, the unequal amount of solar motion until the nth day in the ith solar term, $U_{S,i}^G(n)$, is calculated as follows:

It can be rewritten as

This equation indicates that a quadratic equation was utilized to consider the inequality of the Sun.