1 INTRODUCTION
As satellite formation flying technology has advanced, it has become possible to perform several space missions that could not be performed with a single satellite. In the Gravity Recovery and Climate Experiment (GRACE) mission, two satellites flying in formation gathered data for the Earth gravitational model (Kroes et al. 2005). TerraSAR-X and TanDEM-X were flying in formation to generate the global digital elevation model (DEM) using synthetic aperture radar (SAR) (Krieger et al. 2007). PRISMA mission also navigated using relative positions based on global positioning system (GPS) (Candela et al. 2016). By using precise relative navigation, collision avoidance could also be maintained (Hwang et al. 2013). Precise relative navigation is required to succeed in these various formation flying missions. Various studies such as a satellite relative dynamic model (Park et al. 2009) have been conducted to provide precise relative navigation. In particular, the means to provide observations to improve relative navigation have been studied. The relative navigation algorithms are modified from the algorithms of absolute satellite navigation (Shin et al. 2016;Kim et al. 2017;Lee et al. 2017a, b). Fundamentally, relative navigation can be performed using GPS signals (Montenbruck et al. 2002). Park et al. (2008) and Sim et al. (2009) presented relative navigation algorithms based on the extended Kalman filter (EKF) and unscented Kalman filter (UKF) using GPS measurements. The relative navigation performance can be improved by using measurements other than GPS data. Recently, relative navigation algorithms using a miniaturized femtosecond laser distance meter have been developed. Jung et al. (2012) introduced a relative navigation algorithm based on laser measurements and laser pointing vectors. Lee et al. (2015) introduced a laser-based relative navigation algorithm using GPS measurements. It showed better performance than an algorithm using only GPS measurements. Furthermore, it was more precise than the algorithm using only laser measurements when the error of the angle data was large. Oh et al. (2016) improved carrier-phase differential GPS (CDGPS) by applying the laser measurements to GPS integer ambiguity estimation. The relative navigation algorithm by Oh et al. (2016) had not been compared with the other methods. The algorithms were verified using theoretically simulated laser measurement data that did not consider the hardware properties of the instrument. Lee et al. (2018) presented relative navigation using intermittent laser-based measurement data.
In this study, the performance of the previous algorithms (Jung et al. 2012;Lee et al. 2015;Oh et al. 2016) is compared under various conditions and with improved laser measurement data that includes the hardware properties of the instrument. Numerical simulations are conducted on hardware-in-the-loop simulator (HILS) developed by Park et al. (2010). Each navigation method has different characteristics, which are reflected in the simulation results. By utilizing the results of this study, a satellite relative navigation strategy could be figured out according to the space operating environments. Based on the simulation results, we selected the algorithm with the highest performance among the three, according to the operating environment and identified the points where the performance-rank changed. Based on pre-determined points, a strategy was developed to have the best performance among the navigation algorithms loaded on the satellites, by switching to an appropriate algorithm whenever the environment changed. First, coordinate systems and the algorithms used in this research are explained briefly. Then, the simulation results are analyzed. Finally, a relative navigation strategy is presented based on the simulation results.
2 COORDINATE SYSTEM
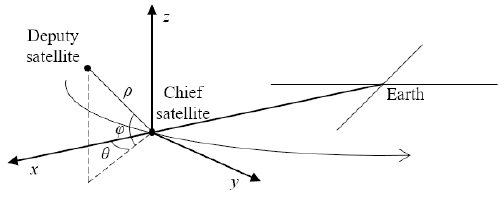
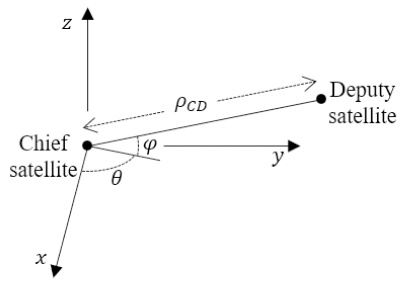
In this research several coordinate systems were used. The absolute orbit of satellites was determined in Earth-centered, Earth-fixed (ECEF) coordinates using GPS data. The determined orbit was transformed to Earth-centered inertial (ECI) coordinates to be utilized for relative orbit determination. Fig. 1 shows the relative coordinate systems used to describe a relative position of a deputy satellite in relation to the chief satellite. The relative orbit of the deputy satellite is determined in RSW coordinates and spherical coordinates. The center of RSW coordinates is the center-of-mass of the chief satellite. The radial direction of the chief satellite from Earth is set to an x-axis. A normal direction of the chief satellite’s orbit is set to a z-axis. A velocity direction of the chief satellite perpendicular to the x-axis and z-axis is set to a y-axis. In spherical coordinates, parameter ρ means the intersatellite distance (between the chief and the deputy). Parameters θ and φ mean angular displacement from the x-axis on the x-y plane and from the x-y plane to the z-axis, respectively.
3 RELATIVE NAVIGATION ALGORITHMS
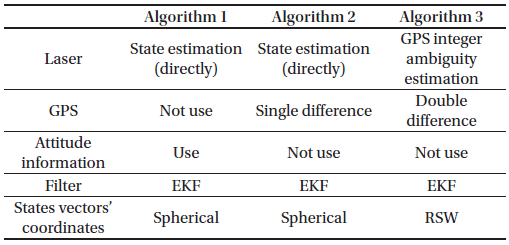
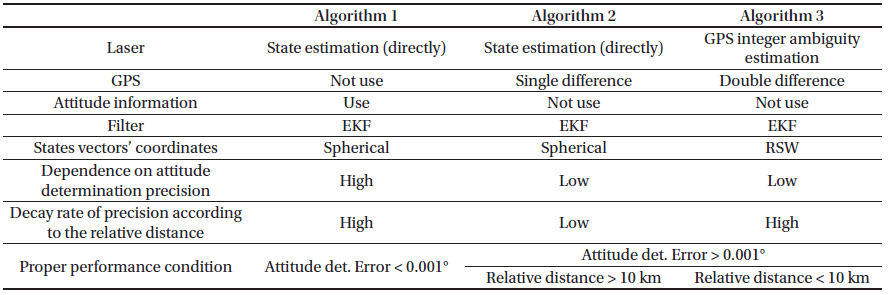
In this research, the performance of three algorithms was compared. Table 1 shows the technical characteristics of the algorithms. Algorithm 1 uses only laser measurements to determine the position of the deputy satellite. Algorithm 2 and 3 use both laser measurements and differences of GPS measurements. Algorithm 1 and 2 estimate the position of the deputy satellite in spherical coordinates, which are then converted to RSW coordinates. Because of the conversion, the error of the angles has a large effect on positioning error when the distance between the satellites is far. On the other hand, Algorithm 3 directly estimates the position in RSW coordinates. The algorithms determine the relative orbit in real time using EKF. In this paper, the explanation of the EKF procedure is omitted because it is a well-known method.
The relative orbit of the deputy can be determined using laser ranging data and the direction angle of the laser (Jung et al. 2012). Eq. (1) is the state vector. Position and velocity in spherical coordinates are estimated (see Fig. 2). Below, ρCD & indicate the inter-satellite range and range rate between the chief satellite and the deputy satellite.
Eq. (2) indicates the measurement data, which consists of range data L measured by laser, and laser pointing angle . The pointing vector is estimated based on attitude information.
Eq. (3) is the measurement model used in EKF. The H matrix, a Jacobian matrix of the measurement data, was derived from Eq. (3).(4)
The laser measurement data L shows drift due to the range rate (Jung et al. 2012). The scale factor of the drift is κ. The error levels of the measurement data were determined by laser distance meter specification and attitude-determination error. The estimation result in spherical coordinates is directly related to the measurement error. In particular, large attitude determination errors make the performance of relative navigation worse because the inter-satellite range increases.
The relative orbit of the deputy satellite with respect to the chief satellite can be determined by using laser ranging data and GPS data (Lee et al. 2015). Algorithm 1 is affected by the attitude determination precision. To compensate for this defect, Algorithm 2 utilizes the single difference of the GPS pseudo-range data instead of the attitude information. The pseudo-range includes errors caused by clock bias, ionospheric path delay, and some other terms. The ionospheric path delay and the GPS satellite’s clock offset terms can be neglected by subtracting the pseudo-ranges of the chief and the deputy satellites (Montenbruck et al. 2002). Eq. (5) is the state vector estimated by Algorithm 2. The last element δtCD is the difference between the GPS clock bias in the chief and the deputy satellites.
Eq. (6) indicates the measurement data.
This data consists of laser measurement data L and differences between the pseudo-range data of the chief and the deputy satellites from the jth GPS satellite . Eq. (7) is a measurement model.
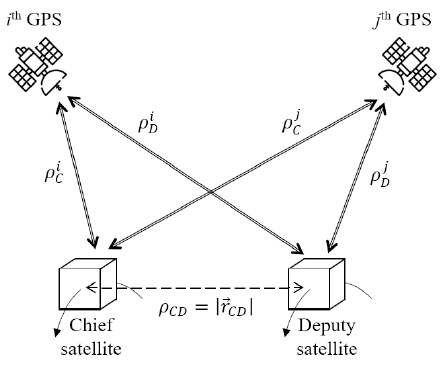
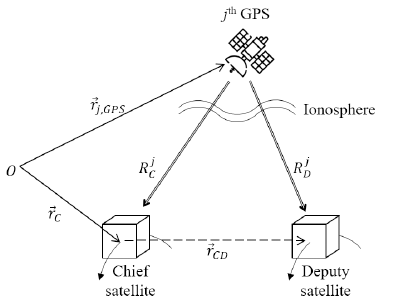
Here, means the position vector of the chief satellite, c is the speed of light, and means the relative position vector of the deputy satellite from the chief satellite. The term means the position vector of the jth observable GPS satellite (see Fig. 3).
Eq. (8) is the H matrix derived from Eq. (7).
The relative position of the chief to the GPS satellites is omitted because it is irrelevant to the relative orbit of the deputy satellite. The pseudo-range data is smoothed using the carrier phase data.
The carrier-phase differential GPS (CDGPS) can be improved with laser measurement data (Oh et al. 2016). In CDGPS, the double difference of the pseudo-range and carrier-phase are used. It is essential to determine the GPS integer ambiguity accurately to utilize the carrier-phase measurements. In other words, a representative cause of error of CDGPS is failure to estimate GPS integer ambiguity. By supplementing the laser measurement data at the sub-millimeter level, the success rate of the integer ambiguity determination increased. As a result, it improved the performance of the CDGPS. The state vector includes variations of the position and the velocity of the chief satellite, as well as the relative position and the relative velocity of the deputy satellite because this algorithm uses the linearized GPS measurement model. It also includes integer ambiguity (see Eq. 9).
In Eq. (9), means the integer ambiguity of the carrier-phase from the jth GPS satellite to the chief satellite and , element of the state vector, is the double difference of the integer ambiguities. Three kinds of measurement data were used. The double difference pseudo-range data were modeled as follows:
where is the relative distance between the chief satellite and jth GPS satellite (see Fig. 4), is the unit vector of difference between the pseudo-range data of the deputy satellite from ith and jth GPS satellites.
Similarly, the double difference carrier phase data was modeled as follows:(11)
where λ denotes wavelength. The laser measurement data was modeled as follows:(12)
The left sides of Eq. (10–12) involve the measurement data of the EKF. The right sides are the measurement model that the H matrix is derived from.
The laser measurement terms are represented in the last row of the H matrix, which plays an important role in the laser-based baseline measurements. It increases the resolution success rate of the integer ambiguity. In particular, the laser measurements are more effective when the inter-satellite range is too far to resolve the integer ambiguity using only the GPS measurements (Oh et al. 2016).
4 RELATIVE NAVIGATION SIMULATION
The laser measurement data was generated by a laser simulation algorithm introduced in Jung et al. (2012). The laser measurement data additionally considers the hardware properties caused by electrical circuits and RF elements in the instrument (Kang et al. 2017). The generated laser measurement data has about 100 μm level error within 10 km and worse performance as the inter-satellite range increases.
The GPS signal is generated by a Spirent GSS6560 GNSS simulator, which uses the true state data of the chief and the deputy satellite to produce the GPS L1 signal observed by the receiver (AsteRX1 PRO) manufactured by Septentrio Inc. The GNSS simulator and the receiver are components of the HILS. They make a GPS signal reflecting the hardware properties in real time (Park et al. 2010). The true state data of the chief and the deputy satellites are simulated by numerical integration of the dynamic model, which includes acceleration due to gravitational forces (Earth, Moon, and Sun), atmospheric forces, and solar radiation pressure. In contrast, the dynamic model in the EKF only considers the J2 term as perturbation to reduce the computational burden.
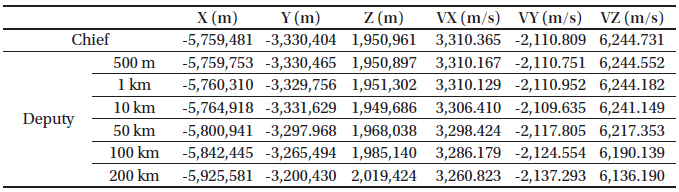
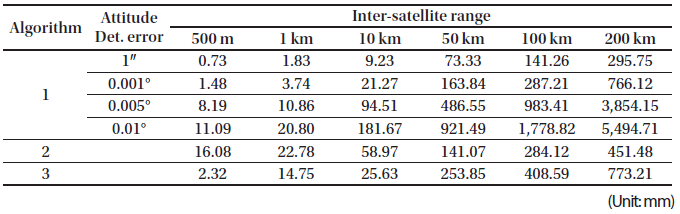
To analyze the performance of each algorithm, we compared the accuracy of the simulation results of the relative distance between the satellites and the attitude determination accuracy. For the initial conditions of the chief and deputy satellites, the relative distance was set from 500 m to 200 km on a projected circular orbit (PCO). The attitude determination accuracy was set to 1″, 0.001°, 0.005°, and 0.01°. The components of the position and velocity in the ECEF frame for each of the chief and the deputy satellites are presented in Table 2. The simulations ran for 5,000 seconds and the sampling time of the GPS and laser measurement data was one second.
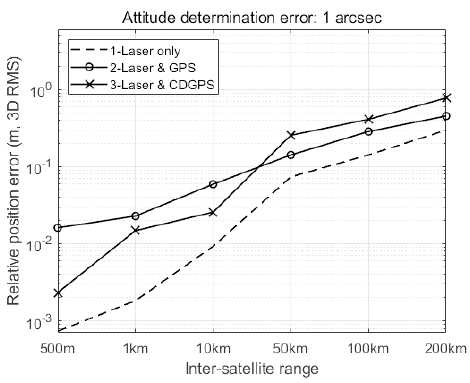
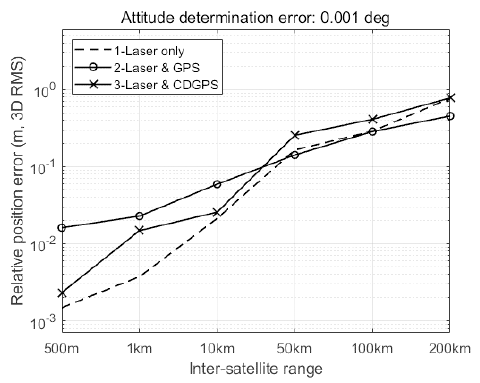
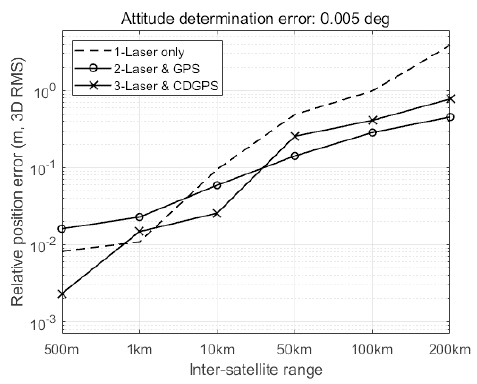
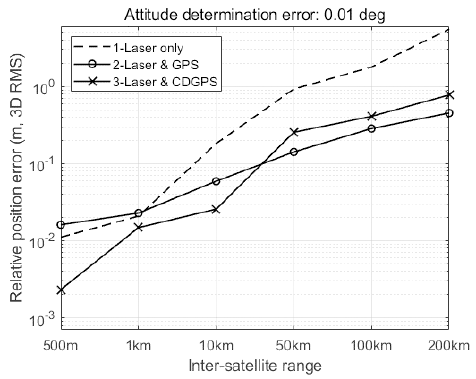
Table 3 shows the simulation results, which represent the 3D root-mean-square (3D RMS) of the relative position determination error in millimeters. The performance of Algorithm 1 deteriorates in proportion to the attitude determination error. The performances of Algorithm 2 and 3 are unrelated to the satellite attitude. As the relative distance increases, the precision decay rate of Algorithm 3 is faster than that of Algorithm 2. Algorithm 1 has a rate similar to that of Algorithm 3. When the inter-satellite range is less than 10 km, Algorithm 3 has better performance than Algorithm 2. In contrast, Algorithm 2 is more precise than Algorithm 3 when the relative distance is greater than 10 km. Figs. 5–8 show the comparison results of Algorithm 1 with the other algorithms. Algorithm 1 had the best performance when the attitude determination error was 1″ (see Fig. 5). When the deputy was closer than 10 km, the relative navigation error of Algorithm 1 was smaller than the error of the others with 0.001° attitude determination error (see Fig. 6). Figs. 7 and 8 show that Algorithm 1 is similar or worse. Consequently, the relative navigation was conducted using Algorithm 1 when the attitude determination was precise. In the other cases, an appropriate algorithm should be selected (see Table 4).
|
|
5 CONCLUSIONS
In this research, real-time relative navigation algorithms using the laser and GPS measurement data were assessed. Software simulation was conducted to compare the performance of the algorithms using various inter-satellite range and precision of attitude determination. For numerical evaluation, the simulation results were represented as 3D RMS error. If the high-precision attitude determination system is guaranteed, the algorithm that uses only the laser measurements can have the best navigation result. Performance degradation, however, stands out as the attitude determination precision worsens. The same performance were maintained regardless of the attitude determination error, when the laser and GPS measurements were combined. Therefore, if the deterioration of attitude determination occurs, perhaps due to such as malfunction of the attitude sensors, it would be more strategic to choose combined laser-GPS or combined laser-CDGPS relative navigation. Within about 10 km inter-satellite range, the laser-CDGPS combined relative navigation should be conducted because its error is smaller than the other’s. Although the switching point of the algorithms using combined measurements is determined at around 10 km inter-satellite range, the practical point should be determined in detail by considering several conditions, such as the characteristics of the satellite system or the mission environment. In conclusion, a reasonable relative navigation algorithm can be chosen for suitable performance based on the simulation results.