1. INTRODUCTION
Frozen orbits are characterized by nearly constant orbital eccentricity (e) and periapsis argument (ω), as discussed by Parke et al. (1987). These orbits are achieved through careful minimization of the drift rates associated with these orbital elements, resulting in an invariant geometric configuration and fixed spatial locations. Consequently, the line of apsides remains a constant vector in the geocentric frame of reference. Examples of commonly used frozen orbits for remote sensing and communication purposes include GEOSAT, LANDSAT, and Molniya.
Tzirti et al. (2009), Carvalho et al. (2010) and Khattab et al. (2020) have conducted analyses on frozen lunar artificial satellites, considering various perturbing models. Tzirti et al. (2010), along with Lara et al. (2010a, b), have explored frozen orbits around Mercury using Lie-Deprit transforms. Delsate et al. (2010), employing a Hamiltonian formalism, determined stable and unstable Mercurian frozen orbits locations. Liu et al. (2010, 2011) have investigated Martian frozen orbits and critical inclination orbits. Rahoma et al. (2014) addressed the critical inclination problem within the Hamiltonian framework, incorporating relativistic corrections and the first sectorial harmonics for an Earth-like planet. Additionally, Rahoma & Abd El-Salam (2014) examined the impact of oblateness and the first sectorial and tesseral harmonics coefficients on a lunar artificial satellite’s critical inclination.
Frozen orbits topic related to uncharged satellites has been extensively studied, Lanchares et al. (2011) conducted an analytical examination of frozen orbit families concerning a prolate celestial body. Abd El-Salam & Abd El-Bar (2016) and Abd El-Salam et al. (2018) investigated specific frozen orbit families for lunar artificial satellites using a singly averaged Hamiltonian considering the oblate and triaxial Moon. Masoud et al. (2018) studied the artificial frozen orbit problem around Earth. Ultimately, the application of frozen orbit concepts may be employed in the orbital design for specific missions within the context of the three-body problem, as highlighted by Zotos (2015).
The prolem’s history extended to include orbits undergoing resonant capture, as demonstrated by Quinn et al. (1995), and Haberman et al. (1999) and the influences of zonal harmonic, sectorial harmonic, and the Earth acting as a third-body perturber, Nie & Gurfil (2018).
Oliveira et al. (2019) investigated the perturbing effects of the Sun on the orbital evolution of artificial satellites following frozen orbits around Mars. A mapping of an irregular asteroid, 216 Kleopatra, research was carried out by Circi et al. (2019), who looked at ground track characteristics related to a frozen orbit.
A frozen orbit maintenance technique for small body exploration was presented by Li et al. (2019). The viability of station-keeping for spacecraft in near-polar and extremely low-altitude quasi-frozen orbits around the Moon was discussed by Singh et al. (2020).
Moreover, the electromagnetic (EM) force, accelerating the charged particle moving in relation to the geomagnetic field, acts perpendicular to its velocity and the magnetic field referred as Lorentz force, see Streetman & Peck (2007a, b) for comprehensive studies. The perturbation induced by EM forces on a charged satellite encompasses several noteworthy properties that significantly influence its orbital dynamics. Firstly, the strength of the EM force acting on the satellite is directly proportional to the product of its charge and the strength of the magnetic or electric field in its vicinity. This implies that a higher charge or a more intense EM field will result in a more pronounced perturbation. Additionally, the direction of the force depends on the relative orientation of the satellite’s charge and the magnetic or electric field vector, contributing to alterations in its trajectory. The perturbation is also influenced by the satellite’s velocity, with greater velocities leading to increased effects due to the interaction between the charged satellite and the surrounding EM fields. Managing and mitigating these perturbations is crucial for accurate satellite positioning and navigation in space missions, highlighting the importance of understanding the intricate properties of EM force-induced perturbations.
The dynamics of electrically charged satellites have been addressed employing Lagrange’s planetary equations by several authors, as Sehnal (1969), Peck (2005), Abdel‐Aziz (2007), Atchison & Peck (2009), Streetman & Peck (2009), Abdel-Aziz & Khalil (2014), Li (2016), Abd El-Salam et al. (2017), Abd El-Bar & Abd El-Salam (2018), Tealib et al. (2020). Using Lie series based on Kamel technique, Kamel (1970), the problem is treated differently and canonically.
This study concerns with the charged satellite’s frozen orbits computations. Our approach considers the oblate geopotential up j6 zonal harmonics enhanced by the first tesseral harmonics.
After this introduction, the single average Hamiltonian is presented in section 2 whereas, the frozen line of apses is addressed in section 3. In section 4, and its subsections, different investigated orbits of the solution of the equation frozen line of apses for the inclination as a freezing parameter for different cases are simulated and discussed. In section 5, the frozen apsidal line equation is solved for the argument of periapsis. In section 6, and its subsections, plotting and analysis are done on several examined orbits of the frozen line of apses solution for the periapsis argument freezing parameter for various circumstances. The freezing eccentricity is calculated in section 7. Section 8 presents the solution to the inclination frozen equation. Three-dimensional graphical representations of the frozen eccentricity are displayed in section 9. The phase space of the eccentricity vector is covered in section 10. Plots of the eccentricity vector’s 2D and 3D phase space portraits are shown in section 11. Section 12 concludes with some last thoughts and recommendations for further research.
2. SINGLY AVERAGED HAMILTONIAN
Recall the six orbital elements (a, e, I, ω, Ω, f), namely the semimajor axis, the eccentricity, the inclination, the argument of periapsis, the longitude of the ascending node and the true anomaly respectively, and the satellite’s longitude of the ascending node (ω⊕) occurs inextricably linked the Earth’s celestial longitude in the frame rotating with the Earth, then the Delaunay variables (l, g, h, L, G, H) can be read as; Delhaise & Morbidelli (1993) and Rahoma (2014, 2016):
where M is referes to mean anomaly and t refers to the time.
Employing the normalization perturbed Keplerian systems technique by Ahmed (1994), to define the singly averaged Hamiltonian pertaining to the dynamics of a charged satellite in the gravitational field considering the oblateness zonal harmonics up J6 and the first tesseral harmonic in the geopotential as :
where the following definitions have been made , C = cosI = H / G, S = sinI, λ2,2 is the corresponding reference longitude along the equator corresponding to J22 tesseral harmonics, and As, and the dimensionless parameters of the problem are defined by
where q is the net charge carried by the satellite, is the Schmitt coefficients, qdip is the dipole charge, d is the distance between its poles, and ε0 is the permittivity of free space, m is the mass of the charged body, with the following numerical parameters (Table 1).
3. THE APSES’ FROZEN LINE
The periapsis will be enforced to freeze at,
Using the binomial theorem with either a fractional exponents or with negative integers, Eq. (4) retaining orders up to C6 can be written, after some tedious algebraic calculations, as an algebraic equation of degree six in C = cos I as
that can be rewritten as
where
Disregarding the harmonics greater than the first order and EM perturbations, the quartic equation can be simplified into a quadratic form using coefficients,
Since A1,2η3,4 ≠ 0, the solution of this equation introduces the classical critical inclination as defined in the theory of artificial satellites.
4. DIFFERENT INVESTIGATED ORBITS OF EQ. (4)
In what follows we are going to study three case studies, in each case study we will study three subcases.
In the first case we will investigate the freezing inclination versus the argument of periapsis for three subcases; namely Low, Medium, and High Earth Orbits.
Fig. 1 simulate the impact of the frozen inclination (in degrees) concerning the argument of periapsis for satellites at Low Earth Orbits. These simulations are considered the gravitational effects (GE) influence alone and combined with EM effects, respectively.
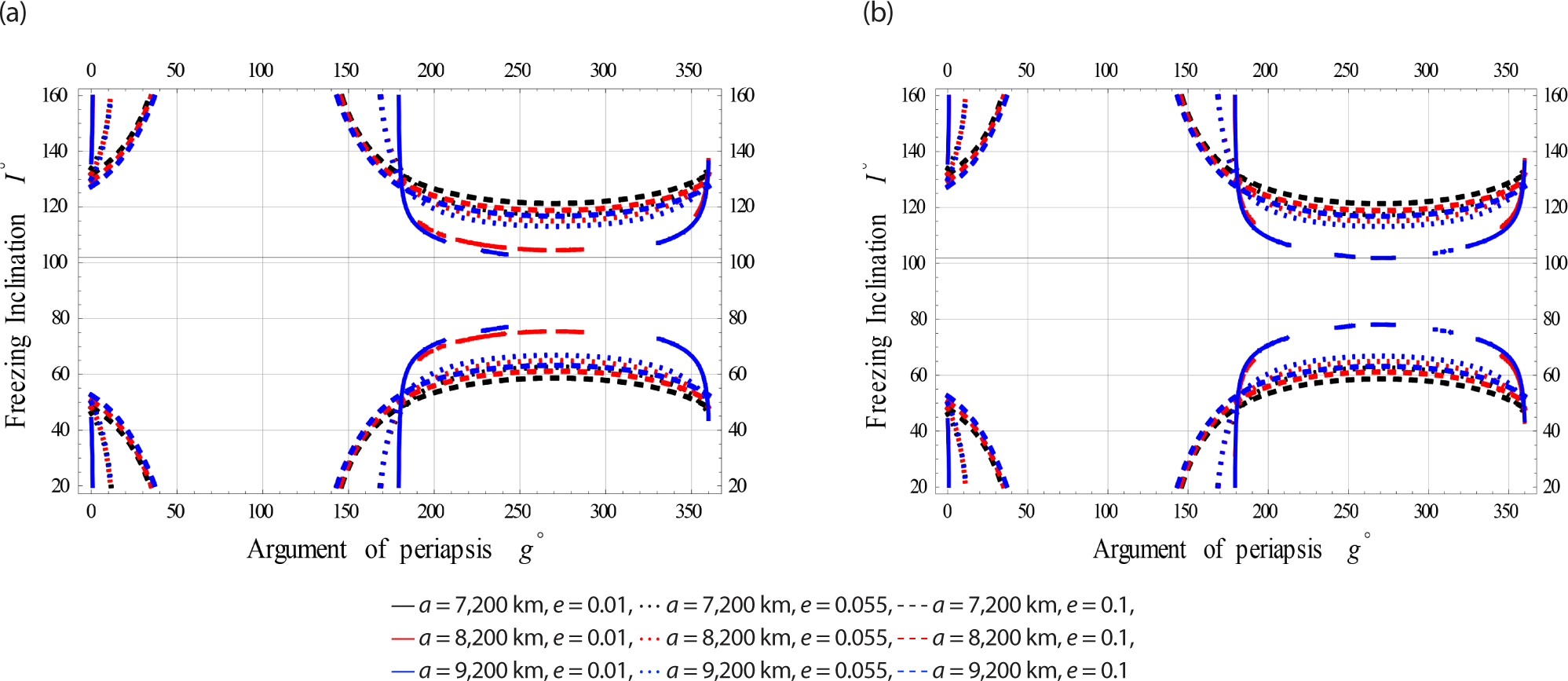
The figures reveal that the freezing inclination could be obtained for the whole range of the argument of perapsis.
The same procedure is repeated but for Meduim Earth Orbits in Fig. 2.
Also, the procedure ir repeated for High Earth Orbits in Fig. 3.
The color indicator of these Figs. are attached as legends next to each Fig. From all these Figs. the effect of EM field on the freezing inclination of a charged satellite in visible with different sizes of perturbations. In all these figures the obtained bands of freezing inclinations are dependent on the satellite’s altitude, as well as the orbiy’s eccentricity.
In this second secton. we will study the freezing inclination versus the semi-major axis for three subcases; namely Low, Medium, and High eccentricity Orbits considering (GE) influence alone and combined with EM effects, respectively.
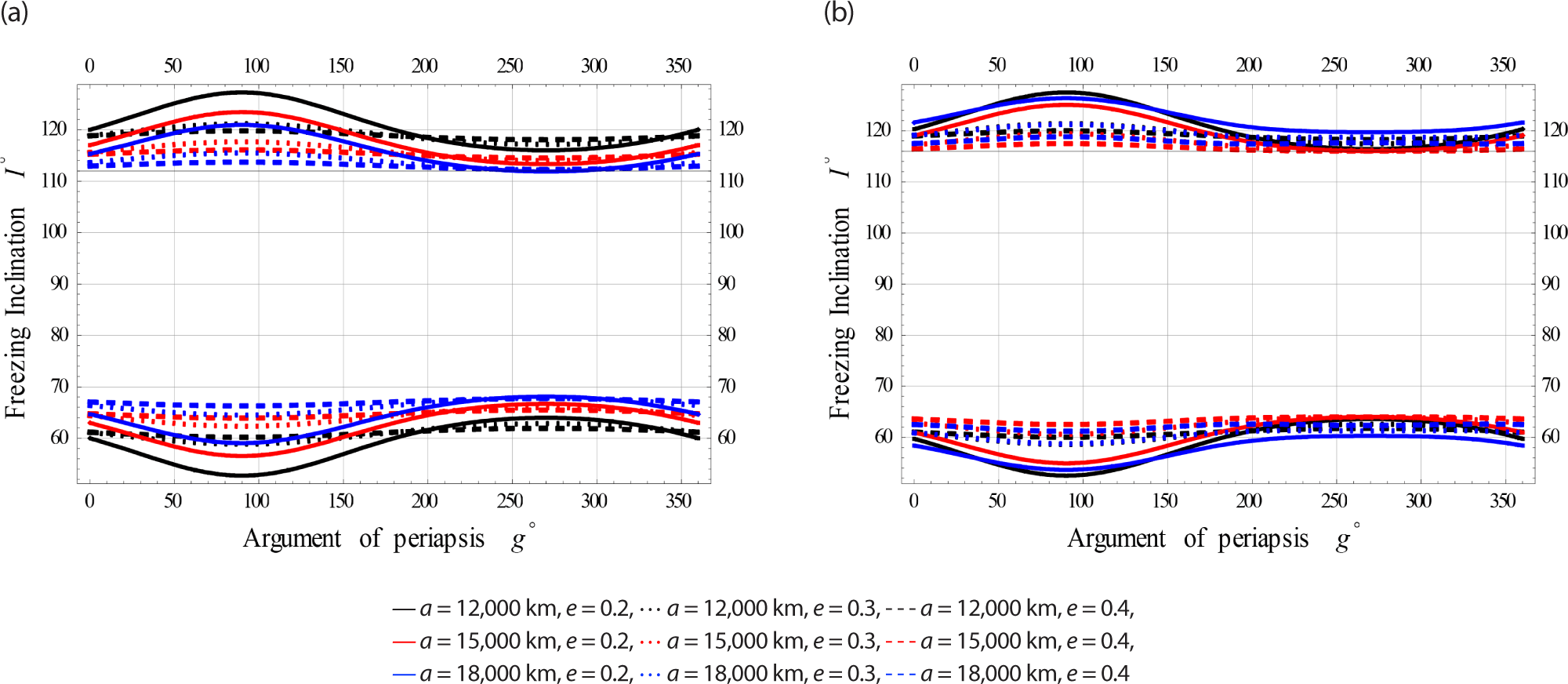
Fig. 4 simulate for Low Earth Orbits (in brief LEcO).
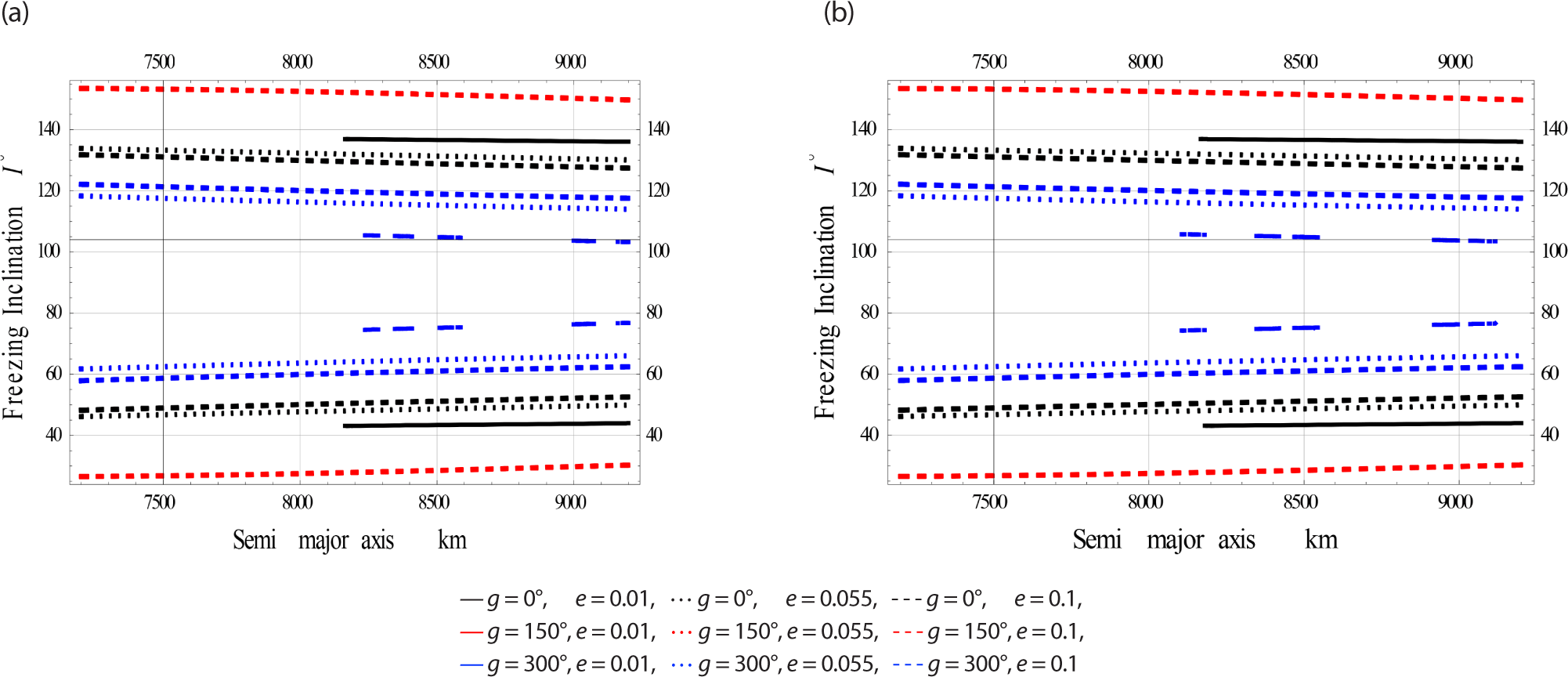
Fig. 5 simulate for Medium Earth Orbits (in brief MEcO).
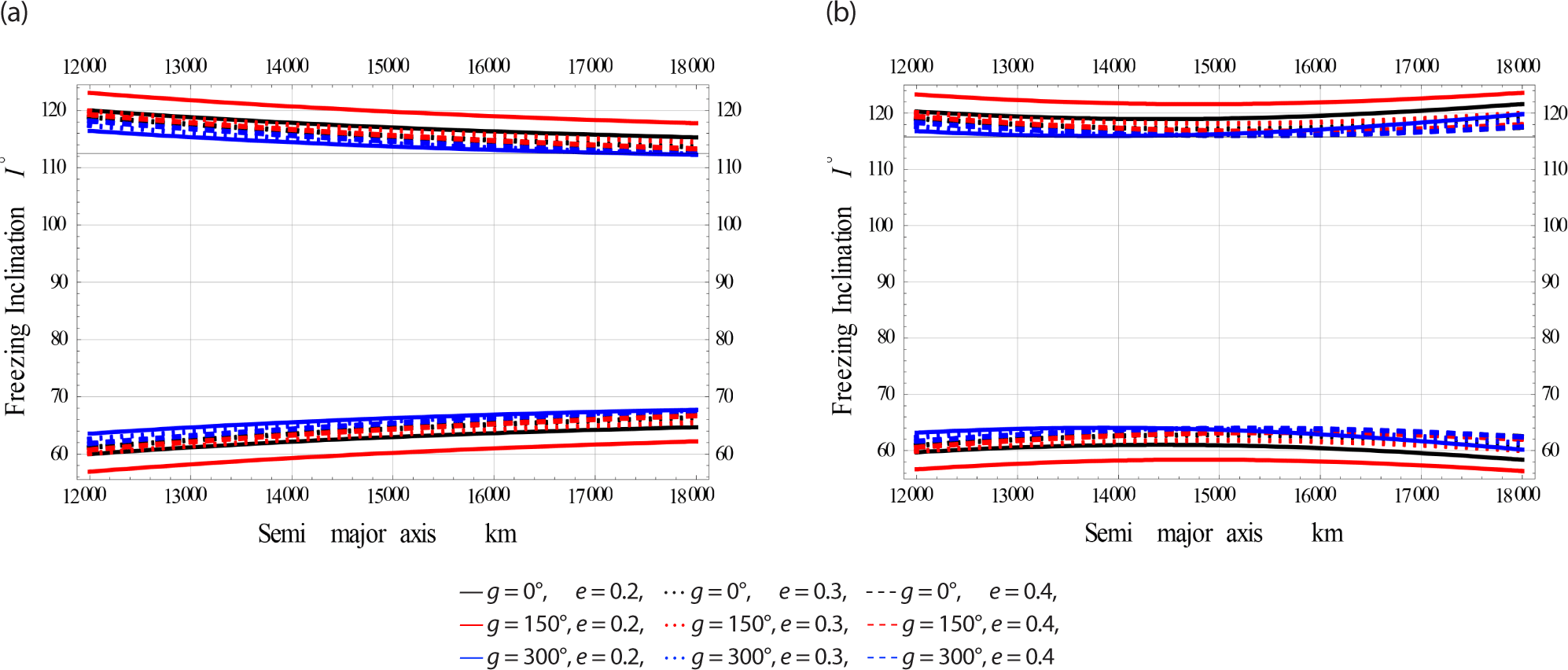
Fig. 6 simulate for High Earth Orbits (in brief HEcO).
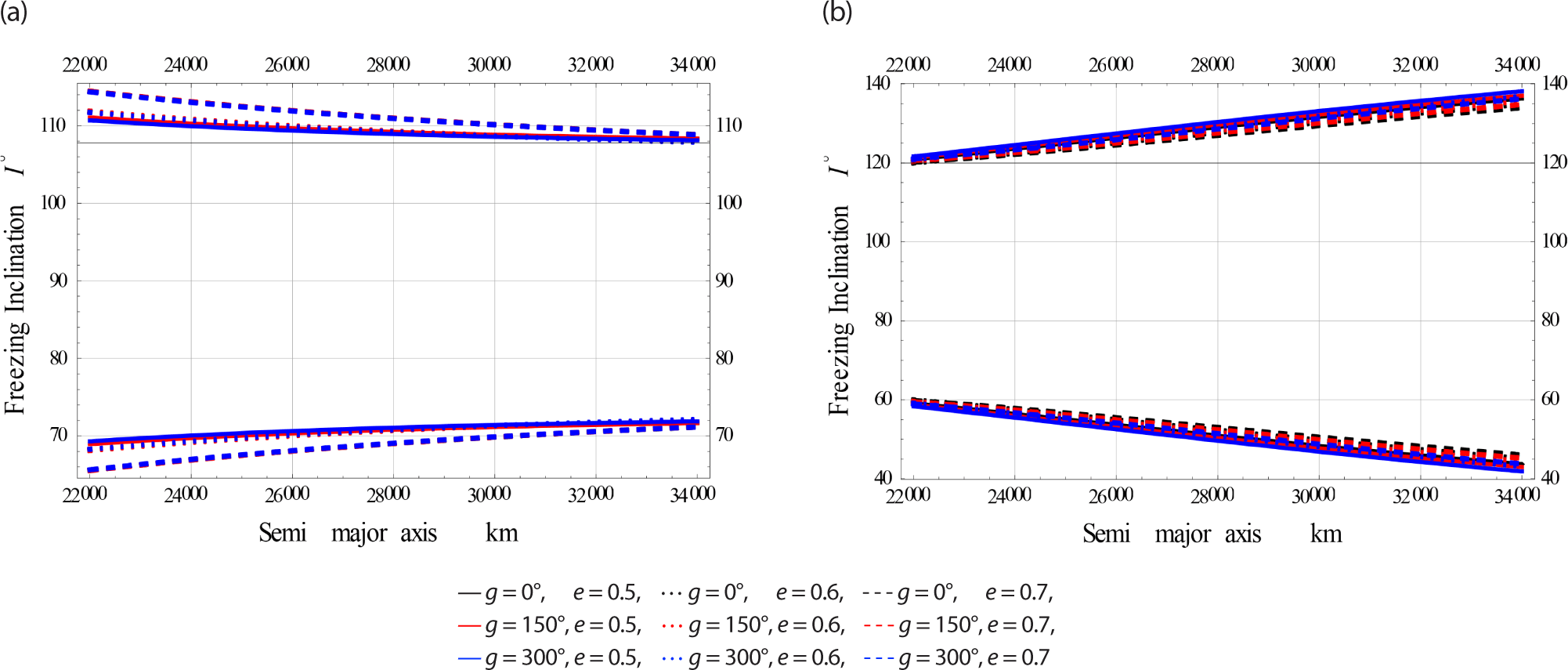
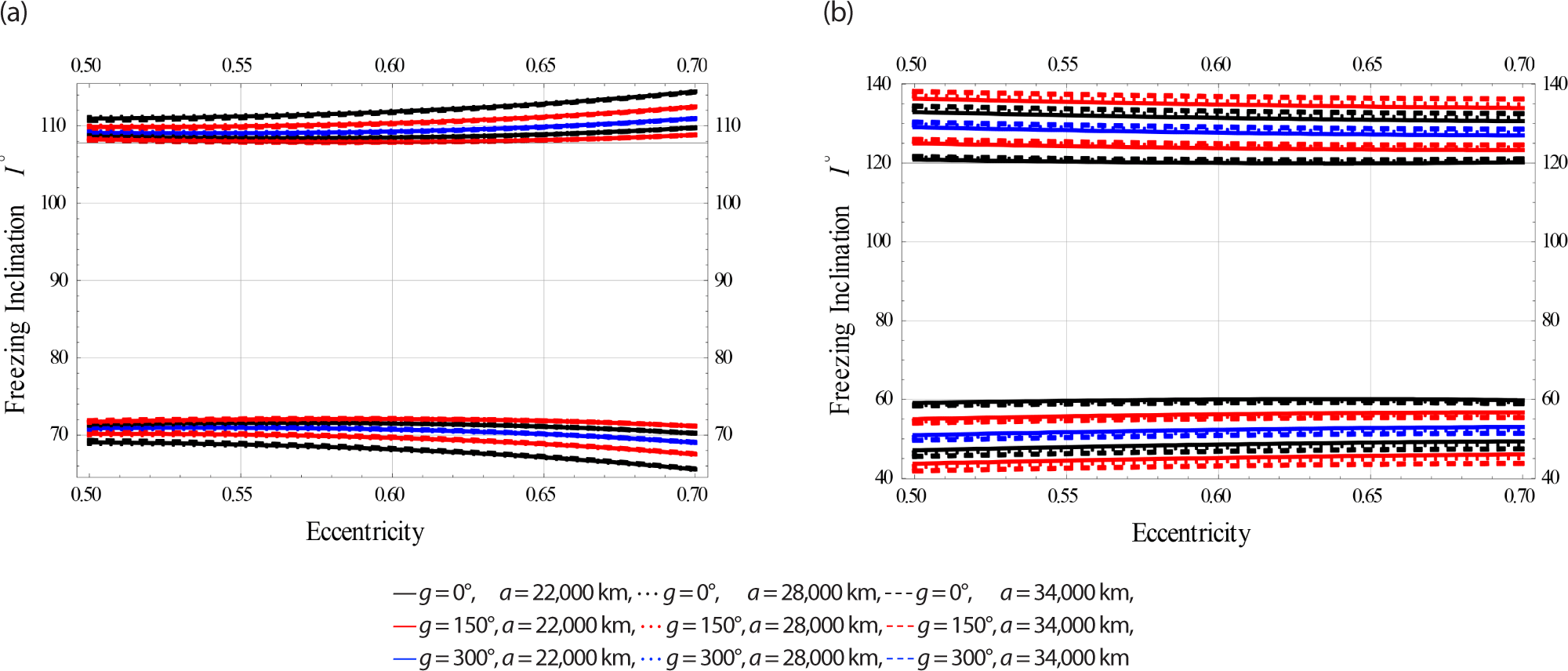
In the last case, we plotted the freezing inclination in degrees versus the third independent parameter, namely the eccentricity for three subcases; namely Low, Medium, and High Earth Orbits considering (GE) influence alone and combined with EM effects, respectively.
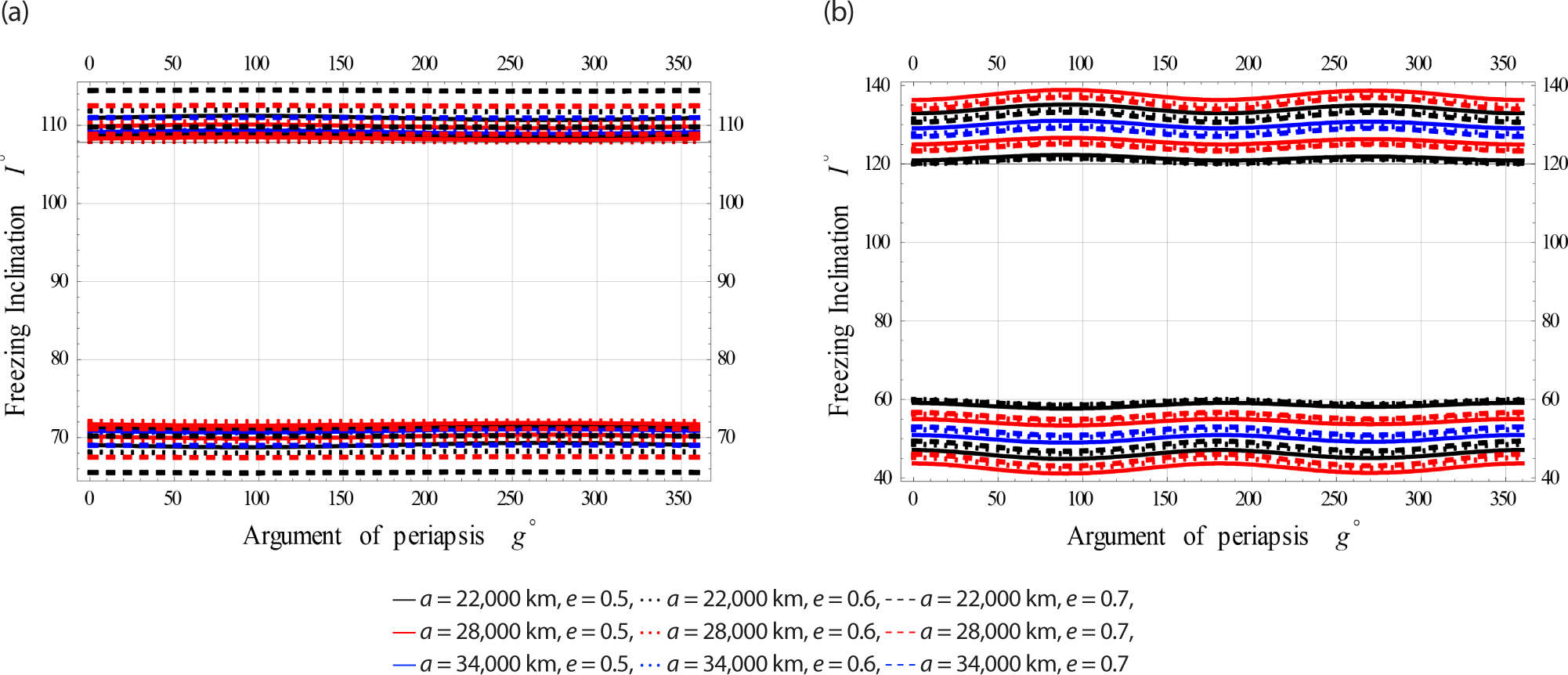
Fig. 7 are designed for Low Earth orbits.
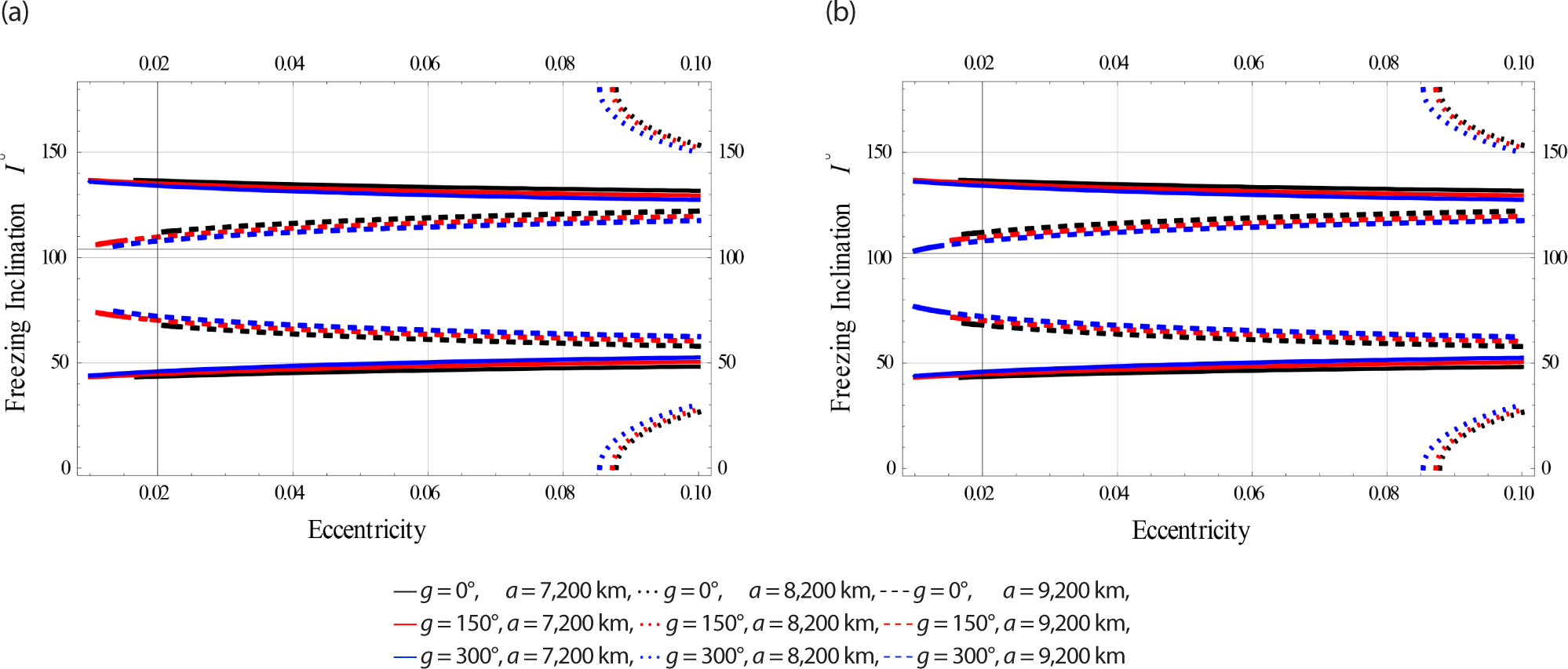
Fig. 8 have been done for Meduim Earth orbits.
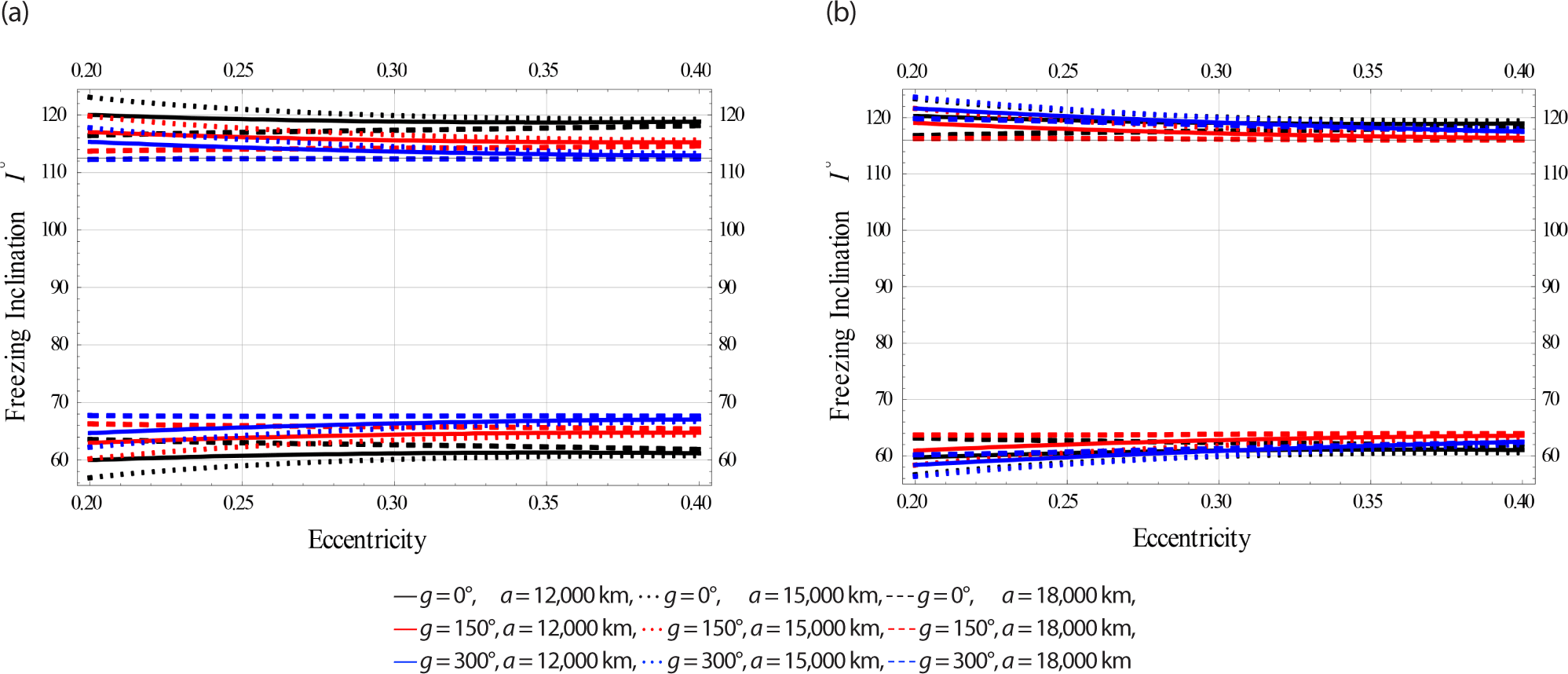
Fig. 9 have been done for High Earth orbits.
5. SOLUTION FOR THE ARGUMENT OF THE PERICENTRE
Eq. (4) is solved for the periapsis argument in this section. After a significant algebraic contribution, Eq. (4) may be rewritten as
with
6. DIFFERENT INVESTIGATED ORBITS OF EQ. (7)
In the following subsections, we will investigate three case studies, each of which contains three subcases. The first case studies the freezing ω versus I for three subcases; namely Low, Medium, and High Earth Orbits. The second case investigates the freezing ω versus the a for three subcases; namely Low, Medium, and High eccentricity Orbits. The third case studies the freezing ω versus e for three subcases; namely Low, Medium, and High Earth Orbits.
This section shows the the freezing ω (in degrees) concerning the orbital inclination.
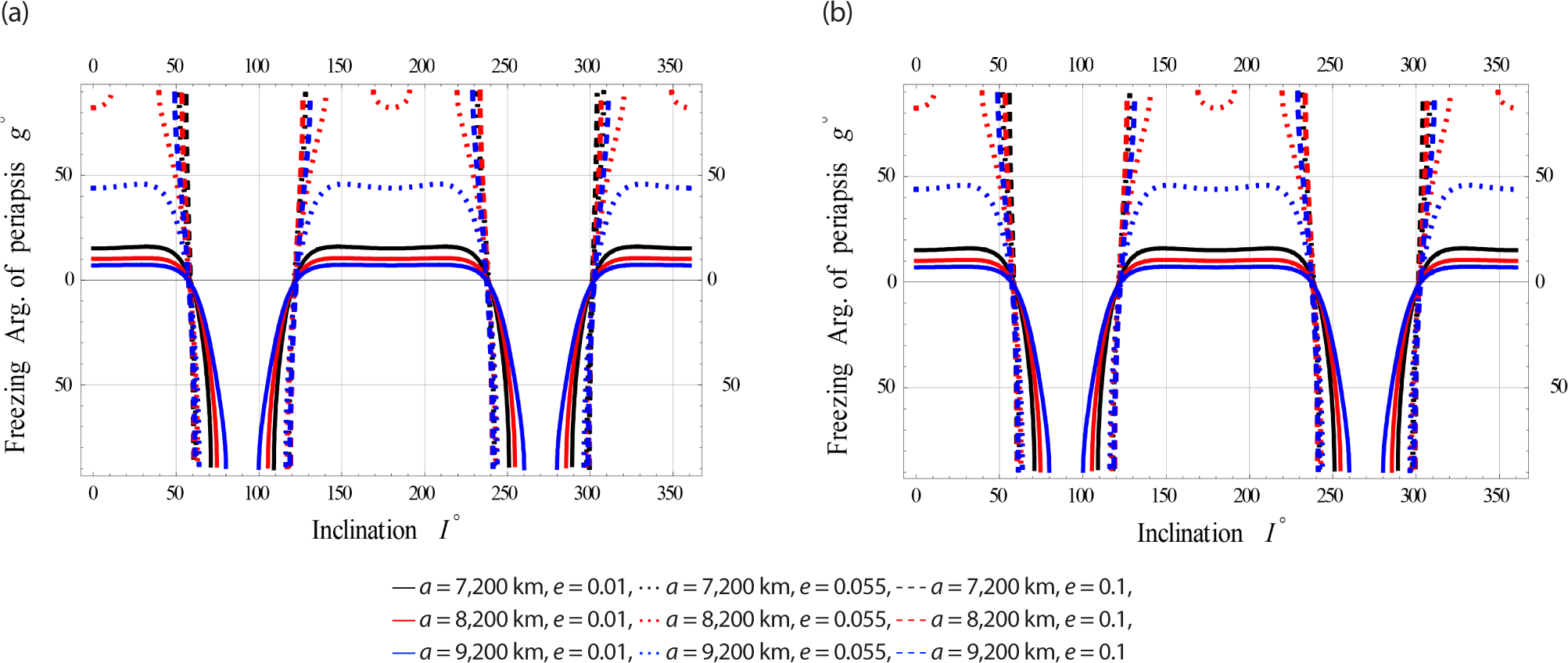
On Fig. 10, we plotted the freezing ω versus I for satellites at Low.
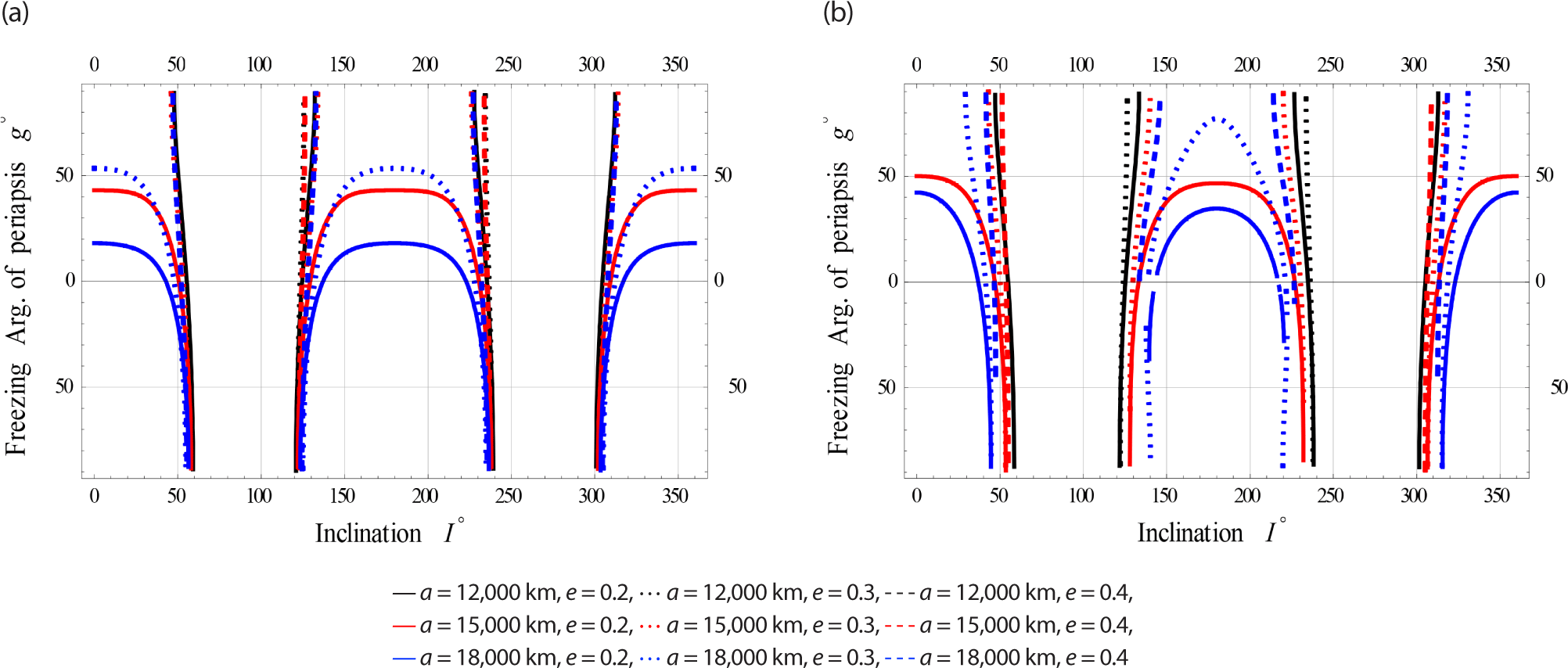
On Fig. 11, we plotted the freezing ω versus I for satellites at Meduim Earth Orbits respectively.
On Fig. 12, we plotted the freezing ω versus I for satellites at High Earth Orbits respectively.
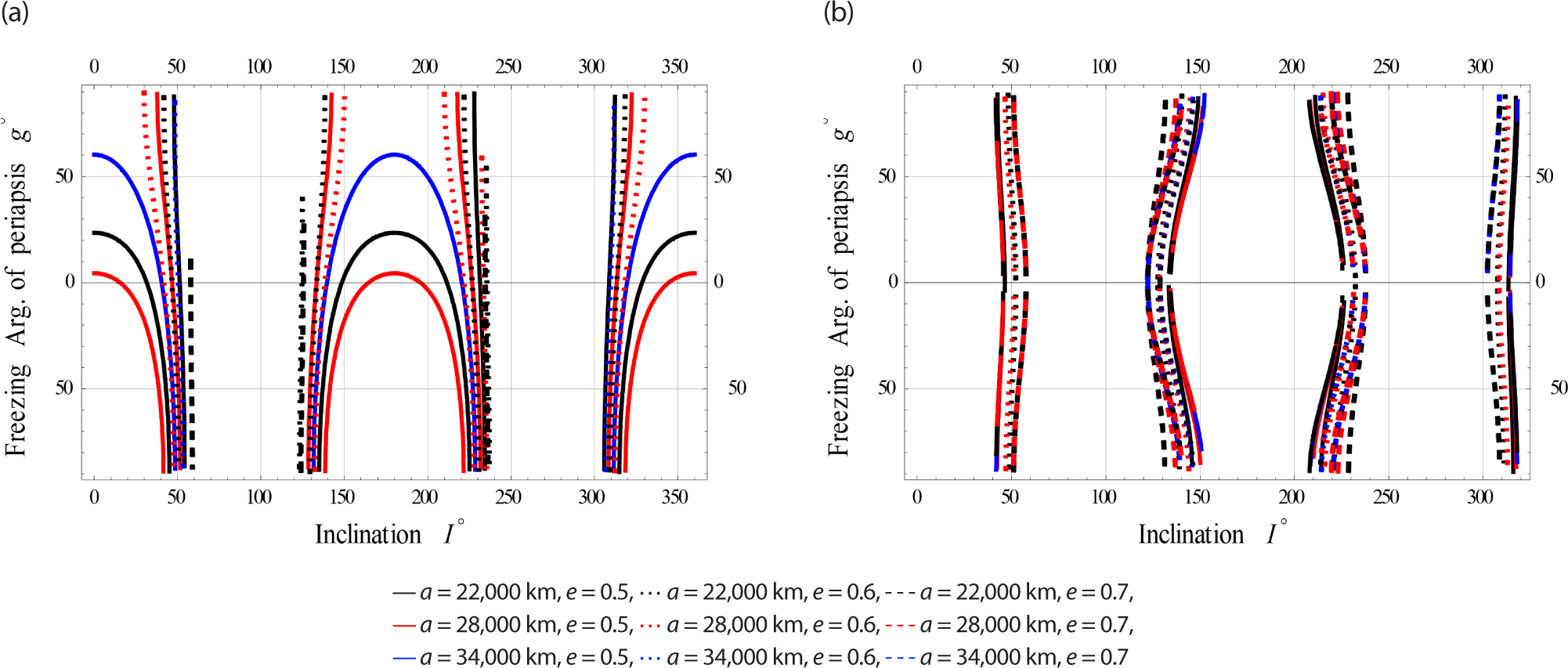
The (EM) perturbations on the dynamics of frozen orbits becomes worth, particularly in Medium and High Earth Orbits.
In this section we plotted the freezing ω versus some another independant parameter, namely the semi-major axis.
In Fig. 13, we plotted the freezing ω versus a for satellites at Low eccentricity Orbits. In this case the EM perturbation is very little, the dynamics shown in the Fig. 13(a) and (b) are nearly the same.
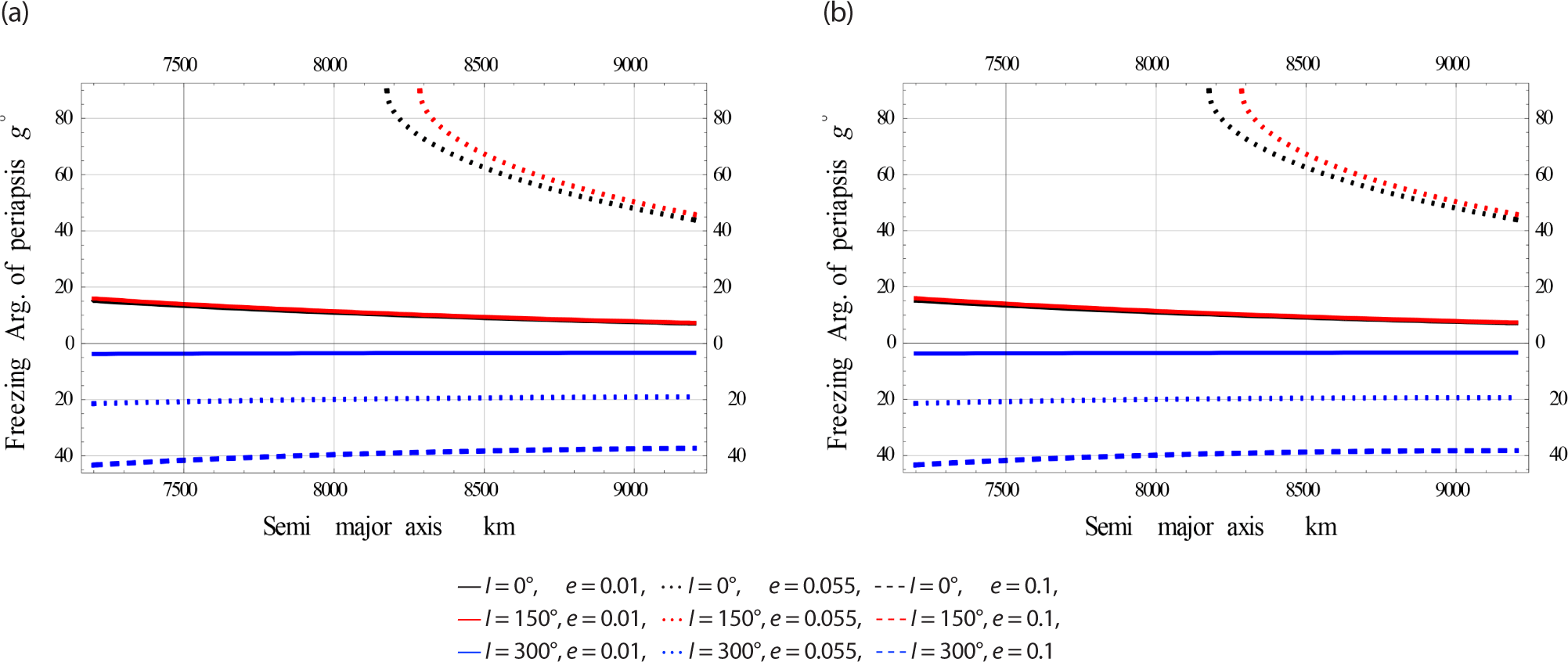
In Fig. 14, we plotted the freezing ω versus a for satellites at Meduim eccentricity Orbits.
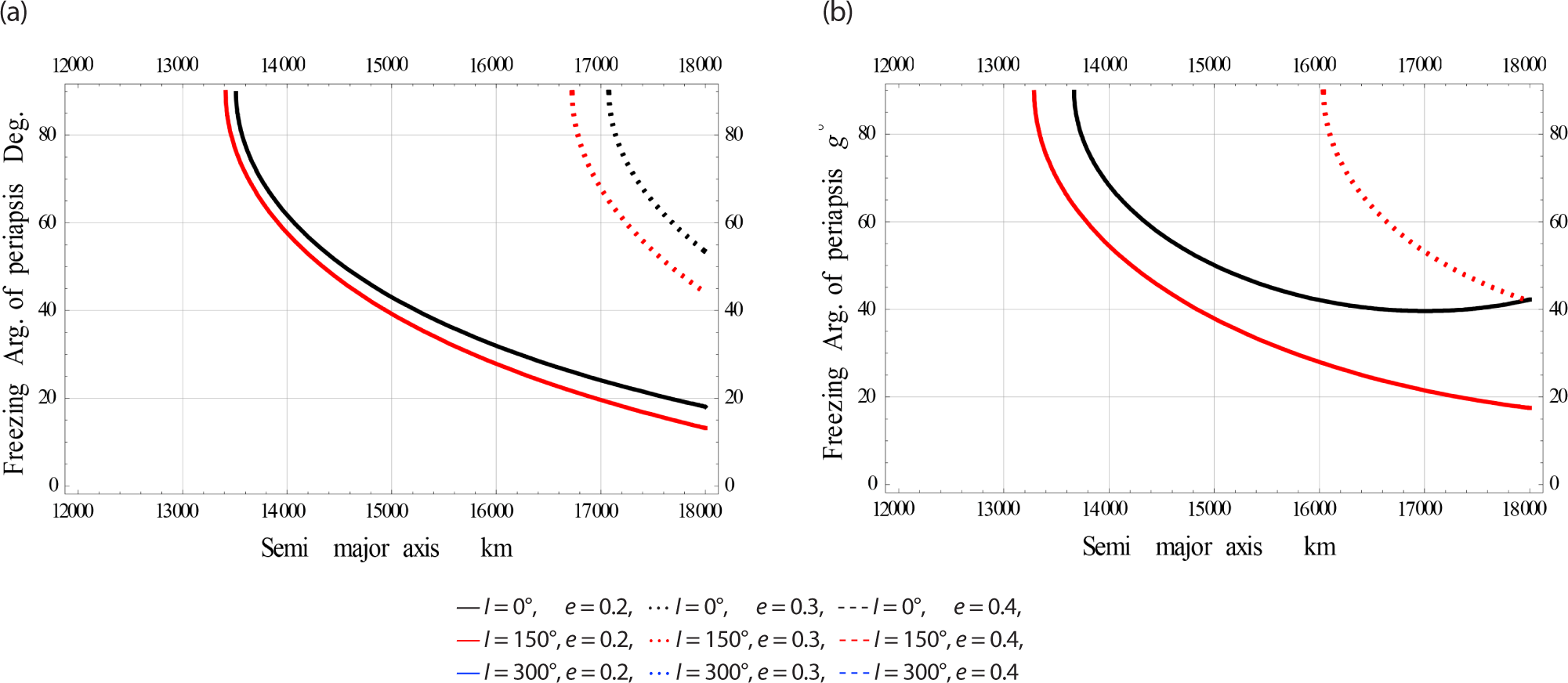
In Fig. 15, we plotted the freezing ω versus a for satellites at High eccentricity Orbits.
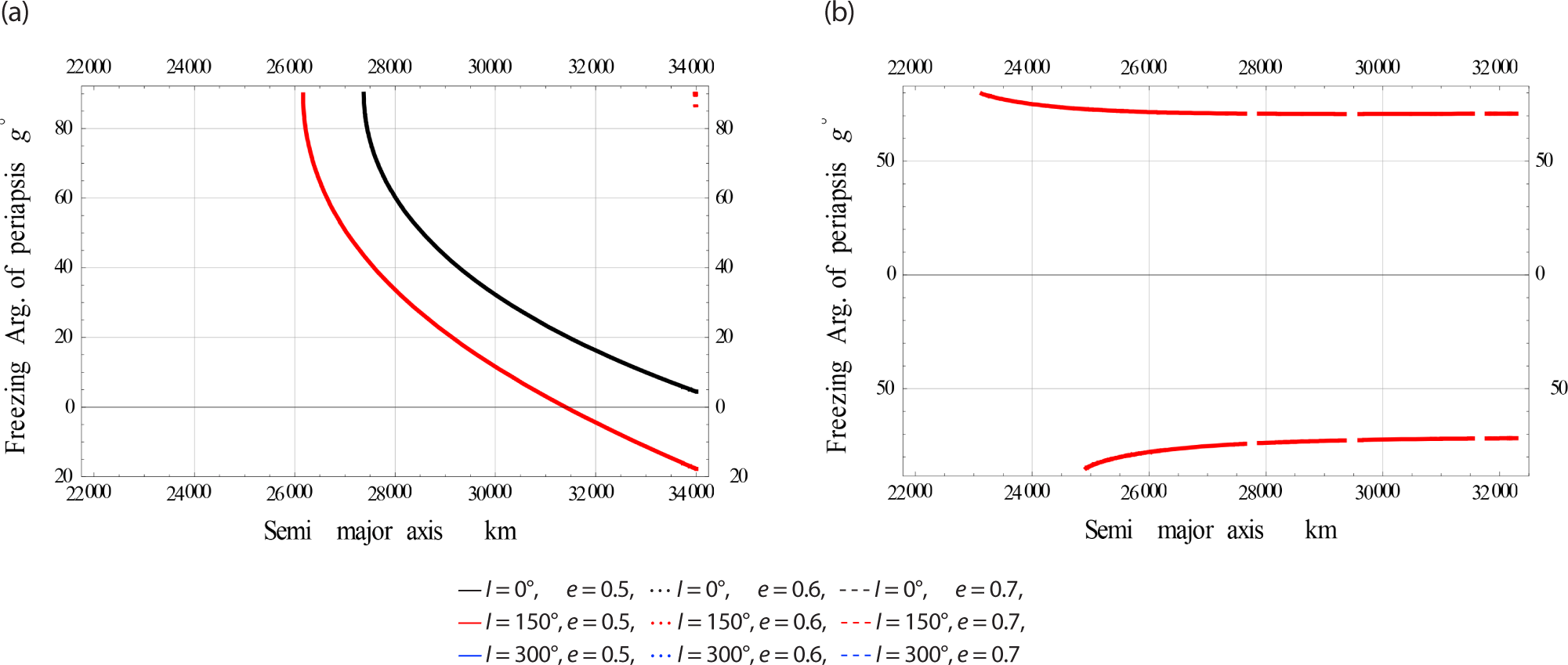
The effects on the frozen orbit dynamics when including the EM perturbations is clearly visible for MEcO and HEcO.
This section shows the the freezing ω (in degrees) concerning the orbital eccentricity.
In Fig. 16, we plotted the freezing ω versus for satellites at Low Earth Orbits.
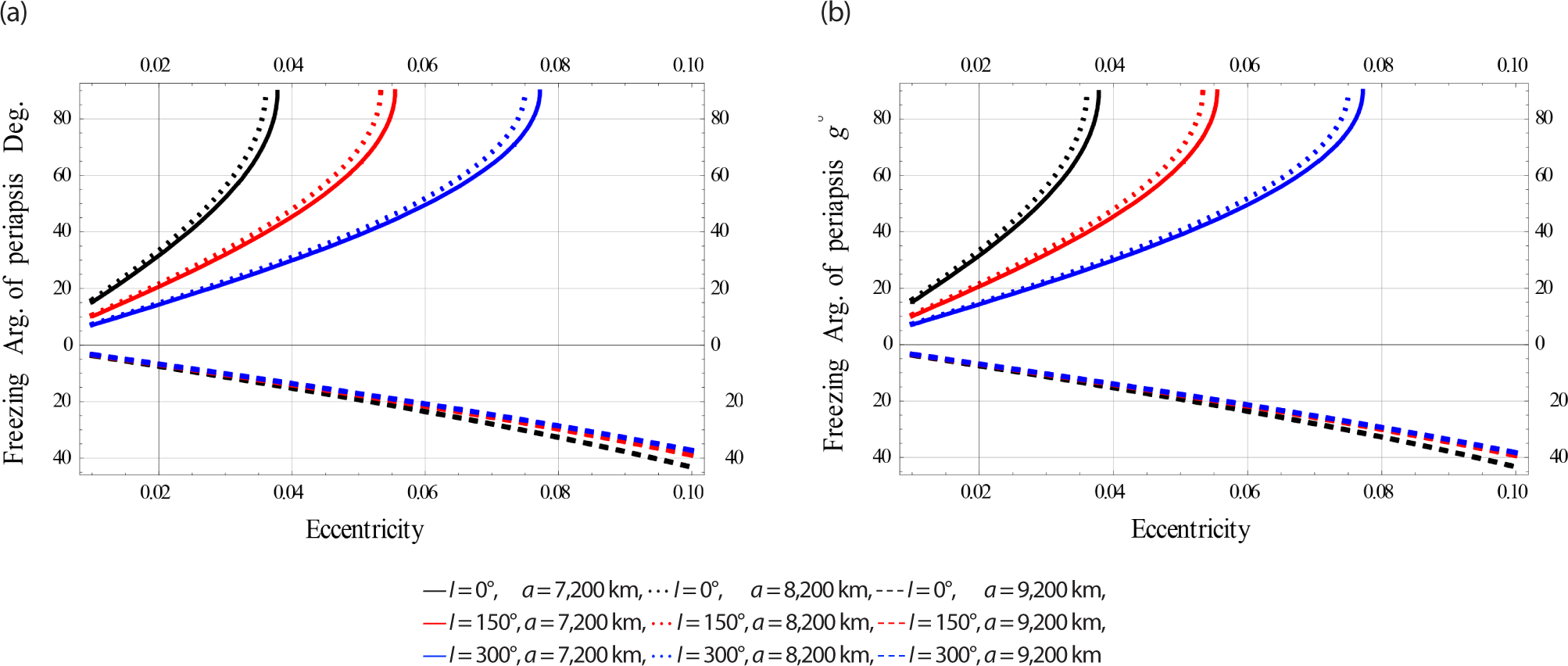
In Fig. 17, we plotted the freezing ω versus e for satellites at Meduim Earth Orbits.
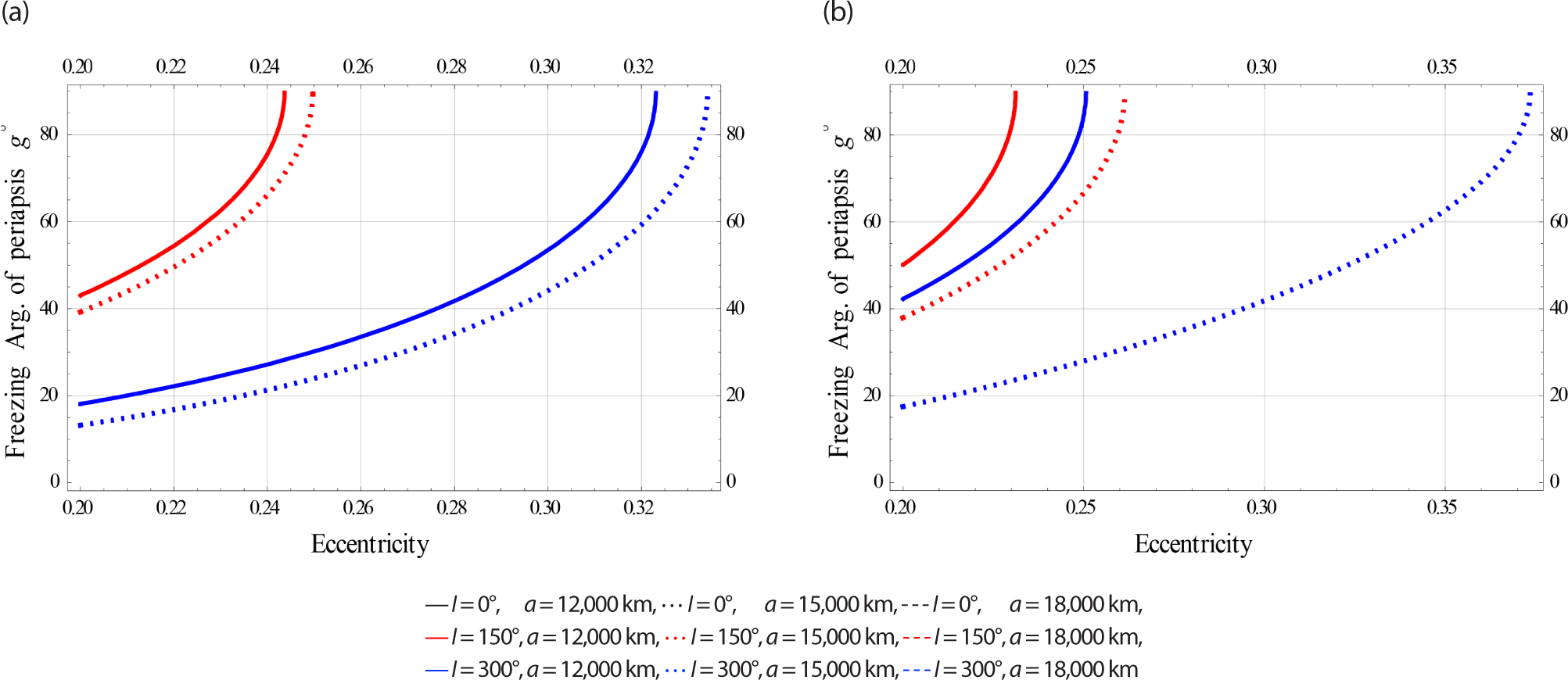
In Fig. 18, we plotted the freezing ω versus e for satellites at High Earth Orbits.
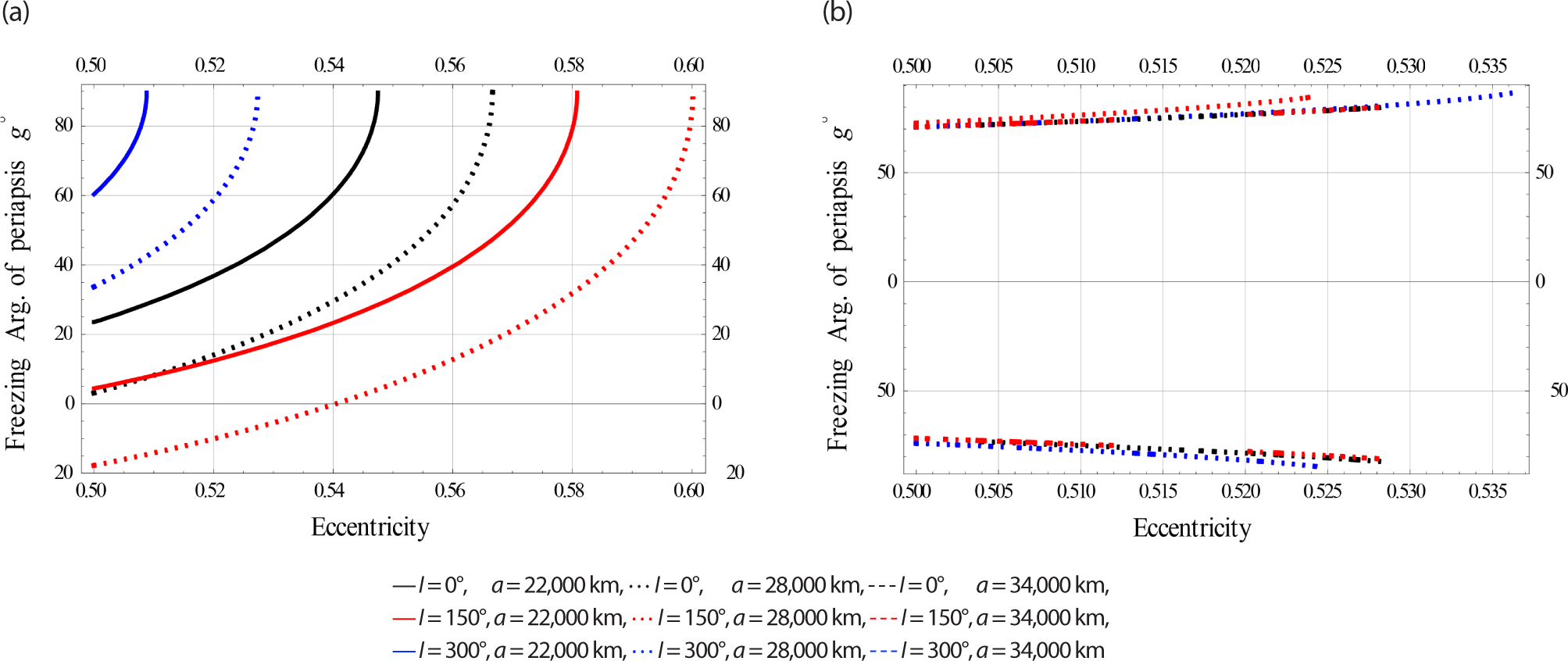
The effects of electromagnetic (EM) disturbances on frozen orbit dynamics become significant, especially in the medium and high earth orbits.
7. THE FROZEN ECCENTRICITY
In this part, we will get a family of eccentricity frozen orbits around the Earth by using transformed Hamilton (1).
Employ the Hamiltonian canonical equation of motion, where
Using the Delaunay variable and Eq. (10), we obtain
impose the eccentricity to be equal zero to capture the frozen eccentricity and rearrange the equation, thus
where
Using Eq. (12), to get, ė = 0 as
8. SOLUTION FOR INCLINATION
This section extends the concept of frozen eccentricity by manipulating the Hamiltonian equations in section 7 by considering the inclination parameter, demonstrating how freezing eccentricity can be achieved by using inclination as a parameter in the solution.
According to the powers of C, rewrite Eq. (11) as
where
In order to examine Eq. (15) in further detail, we will visualize it in the next section.
In order to visualize Eq. (15), we have found using MATHEMATICA software only two real roots of the algebraic Eq. (15). To freez the eccentricity we use the inclination as a freezing parameter. Three-dimensional graphs of the freezing inclination against two parameters (the semi-major axis and the eccentricity) are presented in Figs. 19(a) and (b), using three different values for the argument of periapsis. Also, other graphs are introduced against two parameters (the semi-major axis and the the argument of periapsis) in Figs. 19(c) and (d), using three values of eccentricities.
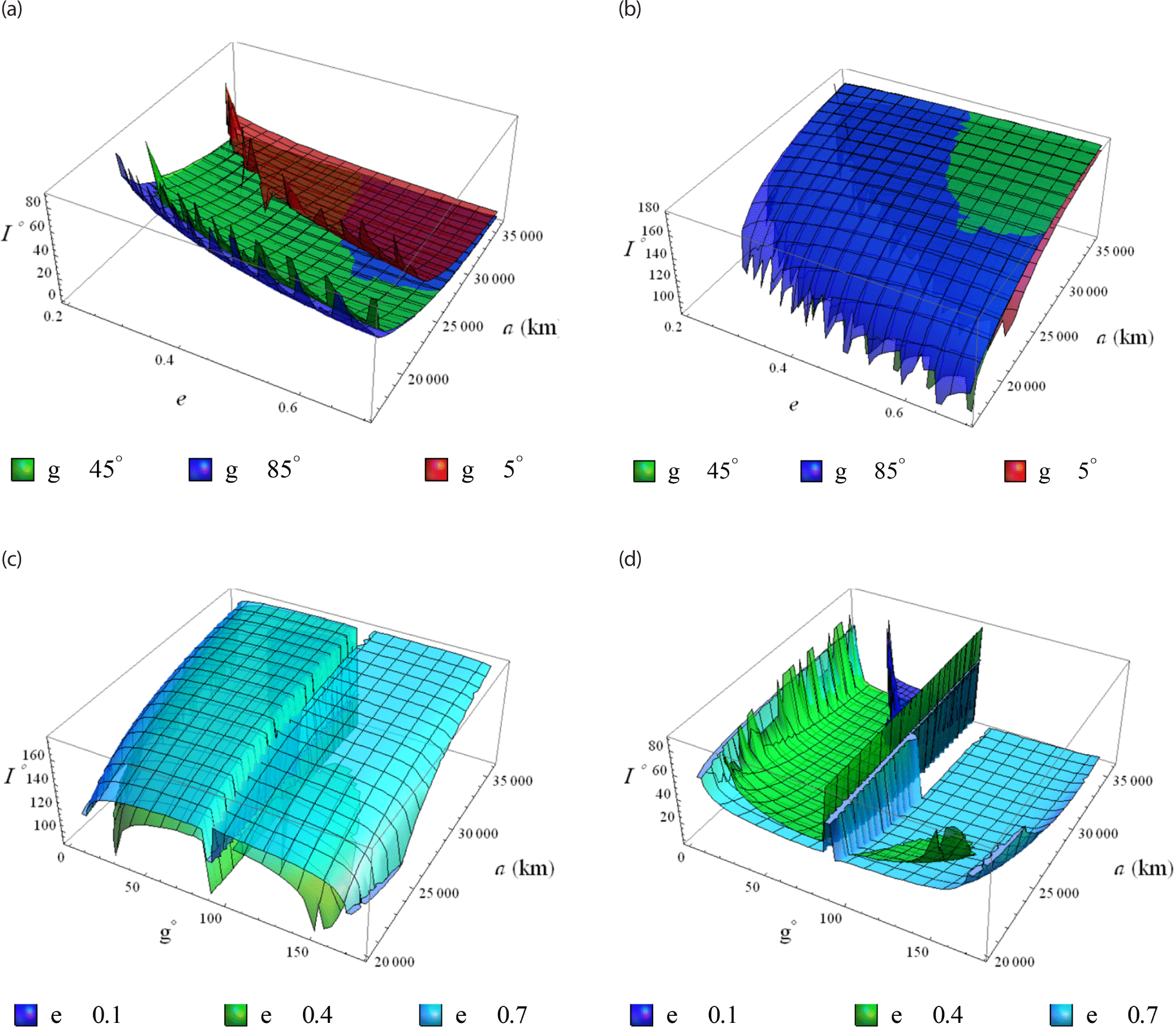
Remark. Each two real roots of Eq. (15) will not close up the whole domain of the inclination or the argument of periapsis smoothly, it is very clear from the wavy edges of each root. This is due to the fact that the the frozen orbits are equilibruim solutions at some critical values of the orbital elements; e.g. critical inclination. This ensures that there exist a bifurcation structure near to these critical values.
Use the non-singular variables to define the eccentricity vector’s polar coordinate as:
where ė, ġ are given by
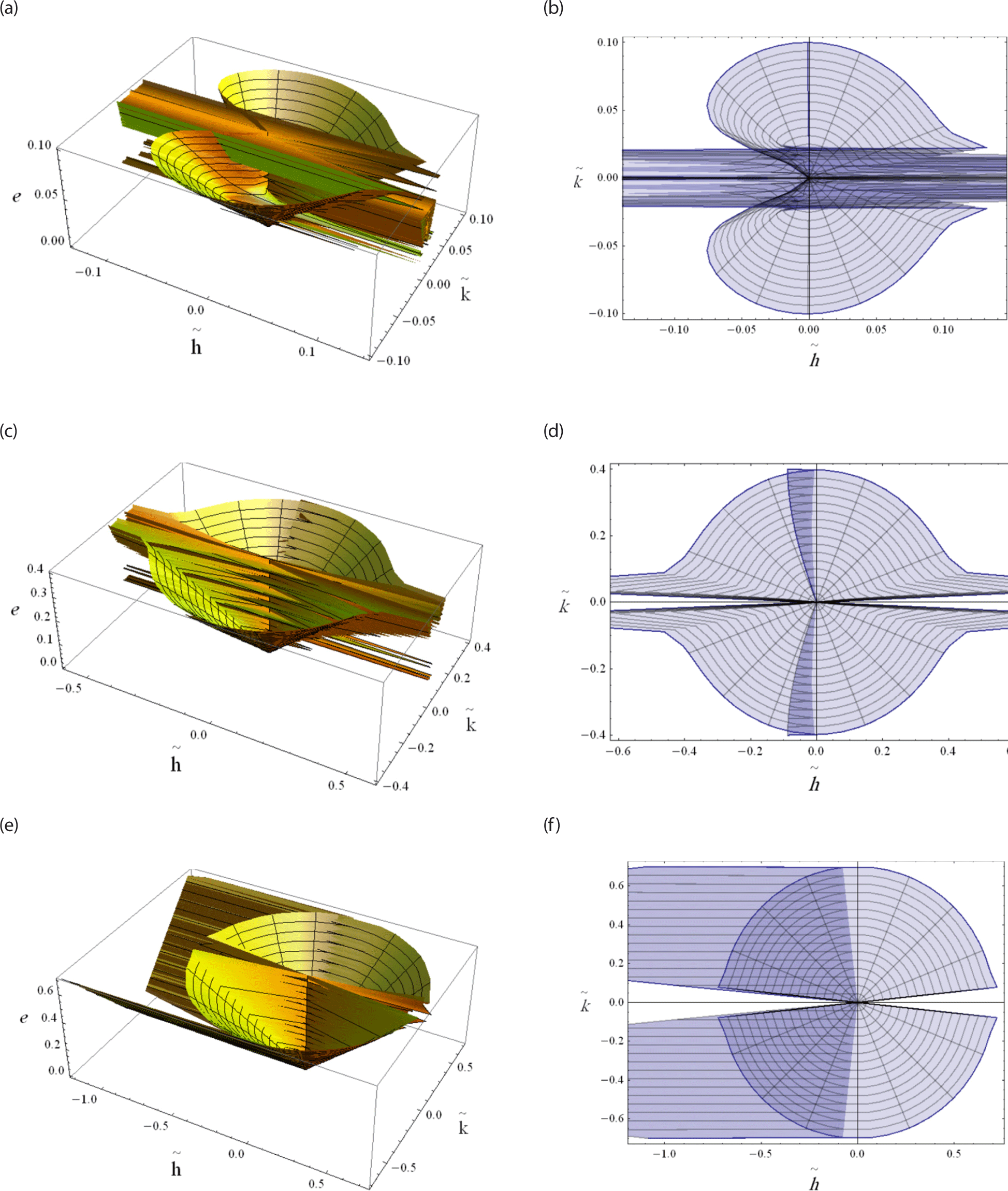
Interpreting the phase space of the eccentricity vector provides a comprehensive understanding of the orbital dynamics. It allows for predictions about the long-term evolution of orbits, helping to assess the stability and sustainability of orbits over extended periods. Also, t can reveal invariant manifolds that remain unchanged despite gravitational perturbations which associated with stable or unstable orbits.
The eccentricity vector locus using the nonsingular variables () is represented either as a 3D and 2D projection onto () plane. In Fig. 20(a) the behaviour of the eccentricity vector is visualized for low earth orbits a = 7,200 km as well as for a very narrow range of eccentricity e ∈ [10–20, 0.1]. Its corresponding projection onto 2D is shown in Fig. 20(b). In Fig. 20(c), similar illustrations are obtained for the meduim a = 15,000 km Earth orbits, but with a relatively wide range of eccentricity e ∈ [10–20, 0.4]. The corresponding projection onto 2D is dipicted in Fig. 20(d). Finally in Fig. 20(e) similar illustrations are obtained for the high a = 36,000 km Earth orbits, but with a wide range of eccentricity e ∈ [10–20, 0.7]. The corresponding projection onto 2D is dipicted in Fig. 20(f).
9. CONCLUDING REMARKS AND FUTURE WORKS
Section 1 of this book provides a brief introduction that focuses on earlier research in the topic of study. The focus is on the key components of the current work. Section 2 provides the initial normalized Hamiltonian, which is then used in the following sections to compute several families of the long-term frozen orbits of a charged satellite in the relevant model in the subsequent sections 4, 5, 6, 7, 8, 9 and 10. To study these obtained frozen orbits MATHEMATICA CODE is constructed. Using the inclination as a freezing parameter, some kinds of orbits ranges from a very low Earth orbits to a very high Earth orbits and enjoy a very low eccentricity to very high eccentricity are invistigated see Figs. 1–9. The same is done for considering the argument of periapsis as a freezing parameter, see Figs. 10–18 and their analysis. The ranges that guarantee the frozen orbits are deduced from the figures.
See Fig. 19 for three-dimensional representations of the freezing inclination versus the semi-major axis and the eccentricity (as shown in Figs. 19(a) and (b)) and versus the semi-major axis and the argument of periapsis (as shown in Figs. 19(c) and (d)). Using the non-singular variables (), the eccentricity vector’s phase space is represented. Three dimentional plots and its projection onto () plane are analyzed, see Fig. 20. In all the investigated cases, the effect of EM field on the freezing inclination of a charged satellite is clearly visible.
In the future, we aim to employ our model in actual space missions conducted within its orbital framework to refine the model based on observational data gathered from these missions. Additionally, our objectives include enhancing the realism of the model through the following measures:
-
Incorporating the Poynting–Robertson drag force to account for the influence of charged particles.
-
Investigating the impacts of EM field communication satellites when they are charged and operational within the ionosphere.
-
Examining bifurcation surfaces within a comprehensive parameter space, alongside exploring the evolution of families in relation to physical parameters, inclination, and eccentricity.
-
Applying the study to motion around prolate bodies, particularly in light of recent missions to variously shaped objects within the solar system.
