Fundamentals of Numerical Modeling of the Mid-latitude Ionosphere

1. INTRODUCTION

The ionized part of the upper atmosphere, the ionosphere, is one of the key components of the space weather. The upper atmosphere including the mesosphere, the thermosphere and the ionosphere is the closest part of the space environment to the Earth and most directly affects human activity not only in space but also on the ground. The altitude of the ionosphere ranges from about 60 km to about 1,000 km, which coexists with the neutral atmospheric regions of the mesosphere, the thermosphere, and the exosphere. The ionospheric plasma is affected by various physical processes such as chemical reactions, diffusion, wave disturbances, plasma instabilities, and transports associated with neutral wind and electric and magnetic fields. These processes are strongly coupled to other regions of the Earth’s atmosphere such as the lower atmosphere, the thermosphere, the plasmasphere, and the magnetosphere.

The existence of the ionosphere is also of great importance in the Earth’s atmosphere. Although the plasma density (i.e., electron density) of the ionosphere is only about 0.1% of the neutral density at the altitude of ionospheric peak density, the existence of the ionospheric plasma greatly influences the thermal and dynamical characteristics of the upper atmosphere in association with the Earth’s magnetic field. Since the charged particles tend to move only along the magnetic field lines, the ionospheric plasma acts as a resistance to the motion of the neutral particles in the direction perpendicular to the magnetic field lines: for instance, the zonal component of the thermospheric wind in the low and mid-latitude regions feels significant amount of drag force due to the ionospheric plasma (e.g., Martinis et al. 2001). In the mid-latitude region, the ionosphere is closely coupled to the plasmasphere to refill the plasmaspheric flux tubes after storm-time erosion of plasmaspheric plasma and for the nighttime ionosphere to be maintained by downward flux from the plasmasphere (e.g., Jee et al. 2005; Lee et al. 2013).

The role of the ionosphere becomes even more important in the polar region by absorbing various forms of the solar wind energy stored in the magnetosphere and then by transporting them to the global neutral atmosphere. The polar ionosphere is electromagnetically connected to the magnetosphere via geomagnetic field lines and absorbs not only the electrical energy generated in the solar wind-magnetosphere interactions but also energetic particles existing within the magnetosphere or entering directly from the solar wind. These forms of energy greatly affect the ionosphere-thermosphere system in the polar region and can propagate into the lower latitude region (e.g., Heelis 1982; Fontaine 2002; Kim et al. 2020). On the other hand, the ionosphere can have substantial impacts on the magnetosphere by providing an important source of the magnetospheric plasma (e.g., Welling et al. 2016) and by controlling the electric current system within the magnetosphere (e.g., Ridley et al. 2004; Bhattacharya et al. 2022). Therefore, the ionosphere needs to be routinely monitored from both the ground and space and also needs to be modeled by solving physical equations governing the ionosphere in order to understand the observed variabilities in association with relevant external forcings (e.g., Prölss 2004; Jee et al. 2005; Schunk & Nagy 2009).

In this review, typical approaches of modeling the ionosphere will be introduced (Section 2) with fundamentals of the numerical modeling of the ionosphere using simplified equations governing the ionosphere (Section 3). Then specific partial differential equation will be derived from the governing equations for the mid-latitude ionosphere with required boundary conditions (Section 4). Finally, a numerical solution for the differential equation will be provided in Section 5.

2. IONOSPHERIC MODELS

Modeling of the ionosphere is critical not only for the specification and forecast of ionospheric weather, but also for the understanding of various physical processes occurring within the ionosphere (e.g., Schunk & Sojka 1996; Schunk et al. 2003). There are several approaches for the ionospheric modeling but they can be largely categorized into three types: empirical, theoretical, and data assimilation models. Empirical models represent the climatological behavior of the ionosphere by incorporating various ionospheric data. Since they rely on observations, however, the capability of empirical models is limited to certain geophysical conditions at which the observations are available for the model. Currently, the most comprehensive and widely available empirical model for the ionosphere is the International Reference Ionosphere (IRI). The IRI was initiated in 1968 as an international project sponsored by the Committee on Space Research (COSPAR) and the International Union of Radio Science (URSI). Since then, the IRI model has been continuously improved and updated. The most recent version (IRI-2020) is able to produce various ionospheric parameters, such as electron density, ion densities (O⁺, H⁺, He⁺, NO⁺, O₂⁺), electron and ion temperatures, equatorial vertical ion drift, and total electron content (TEC) (Bilitza 2005; Bilitza et al. 2022 and references therein).

Physics-based models calculate ionospheric parameters by numerically solving the governing equations such as continuity, momentum, and energy equations for the ionospheric electron and ions. To solve these equations, it requires several input parameters which are mostly related to other regions of the upper atmosphere, including the neutral atmosphere, the plasmasphere and the magnetosphere, and the electrodynamics at low and high latitudes. The typical input parameters include neutral parameters such as density, temperature, and winds; high-latitude convection electric fields and particle precipitation; low-latitude electric fields; and lower atmospheric waves such as gravity wave, planetary wave, and tidal wave. These model inputs are typically provided by adopting empirical models. This type of model includes the ionosphere forecast model (IFM) developed at Utah State University (Schunk et al. 1997) and Sami2 is Another Model of the Ionosphere (SAMI2/SAMI3) (Huba et al. 2000; Huba & Krall 2013; Huba et al. 2017). An alternative approach to obtain the input parameters is to couple the ionospheric model to physics-based models for the neutral atmosphere and the electrodynamics at low and high latitudes. Since they are closely coupled with the ionosphere, this approach can calculate the ionospheric parameters in a more physically self-consistent way and therefore provide a useful tool of analyzing the model results in connection with the coupling processes among these regions. In addition to its complexity and high computational cost, however, the coupling approach can produce significant uncertainties in the model results because errors can propagate from one model to the other and enhance their effects throughout the model calculation. Nonetheless, the coupled models are essential to correctly specify the ionosphere-thermosphere system as our understanding of the system deepens with enhanced availability of the observations so that it will be coupled to the models for the other parts of the space environment and used eventually for the development of the space weather forecast model (e.g., Shim et al. 2018; Scherliess et al. 2019). Models adopting this coupling approach include the National Center for Atmospheric Research (NCAR) Thermosphere-Ionosphere-Mesosphere-Electrodynamics General Circulation Model (TIME-GCM) (Roble 1996), Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics Model (CTIPe) (Codrescu et al. 2012), Global Ionosphere-Thermosphere Model (GITM) (Ridley et al. 2006) etc. Recently, the coupling is expanding further to the lower atmosphere as well as the magnetosphere. For example, the NCAR Whole Atmosphere Community Climate Model with thermosphere and ionosphere extension (WACCM-X) is the extended version of the WACCM for the lower atmosphere by extending to the upper atmosphere of the ionosphere and the thermosphere (Liu et al. 2018). Most recently, the global magnetohydrodynamic (MHD) model of the magnetosphere, which is the Grid Agnostic MHD with Extended Research Applications, is coupled to the Rice Convection Model (RCM) of the ring current and Thermosphere-Ionosphere Electrodynamics General Circulation Model (TIEGCM) of the upper atmosphere to construct a coupled geospace model for simulating critical mesoscale structures in the geospace system during storms (Lin et al. 2021). These types of the coupled models for various parts of the space environment should be of fundamental importance to eventually develop the space weather forecast model as well as for more complete understanding of the regions, in association with data assimilation techniques as can be described below.

Although empirical and theoretical models have been extensively utilized for both practical and research purposes, their capabilities of ionospheric specification and forecast are still fairly limited largely due to the uncertainties in the external forcing parameters, in addition to the lack of observed data. The external forcing parameters, including the neutral composition, winds and temperatures, the low-latitude electric fields, the convection electric fields and particle precipitation at high latitudes, and lower atmospheric waves, are not well specified, especially for geomagnetically disturbed conditions. With respect to the observations of the ionosphere, most of the ground-based observations are concentrated in the northern hemisphere and the space-based observations are not yet sufficient to cover all geophysical conditions. To achieve the best model results out of the limited knowledge of the ionosphere from the theoretical and observational studies, the direction of the modeling is heading towards physics-based data assimilation models. By using physics-based models, available measurements, and sophisticated assimilation techniques to combine them, this approach is able to produce not only the specification of the ionosphere, but also ionospheric weather forecasts by adopting real-time measurements. The efforts to develop this type of model include the Global Assimilation of Ionospheric Measurements (GAIM) developed by Utah State University (Scherliess et al. 2004, 2006; Schunk et al. 2004, 2020) and a model using the WACCM-X and the Data Assimilation Research Testbed (DART) developed from the result of NCAR’s Data Assimilation Initiative (Pedatella et al. 2020).

In the following sections, we will briefly go through the fundamental equations describing the ionospheric density and partial differential equation for major ion (O⁺) in the ionosphere with boundary conditions required to numerically solve the equation.

3. MODEL EQUATIONS

In the region of the ionosphere where the diffusion approximation is valid (slowly varying, no wave phenomena considered, ∂u_j/∂t → 0; and subsonic flow, u_j·∇u_j → 0), the momentum and continuity equations for the plasma can be expressed as

where subscript n corresponds to neutrals and subscript j to either ions or electrons, p_j = n_jkT_j is the partial pressure, τ_j is the stress tensor, g is the gravitational acceleration, P_j is the ionization production rate, L^′_j is the ionization loss frequency, ν_jn is the momentum transfer collision frequency for neutrals and electrons or ions, and Coulomb collisions are neglected. Assuming only one ion species (O⁺), charge neutrality (n_e = n_i), and zero current (n_eu_e = n_iu_i), the ion momentum equation along the magnetic field line reduces to the ambipolar diffusion equation

where subscript i is for ions, T_p = (T_i + T_e)/2 is the plasma temperature, D_a = 2kT_p/m_iν_i is the ambipolar diffusion coefficient, and ν_i = ∑_k ν_ik is the momentum transfer collision frequency for ions and neutrals. In the derivation of the ambipolar diffusion Eq. (3), it is assumed that all the neutrals have a common drift velocity u_n in the ionosphere. In the vertical direction z, for example, the equation can be expressed in the form

Note that the ion-neutral collision frequency v_in is basically proportional to the neutral density, and thus the diffusion coefficient D_a is inversely proportional to the density. Therefore, D_a exponentially increases with altitude since the neutral density decreases exponentially with altitude. The last term in Eq. (4), as a consequence, becomes negligible with increasing altitude. If the stress term is neglected, the equation reduces to the classical diffusive equilibrium equation

where H_p = 2kT_p / m_ig is the plasma scale height. Under the isothermal ionosphere (i.e., constant T_p) in the diffusive equilibrium, the major ion (or electron) density decreases exponentially with altitude at a rate of the plasma scale height as can be expressed as

where the subscript 0 corresponds to a certain reference altitude.

4. PARTIAL DIFFERENTIAL EQUATION FOR THE MID-LATITUDE IONOSPHERE

The ambipolar diffusion Eq. (3) can be applied along the magnetic field lines for strongly magnetized ionosphere and also in the vertical direction for unmagnetized ionosphere. Considering the vertical components of induced plasma drifts due to an eastward electric field, an equatorward meridional neutral wind, and field-aligned plasma diffusion driven by vertical forces (e.g., gravity, temperature gradient, and density gradient), the vertical component of the ion diffusion equation becomes

where I is the inclination or dip angle of the geomagnetic field and the ∇ · τ_j term is neglected for simplicity. The parameter z is the vertical coordinate, which is positive in the upward direction. Fig. 1 shows the vertical components of the plasma drifts by an electric field, neutral wind, and vertical forces. In this expression for the vertical ion drift, the electric field E is eastward, the neutral wind u_n is equatorward, and the gravitational acceleration g is downward (Schunk 1988; Jee 2005; Schunk & Nagy 2009).

Fig. 1. Vertical components of the plasma drifts by an electric field (E), neutral wind (u_n), and vertical forces (F) from left to right. The angle I is the inclination of the geomagnetic field B.

Download Original Figure

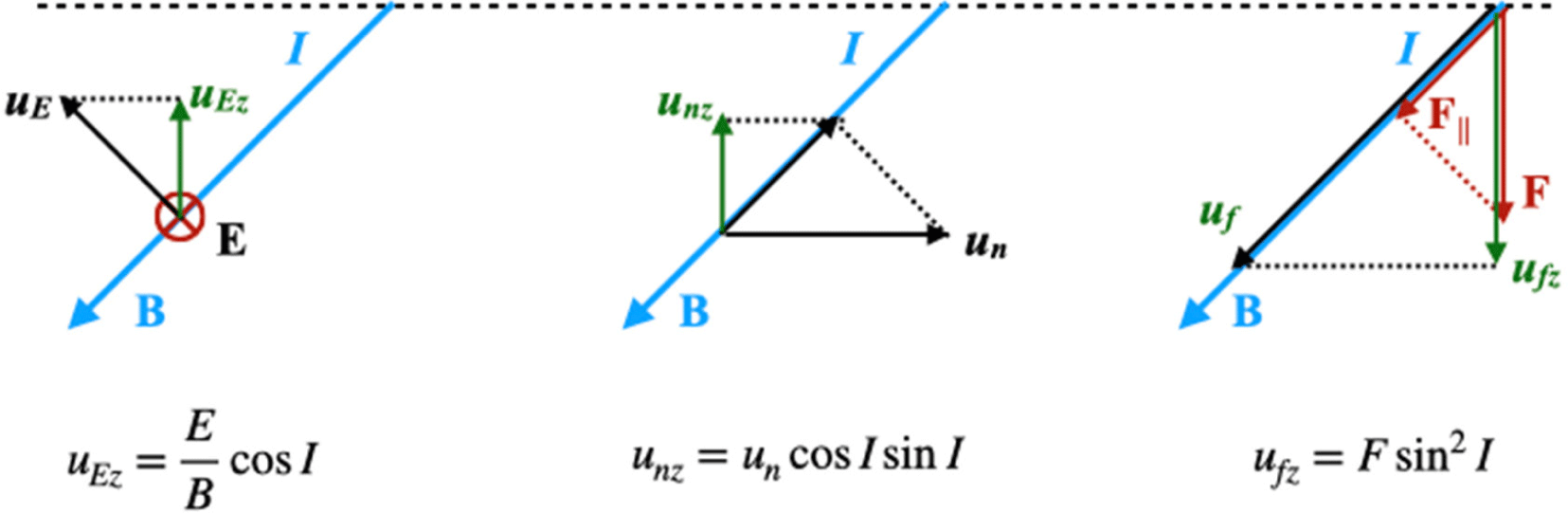
The diffusion Eq. (7) can be utilized to derive the partial differential equation for the major ion (O⁺) density by substituting the equation into the continuity Eq. (2). The resulting partial differential equation takes the form

where

To solve this partial differential Eq. (8), an initial density distribution and two boundary conditions are required for the first-order derivative in time and the second-order derivative in space, respectively. The initial density distribution can be obtained by assuming an arbitrary initial density profile and then computing a noon steady state distribution. This noon steady state density profile is subsequently used as the initial value for the calculation of diurnal variations of the density. At the lower boundary (z_b), diffusion is negligibly small and the ion density can be obtained by equating production and loss rates under the photo-chemical equilibrium condition

At the upper boundary (z_t), the O⁺ ions are in chemical equilibrium with H⁺ ions. In the topside ionosphere, the dominant ion is O⁺ and it extends from about 500 to 1,500 km at mid-latitudes. Above this region, there is a plasmasphere where H⁺ ions become dominant. In between the ionosphere and the plasmasphere, the O⁺ and H⁺ densities are controlled by the resonant charge exchange reaction

where k_f and k_r are the forward and reverse reaction rates which are the functions of ion and neutral temperatures and field-aligned velocities of the ions (Schunk & Nagy 2009). When the ionosphere and the plasmasphere are in equilibrium, diffusive equilibrium prevails, which allows a flow of ions between the two regions. The flow is upward from the ionosphere during the day, when the O⁺ density is relatively high, and downward at night, when the O⁺ density decays. The downflowing H⁺ ions undergo a resonant charge exchange reaction with O to produce O⁺, and this process helps to maintain the nighttime F region. The upflowing O⁺ ions also are converted to produce H⁺ by the resonant charge exchange reaction with H, which fills the flux tube in the plasmasphere. The direction of the plasma flux, upward or downward, is determined by relative differences of temperature, density and pressure in the ionosphere and the plasmasphere, which varies with day and night, season, solar cycle, and geomagnetic activity (Jee et al. 2005). The so-called plasmaspheric flux can be obtained by integrating the continuity equation for O⁺ from the upper boundary (z_t) to infinity

where the loss term is negligible in this high-altitude range. The production rate for O⁺, at the altitude well above the peak production, can be expressed as

where H_o = kT_n / m_og is the scale height for neutral atomic oxygen O, and P'_i is the O⁺ ionization rate per neutral particle at the top of the atmosphere, and the O⁺ density is assumed to follow diffusive equilibrium profile

where H_o⁺ = 2kT_p / m_o⁺g is the scale height for O⁺_. The resulting O⁺ flux at the upper boundary (z_t) is

where the first term on the right-hand side (${\left[n_i{u}_i\right]}_{\infty }$) corresponds to the O⁺ flux that escapes from, or enters, the upper boundary of the ionosphere.

The H⁺ density in the topside ionosphere can also be determined by using the resonant charge exchange reaction (14). When the H⁺ is in chemical equilibrium with O⁺, largely in the topside ionosphere, the H⁺ density is smaller than the O⁺ density and their density is controlled by the charge exchange reaction (14). Then the H⁺ density under the chemical equilibrium condition can be obtained as

where the ion and neutral temperatures are assumed to be relatively high and comparable each other, and the field-aligned velocity is negligible in the chemical equilibrium condition. When the diffusive equilibrium prevails and the H⁺ density becomes larger than the O⁺ density, it decreases exponentially with altitude

where z₀ is the altitude when $n_{O^{+}}=n_{H^{+}}\text{ and }{H}_{H^{+}}=2k{T}_p/m_{H^{+}}g$.

5. NUMERICAL SOLUTION

The derivatives in the differential Eq. (8) can be differenced as follows

where $z=j\Delta z=jh,t=i\Delta t=ik,A_j\left(z\right)=A_j\left(jh\right)$, and the fully implicit method was taken for the derivative terms (θ = 1) (Press et al. 1992). The differences of the derivatives convert the partial differential Eq. (8) into a set of linear algebraic equations and form a tridiagonal system, which can be solved at each time step by standard tridiagonal matrix techniques. The linear algebraic equations are

where

and j = 2, 3, …, J – 1.

Using the boundary conditions at the lower and upper boundaries, the algebraic Eq. (25) can be expressed in the following way. At the lower boundary point (j = 1), the algebraic equation becomes

where n₀ is the O⁺ density at the lower boundary, which is defined by Eq. (13). For the algebraic equation at the upper boundary point (j = J), one can use the differenced form of the flux, ${\left(nu\right)}_{{}^j}^i$

where the E × B drift term in Eq. (7) is neglected, v is the horizontal neutral wind, D_a is the ambipolar diffusion coefficient and Q is defined as

When Eq. (31) is rearranged and applied at the upper boundary, one can obtain

where (nu)_J is the upper boundary flux, which is defined by Eq. (18). Then Eq. (25) at the upper boundary (j = J) becomes

The linear algebraic Eq. (25) then can be easily solved numerically with the lower and upper boundary conditions described above to produce the vertical profile of the ionospheric electron density in the specified temporal resolution.

6. SUMMARY AND CONCLUSION

This review briefly introduced three types of approach to the ionospheric modelling, including an empirical model, a physics-based model, and a physics-based data assimilation model with models recently available for research community. Among the three types of modelling approaches, the physics-based model has a fundamental importance not only for better understanding of physical processes occurring in the ionosphere but also for the specifications and forecasts of the state of the ionosphere which will be a key component of space weather forecast model. Therefore, the simplified but fundamental equations for the mid-latitude ionospheric model and their numerical solutions were described with required boundary conditions for the lower and upper boundaries of the ionosphere.