1. INTRODUCTION
The present study investigated the chemical composition of HD47536 in detail and analyzed specific chemical abundance features observed in similar stars. HD47536 is a bright (V = 5.25) halo or an intermediate-population K-type giant. Different investigators have determined that the iron abundance in HD47536 ranges from [Fe/H] = –0.54 ± 0.10 (Sadakane et al. 2005) to [Fe/H] = –0.68 (da Silva et al. 2006).
It hosts one or two planets, of which the first was discovered by Setiawan et al. (2003). The mass of this planet can be more than 4.0 ± 0.4 times that of Jupiter, the semimajor axis of its orbit is 1.12 ± 0.005 astronomical units, and the eccentricity of its orbit is 0.3 ± 0.1 (Soto et al. 2015). Notably, the radius of the star is 21.36 ± 1.47 R⊙ (van Belle & von Braun 2009). This means that the shortest distance between the planet and the host star can be as small as 0.78 astronomical units, or near eight radii of the host star. Soto et al. (2015) examined the existence of a second planet.
Importantly, only 42 halo or thick disk stars are known as planetary hosts (Perottoni et al. 2021), and HD47536 is one of the brightest.
Numerous studies have compared the chemical abundances of stars with and without planets. The survey of 1111 FGK stars by Adibekyan et al. (2012) revealed that for stars with giant planets up to 0.5 dex, the abundances of N, Mg, Al, Si, Ca, and iron peak elements were higher than for stars without planets or those with Neptunian and super-Earth planets.
The chemical composition of HD47536 has been previously analyzed. Metallicity (Sadakane et al. 2005) and the abundance of a few chemical elements, specifically the upper limits of lithium and beryllium, were determined by Gálvez-Ortiz et al. (2011). The abundance of oxygen was determined by Ecuvillon et al. (2006); sodium, magnesium, and aluminum by Beirão et al. (2005); sulfur by Caffau et al. (2005); and Si, Ca, Sc, Ti, V, Cr, Mn, Co, and Ni by Gilli et al. (2006). The star was also included in the Luck (2015) Survey.
The preliminary abundance distribution in HD47536 was determined by Yushchenko et al. (2013), who derived the abundances of 33 chemical elements using the model atmosphere method. These results were used as the basis for calculating the individual atmospheric model using the ATLAS12 code.
The second and third sections of this paper describe the observations, data reduction, and model atmospheric parameters of HD47536. In the fourth section, we report the abundances of 38 chemical elements in the atmosphere of HD47536 derived using the differential spectrum synthesis method.
In the last section of the paper, we discuss the obtained results and outline possible ways to develop a theoretical explanation regarding the observed correlations of the abundances of chemical elements in the atmosphere of HD47536 with condensation temperatures and second ionization potentials of the elements.
2. OBSERVATIONS AND DATA REDUCTION
Four spectra of HD47536 were obtained using the Chiron spectrograph installed on a 1.5 meter SMART Cerro Tololo Inter-American Observator (CTIO) telescope (Chile) in 2012. These spectra were observed at heliocentric Julian dates 2,444,897.834, 2,444,897.835, 2,444,900.781, and 2,444,900.746 with exposure times of 50, 50, 300, and 600 s, respectively. The 3-pixel sampling spectral resolving power was R = 30,000, the wavelength range was 4,105–8,170 angstroms, and the signal-to-noise ratio S/N at the centers of echelle orders in the red part of the wavelength region exceeded 100 and 250, respectively, for the first two and the last two spectra.
The initial reduction of spectra was performed using the standard Image Reduction and Analysis Facility (IRAF) package, whereas the final processing of spectra, including continuum placement, co-adding of the spectra, identification of spectral lines, and equivalent width measurements, was performed using the latest version of the URAN code (Yushchenko 1997).
We found no significant differences between the observed spectra; therefore, all measurements were performed using the average observed spectrum of the star. The four observed spectra were shifted in accordance with radial velocity corrections and were co-added with weights proportional to exposure times.
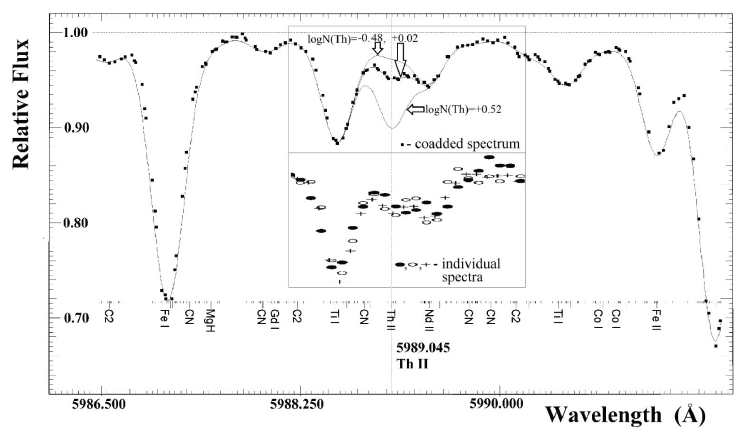
An example of the spectrum in the vicinity of the thorium line 5,989.045 Å is shown in Fig. 1, which shows the averaged profile over the four observed spectra compared to the synthetic spectrum. The synthetic spectrum of HD47536 was calculated for the entire observed wavelength region using the Kurucz (1993) SYNTHE code. This was considered when placing the continuum and identifying spectral lines.
3. ATMOSPHERIC PARAMETERS OF HD47536
The atmospheric parameters derived by Yushchenko et al. (2013) (Teff = 4,400K, log g = 1.80, vmicro = 1.5 km/s) and the abundances of chemical elements were used as input information for calculating the individual atmosphere model with the ATLAS12 code (Kurucz 1993). To test the accuracy of this model, we calculated the correlation coefficients of iron abundance determined using the Kurucz’s (1993) WIDTH9 code for 90 lines of neutral iron as a function of log (Eq. width/λ) and the excitation potential of the lower level for these lines. They were determined to be equal to 0.00 ± 0.11 and 0.07 ± 0.11, respectively. The value of the microturbulent velocity used for these calculations was slightly changed: vmicro = 1.44 km/s.
The abundance of iron derived from 90 lines of neutral iron and 18 lines of ionized iron were determined to be equal to log N(Fe) = 6.99 ± 0.11 and log N(Fe) = 7.01 ± 0.15, respectively. The oscillator strengths for lines of neutral and ionized iron were taken primarily from Fuhr & Wiese (2006) –73 lines, for 25 lines Kurucz (1993) values were used, and for 10 lines, we calculated the solar oscillator strength.
The above correlations and abundances of iron derived from neutral and ionized iron lines implied that the ATLAS12 model could be used to determine the abundances of all chemical elements using the spectrum synthesis method. To estimate the influence of possible uncertainties in atmospheric parameters on the derived abundances, we calculated two additional atmospheric models with slightly shifted parameters, specifically the effective temperature increased by 100K and the surface gravity increased by 0.4 dex. All calculations were made for these three atmosphere models as well as for the first model with the microturbulent velocity increased by 0.1 km/s. The spectral synthesis method was extremely sensitive to the observed spectral line profiles. Therefore, special attention was paid while determining the broadening parameters. First, we found that the spectral resolving power at the time of observation was higher than that described in the previous section. Based on terrestrial line profiles, we estimated the spectral resolution to be R = 48,000. Subsequently, the additional line broadening in the spectrum of HD47536 was approximated by the macroturbulent velocity vmacro = 7 km/s. The broadening of the observed spectrum by the rotational profile was neglected.
Notably, the difference between the standard resolving power of the spectrograph and the value obtained from our observed spectra can be explained by better assessment at the moments of our observations, primarily by different methods of deriving the resolving power in our investigation. The value of 3-pixel sampling spectral resolution is strongly dependent on the charge-coupled device used; however, the value of the instrumental profile of the spectral optical system used can be different.
4. CHEMICAL COMPOSITION OF HD47536
The atmospheric parameters described in the previous section were used to calculate the synthetic spectrum of HD47536 over the entire observation region. A comparison of this spectrum with the observed spectra of HD47536 made it possible to reliably identify the spectral lines and select the best lines for determining the chemical composition. The abundances of all chemical elements (except iron) in the HD47536 atmosphere were derived using the spectrum synthesis method. We used Kurucz’s (1993) SYNTHE code and our URAN (Yushchenko 1997) software to perform calculations in semiautomatic mode.
We managed to find the counterparts of most lines in the solar spectrum. Furthermore, the abundances of the solar lines were derived using the spectrum synthesis method. We used the Liége solar atlas (Delbouille et al. 1973) and the Grevesse & Sauval (1999) solar atmosphere models. The adopted values of microturbulent and macroturbulent velocities for this model were 0.8 km/s and 1.8 km/s, respectively. The continuum level in the solar spectrum was adjusted according to Ardeberg & Virderfors (1979) and Rutten & van der Zalm (1984). The same codes were used to build a synthetic spectrum, identify lines, and determine the abundances.
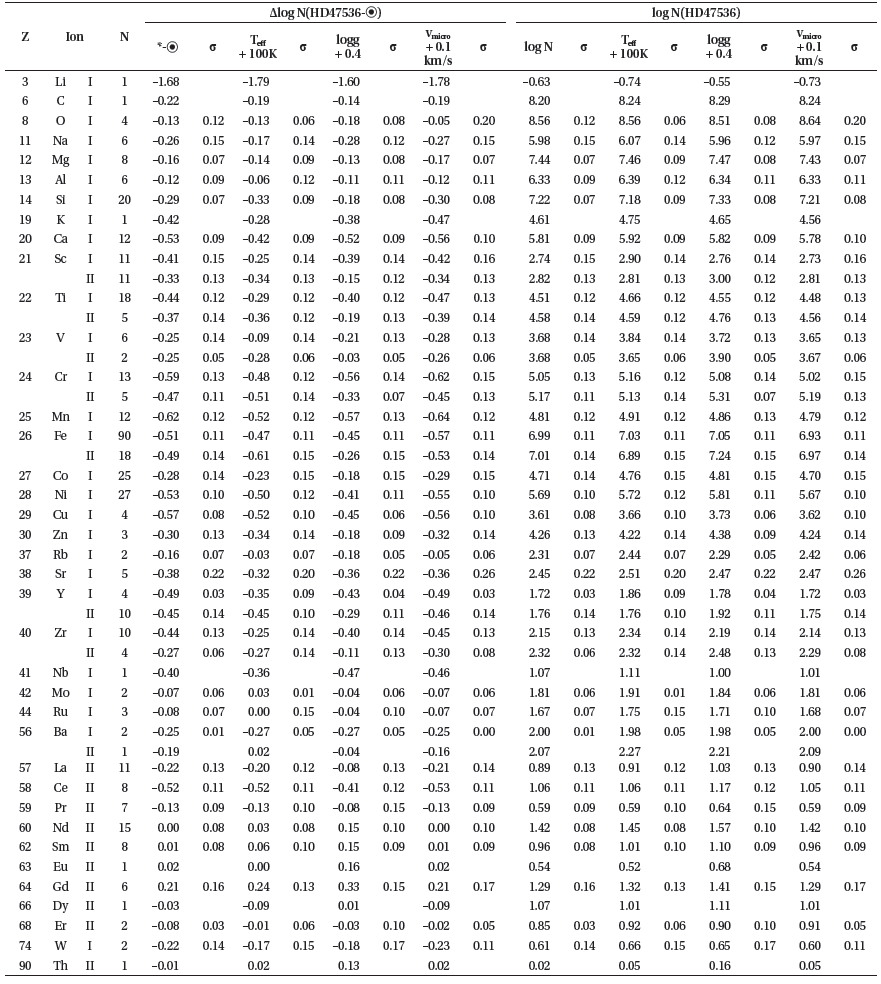
Table 1 presents the average relative and absolute values of abundances in the atmosphere of HD47536 for 38 chemical elements. The first two columns indicate atomic numbers and ion identification. The third column lists the number of lines used. The two subsequent groups of columns present the mean abundances in the atmosphere of HD47536 and their errors for the four sets of atmospheric parameters, specifically for the best values and for effective temperature, surface gravity, and microturbulent velocity increased by 100K, 0.4 dex, and 0.1 km/s, respectively. The first and second groups of columns depict relative and absolute abundances, respectively. The relative abundances (*–⊙) and the absolute abundances (log N) in the atmosphere of HD47536 are the first columns of each group.
|
Fig. 2 shows the relative abundances of chemical elements in the atmosphere of HD47536 as a function of the atomic number.
5. DISCUSSION
From Table 1 and Fig. 2, we can conclude that there is a well-expressed regularity in the [El/Fe] distribution. The light elements (from carbon to silicon) appear to be slightly overabundant, the iron-peak elements are deficient (being nearly at the same level of iron abundance), and the scenario for heavier species is rather controversial. Some elements are more abundant than iron (e.g., Rb, Mo, Ru, Ba, Sm, Eu, and others), while others are equally abundant (e.g., Y, Zr, and Ce).
In Fig. 3, we depict the abundances in HD47536 superimposed on the scaled abundances of the solar system r-process elements. The deviations from the distribution of the solar r-process elements were fitted by the s-processes for Ba, Nd, and heavier lanthanides. The abundances of light lanthanides, La (Z = 57), Ce (58), and Pr (59), decreased with respect to the s-process enrichment of the solar system.
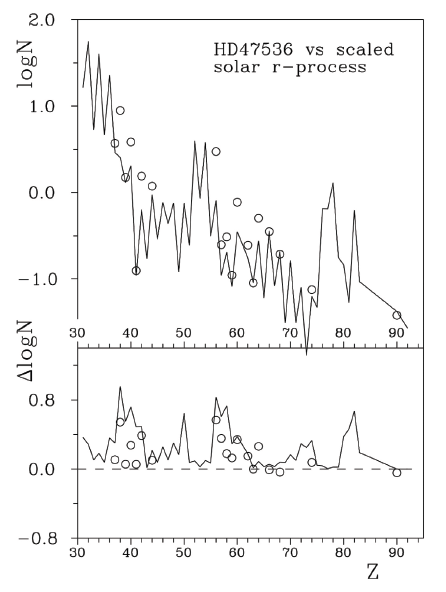
A possible reason for this decrease can be attributed to charge-exchange reactions. We describe this in more detail in this section. The abundances of elements with atomic numbers of 37 ≤ Z ≤ 42 can be explained by the s-process enrichment only for Sr (38), Zr (40), and Mo (42). The abundances of Rb (37), Y (39), and Nb (41) were not strongly influenced by the s-process.
We investigated whether it is possible to explain the different behaviors of the two groups of chemical elements with odd and even atomic numbers and whether it is sufficient to have only information regarding nuclear processes from previous stellar generations. To make the situation more understandable, it is necessary to examine the relationship between the abundance of the studied chemical elements and some of their physical properties. Among these are properties such as the second ionization potential (SIP) and condensation temperature.
These two characteristics may be important when considering the possible observational manifestation of such chemodynamical processes, such as interaction between atoms in the stellar atmosphere and interaction of the stellar atmosphere with circumstellar or interstellar media. Figs. 4 and 5 show the derived elemental abundances in our program stars depending on the SIP and condensation temperature of the studied chemical elements. The relationships obtained are discussed below.
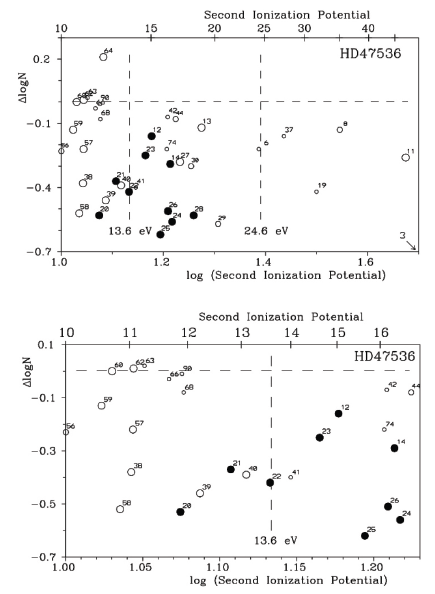
Greenstein (1949) was the first to reveal that in some metallic-line stars, the abundances of elements such as Na, Mg, Al, Si, Sc, Ti, V, and Zr are reduced. He supposed that these elements can persist in the second ionization stage, and therefore, the corresponding lines are not seen in the visual part of the spectra of A–F stars. This mechanism is possible in a non-equilibrium medium if the SIPs are close to the hydrogen ionization potential.
In such a case, the overionization of hydrogen may cause an excess of the above-mentioned elements in the second ionization stage and the respective reduction of their abundances derived from the lines of neutral and first ionization species. This can be achieved either due to the UV line and continuous emission of hydrogen or due to the charge-exchange reactions between ionized hydrogen and the mentioned atoms in the first ionization stage.
Charge-exchange reactions are possible in the case of resonance between the hydrogen ionization potential and SIP of certain chemical elements. Böhm-Vitense (2006) and Yushchenko et al. (2015) observed the same effect for helium, specifically the decrease of relative abundances for chemical elements with SIPs close to or greater than SIP = 24.6 eV.
The value of helium’s first ionization potential is 24.6 eV. Havnes (1971) and Havnes & Conti (1971) suggested that the chemical peculiarity of magnetic stars can be caused by the selective capture of atoms from the ionized interstellar medium. If such a mechanism is implemented to explain some chemical anomalies in HD47536, then we need to suppose that this star was a mid- to late-type dwarf at the main sequence with a rather strong magnetic field.
The charged atoms with a smaller charge-to-mass ratio easily penetrate the main sequence star magnetosphere and reach the stellar atmosphere, whereas the lighter species are reflected in the zones of locally increased magnetic field. In principle, such a mechanism can also work in the circumstellar envelope, possibly with a higher efficiency, because the expected gas concentration in the circumstellar envelope should be much higher than that in the interstellar medium. SIPs for Sr and Zr are close to the ionization potential of hydrogen, while rare Earth’s have smaller SIPs (as a rule, lower than 12 eV), which may explain their increased abundance in the HD47536 star (Fig. 4). However, it should be noted that Borra & Landstreet (1980) did not succeed in detecting strong magnetic fields in metallic stars. North (1984) also doubts the validity of the findings of Havnes (1971) and Havnes & Conti (1971).
Importantly, Greenstein (1949) discovered the observation phenomenon, specifically the deficiency of relative abundances of chemical elements with SIPs between 12 and 16 eV and proposed an explanation for this phenomenon. His physical scenario did not require a magnetic field. Havnes (1971) and Havnes & Conti (1971) tried to develop Greenstein’s scenario for stars with strong magnetic fields; however, their hypothesis faced major problems and needed improvement.
Böhm-Vitense (2006) comprehensively discussed several possible scenarios regarding the formation of metallic-line stars. She came to a conclusion that only the charge-exchange mechanism is able to explain observed abundance peculiarities, particularly the deficiency of the chemical elements with SIPs that are close to 13.6 eV (hydrogen ionization potential) and 24.6 eV (helium first ionization potential).
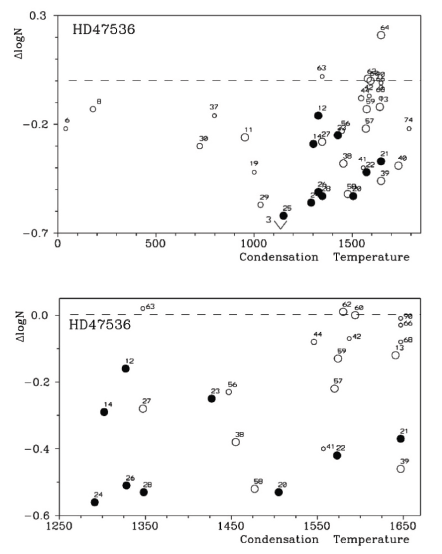
Here, we focus on Fig. 5, which shows the relative abundances of 38 chemical elements as a function of their condensation temperature. We note that elements with condensation temperatures below 1,200–1,400K apparently show progressively decreasing abundance with respect to iron. The higher the condensation temperature, the lower the abundance. The lowest abundances in this group of elements were iron-peak elements (refractory siderophyles: Cr, Mn, Fe, and Ni; see Fig. 5).
After this minimum, elements with a higher condensation temperature showed an increased abundance. Among these elements, there are many whose abundances were derived using one or two lines and cannot be considered very reliable. A similar excess was observed for refractory lithophile elements such as Mg and Si, whose abundances were derived using a statistically significant number of lines. Notably, their abundances were higher than those of the iron peak elements, although their condensation temperatures were almost the same as that of iron. It is also interesting to note that the four elements: Na, K, Zn, and Rb, which are classified as volatile lithophile elements, showed a fairly close abundance in HD47536.
First, we discuss the behavior of elements with condensation temperatures below 1,400K, including refractory siderophile elements. This behavior resembles that observed in λ Bootype stars. The chemical peculiarities of λ Boo-type stars are due to a specific mechanism of contamination of their atmospheres by material from the circumstellar envelope, which has previously experienced dust and gas separation. In a certain temperature regime, the gaseous component around the central star consists of volatile fractions with low condensation temperatures and refractory elements with high condensation temperatures. These refractory elements can form dust particles even in a high-temperature environment.
Gravitational attraction acts with equal efficiency on the gas and dust components; however, the radiative pressure of the central star more efficiently removes dust particles farther from the star. Over time, this process reduces the fraction of refractory elements in the surroundings nearest to the star. While the gas component returns to the stellar atmosphere, some elements enclosed in the dust grains are lost to the stellar atmosphere. Thus, as a result, the stellar atmosphere acquires a specific chemical composition. It is not uncommon that dust grains containing refractory elements may coagulate at a greater distance from the star, forming planetesimals and subsequently, planet-like bodies. Recall that the star in our program HD47536 has at least one planet. Thus, mid- and late-type main sequence stars with planets may be deficient in refractory elements.
This scenario was first qualitatively proposed by Venn & Lambert (1990) and later investigated by Charbonneau (1991, 1993), Stuerenburg (1993), Andrievsky (1997), Andrievsky & Paunzen (2000), Andrievsky (2006), and Venn & Lambert (2008). λ Boo-type stars are the main sequence of A–F dwarfs, whose atmospheres are rather stable against convection. This convection may erase any signs of chemical peculiarity at the stellar surface layers, because a nonmodified stellar gas from the stellar interior is brought to the surface and mixed with a modified gas.
According to Jofré et al. (2015), HD47536 has a mass of approximately 0.9 solar masses; hence, on the main sequence it was a G, or possibly a late F dwarf (if some mass was lost during expansion). Therefore, HD47536 may be a borderline case between λ Boo- and non-λ Boo-type stars. Moreover, even for G main-sequence stars, a mechanism of dust-gas separation in the circumstellar medium is possible. Meléndez et al. (2009) reported that according to the LTE analysis of high-quality spectral material obtained for solar twin stars, our Sun has a small deficiency of refractory elements compared to the average solar twin abundances, which may be an indication of the loss of refractory elements from the proto-Sun owing to terrestrial-like planet formation from this lost material. This conclusion was based on the dependence of the relative abundances on the condensation temperature.
A similar conclusion was drawn by Ramírez et al. (2009) for a large sample of solar twins. These published results suggest that (if the described scenario is correct) the Sun has a somewhat unusual composition of refractory elements, as such a feature is not observed on average for the solar twins. It is possible to estimate the distance from the central star at which the temperature is close to the condensation temperature of siderophile refractory elements, such as Cr, Mn, Fe, and Ni (Tcond ≈ 1,300K). For this, we use the dilution factor W = 0.5 · (1 – (1 – (r*/r)2)0.5), where r* is the radius of the central (main sequence) star. For the effective temperature of the star, that is 6,000K, we assume that the required temperature of 1,300K takes place at approximately R equals to ten stellar radii, where the formation of the terrestrial-like planets can take place. As pointed out earlier, the planet of the HD47536 system approached the main star at a distance of approximately eight radii from the red giant star.
The abundance distribution of the high condensation temperature elements (> 1,300K) resembles that observed in the solar system chondrites (see Wood et al. 2019; Fig. 4). Therefore, the relative iron abundances of the lithophile refractory elements (Mg, Al, Si, Sc, Sr, Zr, Ni, and Ba, as well as all the studied rare earth elements and thorium) had positive values (see Fig. 5). We can conclude that the observed peculiarity of the chemical element distribution in the K-giant halo star HD47536 does not contradict the suggestion that it was formed under certain conditions connected with the dust-gas separation in the pristine envelope surrounding the central proto-star. It is also possible to conclude that the processes of star formation are pertinent to those that have taken place in the primitive solar system.
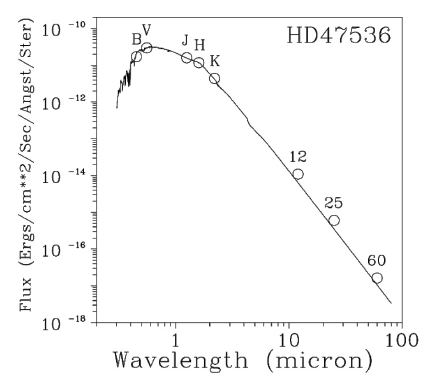
Additional evidence that HD47536 has signs of remnant circumstellar shells is its detectable IRAS flux. Fig. 6 shows the fit of the broadband photometry and IRAS fluxes for our program star using the theoretical fluxes calculated by Kurucz (1993).
As revealed by Greenstein (1949), the deficiency of relative abundances is observed for elements with SIP between 11.8 and 16 eV; therefore, it was concluded that resonance can be observed at the eV. Yushchenko et al. (2015) showed that the plot of relative abundances vs. SIPs for ρ Pup is a sawtooth graphic with two cutoffs near the values of SIP = 12 eV and SIP = 24 eV (Fig. 6 in Yushchenko et al. 2015). The sawtooth shape was also found for the main component of RR Lyn, as illustrated in Fig. 3 by Jeong et al. (2017), and for barium star ζ Cyg (Fig. 1 in Jeong et al. 2018).
For the abundance pattern of halo giant HD47536, the sawtooth picture was observed only for elements with SIPs of less than approximately 20 eV. The elements with higher SIP values in the sawtooth shape of relative abundances vs. SIP plots are not clearly visible. This may be explained by the lower density of the halo interstellar medium.
The chemical elements with SIPs between the two cutoffs, as well as the elements with SIPs less than the first cutoff and greater than the second cutoff, show positive correlations of relative abundances vs. SIPs in the above-mentioned three stars. Yushchenko et al. (2015) and Yushchenko et al. (2021) found similar correlations in the published observations of several hundred B–F type stars and disk red giants for chemical elements with SIPs between the two cutoffs and greater than the second cutoff. It was also shown that these correlations are dependent on the effective temperature and disappear for stars with convective energy transfer in their atmospheres. Note that not all relative abundances of chemical elements between the cutoffs followed the described sawtooth shape in the relative abundances vs. SIPs plots.
A portion of the elements showed higher relative abundance. In the case of ρ Pup, these are Mo (Z = 42), Ru (44), Cd (48), and elements with atomic numbers Z ≥ 71, namely Lu, Hf, Os, Ir, Pt, Au, and Pb. In the atmosphere of the primary component of RR Lyn, Lu, in the atmosphere of barium star ζ Cyg, an increase in relative abundance was observed for Mg (12), Nb (41), Mo (42), Ru (44), Pd (46), Hf (72), and Os (76). It is natural to expect that several physical scenarios occur in the atmosphere of certain stars, and the relative abundances of the above-mentioned chemical elements are influenced not only by charge-exchange reactions but also by other scenarios.
Let us return to the chemical elements with 37 ≤ Z ≤ 42 in the atmosphere of HD47536 and attempt to understand the low deviations of Rb (37), Y (39), and Nb (41) from the scaled solar system r-process izotopes fit (see Fig. 3). The SIPs of these elements were 27.29, 12.22, and 14.00 eV, respectively. This allows Rb, Y, and Nb to be influenced by charge exchange reactions, and we can expect a decrease in the relative abundance of these chemical elements with respect to s-process predictions. This is illustrated in Fig. 3. Rb has condensation Tcond = 798K, and its abundance can also be decreased owing to the dust-gas separation scenario. Sr (38) and Mo (42) had SIPs 11.03 of 16.16 eV, respectively. These values are outside the resonance region in the relative abundance vs. SIPs plots. Therefore, the relative abundances of these two chemical elements should not be strongly decreased by charge-exchange reactions, and s-process enrichment can be detected, as shown in Fig. 3.
Zr (40) has an SIP of 13.1 eV and should be influenced by charge-exchange reactions; however, Fig. 3 shows significant enrichment by the s-process. At present, we are not able to explain the abundance of this element; perhaps, additional physical effects, such as example dust-gas separation, radiative diffusion in stellar atmospheres, or other scenarios should be taken into account.
Similar considerations can be made for lanthanides. Fig. 3 shows that the first three lanthanides, La, Ce, and Pr are underabundant with respect to the solar system s-process curve. The SIPs of these three chemical elements are 11.05, 10.85, and 10.55 eV, respectively, while the SIPs of other six lanthanides investigated in the atmosphere of HD47536, specifically Nd, Sm, Eu, Gd, Dy, and Er, are from 10.72 eV for Nd to 11.07 eV for Sm and higher values for the other four elements. The highest SIPs among the investigated lanthanides were 12.09 eV for Gd.
We can conclude that the three lanthanides with the lowest SIPs exhibit negative deviations from the solar system s-process approximation. For the other six lanthanides with higher SIPs, the fit of their abundances by the solar system s-process distribution results in close to zero or positive (for Gd) deviations.
Fig. 4 shows the positive correlations between the relative abundances of lanthanides and SIPs. This allows us to suppose that the abundances of lanthanides varied owing to charge-exchange reactions, and we should detect a decrease in relative abundance for lanthanides, with the lowest SIP values. The observed relative abundances show negative deviations from the solar system s-process fit for the first three lanthanides with the lowest SIPs, close to zero deviations for the other lanthanides, and the element with the highest SIP – for Gd.
In summary, the solar system s-process isotope abundance distribution fits the observed relative abundances in the atmosphere of HD47536. Negative deviations are observed for Rb (37), Y (39), Nb (41), La (57), Ce (58), and Pr (59). The abundances of these six chemical elements can be influenced by charge exchange reactions, and we should expect a decrease in the relative abundances of these elements over time.
Note that the SIP for Th is 11.9 eV, and the abundance of this radioactive element can be changed not only because of the natural radioactive decay but also because of chargeexchange reactions. The SIP for Th was in the first highest region of the sawtooth picture observed in the plot of relative abundances against SIPs. Therefore, we can expect that the influence of charge-exchange reactions on thorium abundance is relatively weak with respect to the abundance of other chemical elements; however, this conclusion is qualitative and requires additional investigation.
6. CONCLUSION
The chemical composition of the planetary host halo star HD47536 was investigated. The abundances of 38 chemical elements were determined using the spectrum synthesis method. It was shown that the abundance pattern of this star is influenced by r- and s-process enrichment, chargeexchange reactions, and dust-gas separation. The interplay of these three scenarios allows us to qualitatively explain the atmospheric abundances of this star.
Our results obtained for HD47536 and other stars indicate that the plot of relative abundances of chemical elements vs. SIPs of these elements can be a sawtooth picture with two cutoffs, with SIPs near 12 or 13 eV and near 24 eV. The relative abundances of chemical elements with SIPs in three intervals, namely SIP < 12 eV, 12.5 eV < SIP < 20 eV, and SIP > 24.6 eV show the positive correlation with respect to SIP.
In summary, one can conclude that both the dust-gas separation mechanism and charge-exchange reactions discussed above can be involved in the interaction between the star’s atmosphere and circumstellar/interstellar medium; this interaction produces a specific abundance pattern, which is observed in our program star HD47536 as well as in other stars.
Note that the dependence of relative abundances on SIPs was discovered by Greenstein (1949) as soon as the use of high dispersion spectra and quantitative analysis of stellar abundances allowed for the first stellar abundance patterns. However, the explanation for this dependence remains qualitative.
It should be mentioned that Jeong et al. (2018) found the possibility of age dependence for correlations of relative abundances vs. SIPs in barium stars. This means that the abundance of stable (non-radioactive) chemical elements in stellar atmospheres varies with time. If this possibility is confirmed for other types of stars, it would be difficult to use Th/Eu or other radioactive to stable element abundance ratios to determine the age of the star. We found both Th and Eu abundances in the atmosphere of halo giant HD47536. We also found a clear dependence of lanthanide abundance on the SIP (see Fig. 4). The SIP of thorium is 11.9 eV, which is similar to that of lanthanides. It seems natural to expect that Eu and Th atoms in the atmosphere of HD47536 can be influenced by charge-exchange reactions owing to accretion of interstellar matter, and the abundance ratio of these elements can change with time owing to the natural radioactive decay of Th atoms. Therefore, we did not attempt to estimate the age of HD47536 by using the Th/Eu abundance ratio.
A detailed analysis of the correlations between the relative abundances against second ionization potentials and condensation temperatures found in this study is the addition of previous determinations of these values for different types of stars and will be used for constructing the quantitative theory of charge-exchange reactions in stellar atmospheres.