Journal of Astronomy and Space Sciences

The Korean Space Science Society

2021; 38(3):185-192

pISSN: 2093-5587, eISSN: 2093-1409

DOI: https://doi.org/10.5140/JASS.2021.38.3.185

Technical Paper

Practical Algorithms on Lunar Reference Frame Transformations for Korea Pathfinder Lunar Orbiter Flight Operation

Young-Joo Song1

, Donghun Lee2^,†

, Young-Rok Kim1

, Jonghee Bae1

, Jae-ik Park1

, SeungBum Hong1

, Dae-Kwan Kim1

, Sang-Ryool Lee3

¹Lunar Exploration Program Office, Korea Aerospace Research Institute, Daejeon 34133, Korea

²School of Aerospace and Mechanical Engineering, Korea Aerospace University, Goyang 10540, Korea

³Director’s Office, Korea Aerospace Research Institute, Daejeon 34133, Korea

^†Corresponding Author Tel: +82-2-300-0105, E-mail: donghlee@kau.ac.kr

© The Korean Space Science Society. All rights reserved. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jun 16, 2021; Revised: Jul 13, 2021; Accepted: Jul 15, 2021

Abstract

This technical paper deals the practical transformation algorithms between several lunar reference frames which will be used for Korea pathfinder lunar orbiter (KPLO) flight operation. Despite of various lunar reference frame definitions already exist, use of a common transformation algorithm while establishing lunar reference frame is very important for all members related to KPLO mission. This is because use of slight different parameters during frame transformation may result significant misleading while reprocessing data based on KPLO flight dynamics. Therefore, details of practical transformation algorithms for the KPLO mission specific lunar reference frames is presented with step by step implementation procedures. Examples of transformation results are also presented to support KPLO flight dynamics data user community which is expected to give practical guidelines while post processing the data as their needs. With this technical paper, common understandings of reference frames that will be used throughout not only the KPLO flight operation but also science data reprocessing can be established. It is expected to eliminate, or at least minimize, unnecessary confusion among all of the KPLO mission members including: Korea Aerospace Research Institute (KARI), National Aeronautics and Space Administration (NASA) as well as other organizations participating in KPLO payload development and operation, or further lunar science community world-wide who are interested in KPLO science data post processing.

Keywords: lunar reference frame; practical transformation algorithm; Korea pathfinder lunar orbiter

1. INTRODUCTION

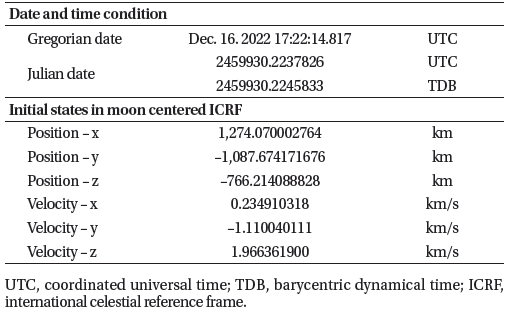
The Korea pathfinder lunar orbiter (KPLO) is the first space exploration mission of the Republic of Korea beyond the Earth orbit. KPLO will be launched using Space-X Falcon-9 launch vehicle, with expected launch period of around 40 days: from late July to early September 2022. Recently, transfer method to reach the Moon for KPLO have changed from 3.5 phasing loop to weak stability boundary (WSB) / ballistic lunar transfer (BLT) trajectory to secure more fuels to KPLO. After a long journey to the Moon, KPLO will arrive on the Moon around mid-December 2022 and nominal mission orbit will be established with several lunar orbit insertion (LOI) burns. The nominal mission orbit around the Moon will have 90 deg of inclination with an altitude of approximately 100 ± 30 km throughout the mission life, which will be about 12 months including the commissioning phase. Fig. 1 shows the WSB/BLT transfer trajectory during the launch period with respect to Earth- Sun rotating frame, shown left side of the figure, and lunar orbit acquisition (LOA) phase of the KPLO, shown in right side, respectively. In the left side of figure, the part where the color of the flight trajectory changes from red to blue is the point where the first deterministic delta-V is performed. The recent progress on various KPLO trajectory design and analysis can be found on Refs (Kim et al. 2019a, 2019b, 2020a, 2020b, 2020c, 2021;Bae et al. 2020a, 2020b, 2020c, 2021;Hong et al. 2020a, 2020b;Lee et al. 2020a, 2020b, 2020c;Park et al. 2020a, 2020b;Song et al. 2020a, 2020b).

Fig. 1. The WSB/BLT transfer trajectory during the launch period and LOA phase of the KPLO. WSB, weak stability boundary; BLT, ballistic lunar transfer; LOA, lunar orbit acquisition; KPLO, Korea pathfinder lunar orbiter.

Download Original Figure

Many collaborative efforts are currently being devoted for the successful launch and operation of KPLO lead by Korea Aerospace Research Institute (KARI) team. For the transfer trajectory design and Deep Space Network (DSN) activities, KARI is now working closely with National Aeronautics and Space Administration (NASA) Jet Propulsion Laboratory (JPL). With NASA Johnson Space Center (JSC), KARI is coworking for nominal mission orbit design as well as for further KPLO flight operation. Beside of NASA, there are numerous collaborators involved with KPLO mission with payload development and operation. The KPLO will carry six payloads to the Moon which include: LUnar Terrain Imager (LUTI), Polarimetric Camera (PolCam), KPLO Gamma Ray Spectrometer (KGRS), KPLO Magnetometer (KMAG), Disruption Tolerant Network (DTN) payload and finally, Shadow Camera (ShadowCam). Each of payloads is mainly being developed and associated operational concept is being established from KARI for LUTI, the Korea Astronomy and Space Science Institute (KASI) for PolCam, the Korea Institute of Geoscience and Mineral Resources (KIGAM) for KGRS, KyungHee University (KHU) for KMAG, the Electronics and Telecommunications Research Institute (ETRI) of Korea and NASA for DTN technologies demonstration, and Arizona State University (ASU) and Malin Space Science Systems (MSSS) for ShadowCam (Song et al. 2017).

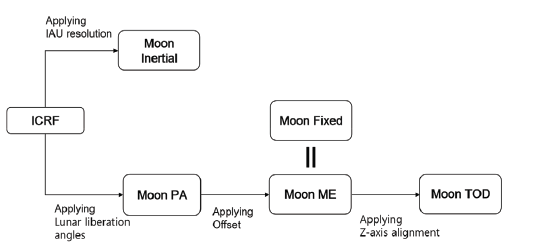
During phases of trajectory design, analysis, flight operation and science data pre- and post-processing, various different types of reference frames will properly be used to express KPLO flight trajectory or orbit data. Among several different mission phases, sharing common knowledge and background on frame transformation to be used from LOA to the end of nominal mission phases is especially important as many teams (mission engineers, planners, operator as well as scientists) are closely and directly involved for these mission phases. Such a clear definition as well as detailed transformation algorithms on the lunar reference frames for KPLO mission will make many team members to communicate clearly and effectively without any unnecessary debates which occasionally happens through ambiguous reference frames definitions and transformations. Indeed, many different definitions on lunar reference frame already exists (Roncoli 2005;LRO Project 2008), however, those of defined reference frames are likely to be slightly different dependent to the specific missions, i.e., sometimes same frame definitions with different names. In addition, it is very well known that the Navigation Ancillary Information Facility (NAIF) has built a data system called “SPICE” which intended to support the scientists while planning and postprocessing science data from the science payloads (NAIF 2021). Despite of well organized SPICE data system, it is still necessary to the community members to know the exact definition as well as the parameters used on frame transformations for the specific mission as to fully applicate SPICE data system.

The main purpose of this technical paper is to provide clear definitions on transformation of lunar reference frames that will be used for KPLO flight operation as well as science data post processing. Actually, there exist literatures that treated definition of lunar reference frames (Roncoli 2005;LRO Project 2008). Despite of various lunar reference frame definitions already exist, use of a common transformation algorithm while establishing lunar reference frame is very important as use of slight different parameters during frame transformation may result significant misleading while reprocessing the flight dynamics data. Therefore, current work is more focused on practical aspect of transformations on lunar reference frames that are specialized and utilized to release the KPLO fight dynamics data. Details of step by step transformation algorithms are presented in as much as detail as possible including example transformation results to support user community while reprocessing KPLO trajectory or orbit data as their needs. Cautionary points while implementing transformation procedures is also specified in detail as to support users to achieve the most precise results. In here, note that the most of the KPLO trajectory or orbit data will be generated from Flight Dynamics Subsystem (FDS) and provided through the Korea Planetary Data Subsystem (KPDS) which are the two of the subsystem consisting KPLO Deep space Ground System (KDGS). The remainder of this manuscript is organized as follows. Brief definition of each different lunar reference frames and practical transformation algorithms between those of coordinate system is provided in Section 2. Each different reference frames include: Moon Inertial, Moon principal axis (PA), Moon mean earth (ME) which is equivalent Moon Fixed, and Moon true of date (TOD). In Section 3, example transformation results are provided including cross-checked results against to the flight proven systems tool kit (STK) Astrogator’s results. Finally, the conclusions are presented in Section 4. Through this article, it is expected to give practical insights as well as guideline not only to the KPLO mission team members but also to the lunar science user community world-wide who are interested in the KPLO flight and science data post processing.

2. Lunar reference frames and transformation details

As discussed, the KPLO flight data as well as science data will be accessed, reproduced and processed from many different partners world-wide for the new science discovery. Therefore, the reference frames for the KPLO flight data have been chosen to be, as much as possible, to follow the existing lunar reference frame definitions (Roncoli 2005;LRO Project 2008) that is already defined based on the accomplishment of previous lunar missions world-wide. In Fig. 2, overview of lunar reference frame transformation flow for the KPLO flight data is presented. As easily expected, conversion to every defined lunar reference frame start from with respect to the international celestial reference frame (ICRF), and step by step sequential transformation algorithms are applied to form different target lunar reference frames. In following subsections, details on practical transformation sequences are treated for lunar reference frames other than ICRF, as readers may find numerous literatures treating details on ICRF. In addition, for more in-depth definitions on existing lunar reference frames, intentionally not treated in this work as to more focused on practical transformation algorithms, readers may refer Refs. Roncoli (2005) and LRO Project (2008).

Fig. 2. Overview of lunar reference frame transformation flow for the KPLO flight data. KPLO, Korea pathfinder lunar orbiter.

Download Original Figure

2.1 Moon Inertial Frame

The Moon inertial frame for the KPLO mission is defined to follow definition of the International Astronomical Union (IAU) working group (WG). It is well known that IAU WG on cartographic coordinates and rotational elements (CCRE) revises recommendations on the definition of reference frames for the planetary bodies almost every three years, and among various report they have provided, the KPLO utilized definitions in Ref. Archinal et al. (2011). The definition of the Moon Inertial frame can be initiated from the direction of the north pole of the Moon. In Ref. Archinal et al. (2011), the direction of the north pole of the Moon is specified by the value of its right ascension α₀ and declination δ₀ with respect to ICRF equatorial coordinates at epoch J2000.0 as in Eq. (1).

α 0 = 269.9949 + 0.0031 T − 3.8787 sin E 1 − 0.1204 sin E 2 + 0.0700 sin E 3 − 0.0172 sin E 4 + 0.0072 sin E 5 − 0.0052 sin E 7 + 0.0043 sin E 8

(1a)

δ 0 = 66.5392 + 0.0130 T + 1.5419 cos E 1 + 0.0239 cos E 2 − 0.0278 cos E 3 + 0.0068 cos E 4 − 0.0029 cos E 5 + 0.0009 cos E 6 + 0.0008 cos E 7 − 0.0009 cos E 8

(1b)

where T is interval in Julian centuries (of 36,525 days) from the standard epoch and arguments in Eq. (1) are as follows:

E 1 = 125.045 − 0.0529921 d E 2 = 250.089 − 0.1059842 d E 3 = 260.008 + 13.0120009 d E 4 = 176.625 + 13.3407154 d E 5 = 311.589 + 26.4057084 d E 6 = 134.963 + 13.0649930 d E 7 = 15.134 − 0.1589763 d E 8 = 25.053 + 12.9590088 d

(2)

In Eq. (2) d is interval in days from the standard epoch. In Eqs. (1) and (2), the standard epoch is JD 2451545.0, i.e. 2000 January 1 12 hours barycentric dynamical time (TDB). Note that the unit of all constants used in Eqs. (1) and (2) is deg. Using α₀ and δ₀, the Moon’s north pole vector can be determined:

p ¯ I N T = [cos α 0 cos δ 0 sin α 0 cos δ 0 sin δ 0]

(3)

where subscript INT indicate the Inertial. The unit vector of x-axis direction, $x ¯ I N T$ , of the Moon inertial frame can be obtained using $x ¯ I N T = z ¯ I C R F × p ¯ I N T / ‖ z ¯ I C R F × p ¯ I N T ‖$ , where $z ¯ I C R F = [0 0 1]$ . Similarly, the unit vector of y-axis direction, $y ¯ I N T$ , can be determined using $y ¯ I N T = p ¯ I N T × x ¯ I N T / ‖ p ¯ I N T × x ¯ I N T ‖$ . Finally, direction cosine matrix which transforms ICRF to Moon inertial frame, $D I C R F I N T$ , can be obtained as in Eq. (4).

D I C R F I N T = [x ¯ I N T y ¯ I N T p ¯ I N T]

(4)

Spacecraft’s states in ICRF frame can simply be transformed to the Moon inertial frame as in Eq. (5).

s I N T = T I C R F I N T s I C R F

(5)

where $T I C R F I N T$ is 6 by 6 state transformation matrix and s is 6 by 1 state vectors with position, r, and velocity, υ, defined as:

T I C R F I N T = (D I C R F I N T 0 0 D I C R F I N T)

(6a)

s I C R F = [r I C R F v I C R F] T

(6b)

In Eq. (6a), 0 is a null matrix of order 3 by 3 and while formulating $D I C R F I N T$ , readers may NOTE that epoch time should be the same as the standard epoch, namely, 2000 January 1 12 hours TDB, which will always result constant 3 by 3 $D I C R F I N T$ as following.

D I C R F I N T = [0.998496505205088 -0.0548154092680678 0.000000000000000 0.0499357293985326 0.909610125238044 0.412451018902689 -0.0226086714041825 -0.411830900942613 0.910979778593430]

(7)

2.2 Moon Principal Axis (PA) Frame

Before to discuss the Moon PA frame, readers should be familiar with the definition of a lunar body-fixed frames. It is very well known that there is two slightly different frame used to define a lunar body-fixed frames. The first one is called PA frame which is a body-fixed frame aligned with the principal axes of the Moon. Another definition of a body fixed frame is the ME frame which is based upon a mean direction to the Earth and a mean axis of rotation of the Moon (Archinal et al. 2018). With the definition of these two different frames, the surface location on the Moon is differ about 860 m (Davies & Colvin 2000). The applicable areas of these two different system is also slightly different. The PA frame is useful for dynamical studies of the Moon, i.e., gravity field determination and lunar laser ranging (LLR) (LRO Project 2008). Meanwhile, the ME frame is recommended as for cartographic products as past products have been aligned to the ME frame (Archinal et al. 2011) to be consistent with heritage of Planetary Data System (PDS) datasets (LRO Project 2008).

For the KPLO mission, spacecraft’s states in the PA frame for any epoch is transferred by using the JPL Developmental Ephemeris (DE) ephemeris, especially, DE430 (Archinal et al. 2018). The direction cosine matrix which transforms ICRF to the PA frame, $D I C R F P A$ , can be obtained as (Archinal et al. 2011):

D I C R F P A = R 3 (ψ) R 1 (θ) R 3 (φ)

(8)

where, φ is the angle along the ICRF equator, measured from the ICRF X-axis to the ascending node of the lunar equator, θ is the lunar equator inclination vector to the ICRF equator, and ψ is the angle measured along the lunar equator from the node to the lunar prime meridian. These three Euler angles (φ, θ, ψ) represent physical librations of the Moon and can be obtained from JPL DE ephemeris series. In Eq. (8), the standard rotation matrices, R₁ and R₃, for righthanded rotations with arbitrary angle η are defined as in Eq. (9). The subscripts 1 and 3 in R₁ and R₃, refers X and Z axes, respectively.

R 1 (η) = (100 0 c η s η 0 − s η c η)

(9a)

R 3 (η) = (c η s η 0 − s η c η 0 001)

(9b)

With direction cosine matrix, $D I C R F P A$ , shown in Eq. (8), s_ICRF can simply be transformed to the Moon PA frame as follows:

s P A = T I C R F P A s I C R F

(10)

where $T I C R F P A$ is

T I C R F P A = (D I C R F P A 0 D ˙ I C R F P A D I C R F P A)

(11)

and, $D I C R F P A$ and $D ˙ I C R F P A$ can be obtained as following.

D I C R F P A = (c ψ c ϕ − s ψ s ϕ c θ c ψ s ϕ +s ψ c θ c ϕ s ψ s θ − s ψ c ϕ − c ψ s ϕ c θ − s ψ s ϕ +c ψ c θ c ϕ c ψ s θ s θ s ϕ − s θ s ϕ c θ)

(12)

D ˙ I C R F P A (1, 1) = (− ϕ ((c ψ s ϕ) + (s ψ c ϕ c θ)) + θ ˙ (s ψ s ϕ s θ) − ψ ˙ ((s ψ c ϕ) + (c ψ s ϕ c θ))) D ˙ I C R F P A (1, 2) = (ϕ ˙ ((c ψ c ϕ) − (s ψ c θ s ϕ)) − θ ˙ (s ψ s θ c ϕ) − ψ ˙ ((s ψ s ϕ) − (c ψ c θ c ϕ))) D ˙ I C R F P A (1, 3) = (θ ˙ (s ψ c θ) + ψ ˙ (c ψ s θ)) D ˙ I C R F P A (2, 1) = (ϕ ˙ ((s ψ s ϕ) − (c ψ c ϕ c θ)) + θ ˙ (c ψ s ϕ s θ) − ψ ˙ ((c ψ c ϕ) − (s ψ s ϕ c θ))) D ˙ I C R F P A (2, 2) = (− ϕ ˙ ((s ψ c ϕ) + (c ψ c θ s ϕ)) − θ ˙ (c ψ s θ c ϕ) − ψ ˙ ((c ψ s ϕ) + (s ψ c θ c ϕ))) D ˙ I C R F P A (2, 3) = (θ ˙ (c ψ c θ) − ψ ˙ (s ψ s θ)) D ˙ I C R F P A (3, 1) = (ϕ ˙ (s θ c ϕ) + θ ˙ (c θ s ϕ)) D ˙ I C R F P A (3, 2) = (ϕ ˙ (s θ s ϕ) − θ ˙ (c θ c ϕ)) D ˙ I C R F P A (3, 3) = (− θ ˙ s θ)

(13)

In Eq. (13), $φ ˙, θ ˙, and ψ ˙$ are Euler angle rates which also can be obtained from JPL DE series.

2.3 Moon Mean Earth (ME) Frame

As already discussed, IAU WG on CCRE continuously approximated and revised recommendations on the direction of the Moon’s north pole and prime meridian using closed formulae for the ME frame. However, recent report no longer provides those formulae (Davies & Colvin 2000) as they are only accurate to approximately 150 m (Konopliv et al. 2001). Therefore, it is recommended to use a precise lunar ephemeris (i.e., JPL DE series) to obtain states in the PA frame by using numerically integrated the libration angles first, as shown in subsection 2.2, and then use following state transition matrix to obtain the states in the Moon ME frame (Folkner et al. 2014;Archinal et al. 2018).

D P A M E = R 1 (− 0.28 5 ″) R 2 (− 78.58 0 ″) R 3 (− 67.57 3 ″)

(14)

where R₂ is the standard rotation matrix around Y axis which can be defined as with arbitrary angle η as:

R 2 (η) = (c η 0 − s η 010 s η 0 c η)

(15)

With direction cosine matrix, $D P A M E$ , states in the Moon PA frame, s_PA, can be transformed to the Moon ME frame as follows:

s M E = T P A M E s P A

(16)

where $T P A M E$ is defined as:

T P A M E = (D P A M E 0 0 D P A M E)

(17)

In here, reader must note that the those of three Euler angle values given in Eq. (14) is only valid when JPL DE430 ephemeris is used, and may differ for other ephemeris. In addition, states in the Moon ME frame is equivalent to states in the Moon Fixed frame for the KPLO flight dynamics data.

2.4 Moon True of Date (TOD) frame

KPLO flight dynamics data will often be expressed in the Moon TOD frame which is not defined in previous literatures (Roncoli 2005;LRO Project 2008). However, the Moon TOD frame will be very useful to monitor the KPLO’s flight status, such as precise orbital inclination maintenance status during the flight with respect to the current epoch. This is because as the Moon TOD frame is a quasi-inertial frame referenced to Moon’s mean equator based at the current epoch. To convert s_ICRF to s_TOD, following direction cosine matrix, $D I C R F T O D$ , can be applied.

D I C R F T O D = [x ¯ T O D y ¯ T O D z ¯ T O D]

(18)

In Eq. (18), the unit vector of z-axis direction, $z ¯ T O D$ , of the Moon TOD frame can be obtained:

z ¯ T O D = [D I C R F P A] − 1 [D P A M E] − 1 z ¯ M E

(19)

where $z ¯ M E$ is the unit vector of z-axis direction, $z ¯ M E = [0 0 1] T$ , of the Moon ME frame. $z ¯ M E$ is used to obtain $z ¯ T O D$ as the z-axis of the Moon TOD frame is defined as to be aligned with the z-axis of the Moon ME frame. The unit vector of x-axis direction, $x ¯ T O D$ , of the Moon TOD frame can be obtained using $x ¯ T O D = z ¯ I C R F × z ¯ T O D / ‖ z ¯ I C R F × z ¯ T O D ‖$ . Finally, the unit vector of y-axis direction, $y ¯ T O D$ , can be determined using $y ¯ T O D = z ¯ T O D × x ¯ T O D / ‖ z ¯ T O D × x ¯ T O D ‖$ . Note that these unit vectors are evaluated at each given time to formulate the Moon TOD frame. With $D I C R F T O D, s I C R F$ can be transformed to s_TOD as follows:

s T O D = T I C R F T O D s I C R F

(20)

where $T I C R F T O D$ is

T I C R F T O D = (D I C R F T O D 0 0 D I C R F T O D)

(21)

3. Transformation Examples

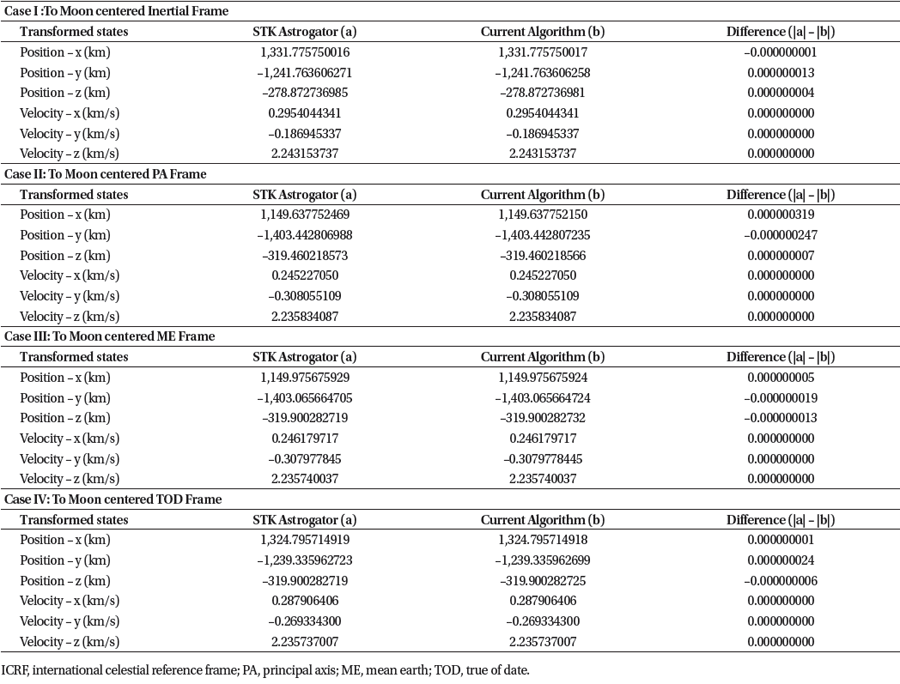
Current subsection provides examples of transformation results utilizing algorithms shown in previous subsection. In Table 1, initial states as well as time condition are provided that are used for transformation test examples.

Table 1. Initial states and time condition used for test examples

Download Excel Table

Using initial state and time conditions shown in Table 1, states are transformed to each four different lunar reference frames: Moon centered - Inertial, PA, ME, and TOD frames, respectively, and example of transformation result is shown in Table 2. The results shown in Table 2 is generated using MATLAB compiler based on the transformation algorithm discussed previously. To validate performance of current transformation algorithms, same frame transformation is also conducted with the same initial conditions using performance proven Commercial Off-the-Shelf (COTS) software, the STK Astrogator, and performance is also compared in Table 2. As shown in Table 2, frame transformation results between STK Astrogator show far less than mm in position and almost none in velocity component, respectively. Current results show that those of lunar frames can be transformed from/to very precisely to each other based on the current transformation algorithm. By providing an example of practical lunar reference frame transformations, results in this subsection can further be usefully used to user community who are establishing their own script to post process the KPLO flight dynamics data.

Table 2. Example transformation results: Transformed from Moon centered ICRF to Moon centered - Inertial, PA, ME, and TOD frames, respectively

Download Excel Table

4. CONCLUSION

In this work, the practical transformation algorithms for the several lunar reference frames is defined and provided for the KPLO flight operations as well as science data post processing. Unlike previous literatures, current work is more focused on the practical aspects of lunar reference frames transformations algorithms. Therefore, detailed step by step implementation procedure is presented to support wide ranges of the KPLO flight dynamics data user community, in particular, users who are unfamiliar with lunar reference frame transformations. Practical transformation algorithms from the ICRF to four different lunar reference frames (Moon Inertial, Moon PA, Moon ME which is equivalent Moon Fixed, and Moon TOD) are presented in as much as detail as possible. Cautionary points while implementing transformation procedures is also specified to minimize trial errors of KPLO flight data user community. Example transformation results are also provided including crosschecked results against to the flight proven STK Astrogator’s results which showed that transformation can be conducted very precisely with the current algorithms. Through this work, common understandings of reference frames that will be used throughout the KPLO mission operation can be established. Moreover, KPLO flight dynamics data can be reprocessed very accurately by using current algorithms to meet the needs of not only the KPLO team members but also KPLO flight data users world-wide for the new science discovery.

Acknowledgments

This work was supported by the Korea Aerospace Research Institute (KARI) (under a contract with the Ministry of Science and ICT) through the “Development of Pathfinder Lunar Orbiter and Key Technologies for the Second Stage Lunar Exploration” project (no. 2016M1A3A9005561).

References

Archinal BA, Acton CH, A’Hearn MF, Conrad A, Consolmagno GJ, et al., Report of the IAU working group on cartographic coordinates and rotational elements: 2015, Celest. Mech. Dyn. Astron. 130, 22 (2018).

Archinal BA, A’Hearn MF, Bowell E, Conrad A, Consolmagno GJ, et al., Report of the IAU working group on cartographic coordinates and rotational elements: 2009, Celest. Mech. Dyn. Astron. 109, 101-135 (2011).

Bae J, Hong SB, Song YJ, Kim YR, Park J, et al., Trajectory correction maneuver analysis of KPLO WSB/BLT trajectory with respect to burn error and maneuver execution epoch, Bullentin of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Fall Conference, Jeju, Korea, 18-20 Nov 2020a.

Bae J, Kim YR, Song YJ, Park J, Hong SB, et al., Maneuver recovery function development and result analysis of trajectory correction maneuver of Korea Pathfinder Lunar Orbiter, Bullentin of the Korea Space Science Society (KSSS) 2020 Fall Conference, Jeju, Korea, 28-30 Oct 2020b.

Bae J, Kim YR, Song YJ, Park J, Hong SB, et al., Maneuver recovery process of lunar orbiter insertion maneuver considering engine model for Korea Pathfinder Lunar Orbiter, Bulletin of the Korea Space Science Society (KSSS) 2021 Spring Conference, Yeosu, Korea, 28-30 Apr 2021.

Bae J, Lee D, Song YJ, Kim YR, Park JI, et al., Trajectory correction maneuver design of KPLO BLT trajectory considering flight operation, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Spring Conference, Goseong, Korea, 8-11 Jul 2020c.

Davies ME, Colvin TR, Lunar coordinates in the regions of the Apollo landers, J. Geophys. Res. 105, 20277-20280 (2000).

Folkner WM, Williams JG, Boggs DH, Park RS, Kuchynka P, The planetary and lunar ephemerides DE430 and DE431, California Institute of Technology, IPN Progress Report 42- 196 (2014).

Hong S, Kim YR, Song YJ, Lee D, Park JI, et al., Launch vehicle dispersion analysis of KPLO BLT trajectory, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Spring Conference, Goseong, Korea, 8-11 Jul 2020a.

10.

Hong SB, Park J, Kim IK, Song YJ, Kim YR, et al., KPLO ground station tracking time analysis, Bullentin of the Korea Space Science Society (KSSS) 2020 Fall Conference, Jeju, Korea, 28- 30 Oct 2020b.

11.

Kim YR, Hong SB, Song YJ, Park J, Bae J, et al., Orbit determination error analysis for design of launch vehicle dispersion trajectory correction maneuver, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Fall Conference, Jeju, Korea, 18-20 Nov 2020a.

12.

Kim YR, Song YJ, Observational arc-length effect on orbit determination for Korea Pathfinder Lunar Orbiter in the Earth-Moon transfer phase using a sequential estimation, J. Astron. Space Sci. 36, 293-306 (2019a).

13.

Kim YR, Song YJ, Bae J, Choi SW, Orbit determination simulation for Korea Pathfinder Lunar Orbiter using sequential estimation approach, Proceedings of the 29^th AAS/AIAA Space Flight Mechanics Meeting, Maui, HI, 13-17 Jan 2019b.

14.

Kim YR, Song YJ, Bae J, Park J, Hong SB, et al., Ground tracking support condition effect on orbit determination and prediction for Korea Pathfinder Lunar Orbiter for trans-lunar trajectory, Bulletin of the Korea Space Science Society (KSSS) 2021 Spring Conference, Yeosu, Korea, 28-30 Apr 2021.

15.

Kim YR, Song YJ, Park JI, Lee D, Bae J, et al., Orbit determination simulation for Korea Pathfinder Lunar Orbiter using ballistic lunar transfer, Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA, 9-13 Aug 2020b.

16.

Kim YR, Song YJ, Park J, Lee D, Bae J, et al., Ground tracking support condition effect on orbit determination for Korea Pathfinder Lunar Orbiter (KPLO) in lunar orbit, J. Astron. Space Sci. 37, 237-247 (2020c).

17.

Konopliv AS, Asmar SW, Carranza E, Sjogren WL, Yuan DN, Recent gravity models as a result of the lunar prospector mission. Icarus. 150, 1-18 (2001).

18.

Lee D, Park J, Song Y, Kim Y, Hong S, et al., KPLO BLT trajectory design, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Spring Conference, Goseong, Korea, 8-11 Jul 2020a.

19.

Lee D, Park J, Song YJ, Kim YR, Hong SB, et al., WSB/BLT trajectories for the KPLO mission, Bulletin of the Korea Space Science Society (KSSS) 2020 Fall Conference, Jeju, Korea, 28-30 Oct 2020b.

20.

Lee D, Park J, Song YJ, Kim YR, Hong SB, et al., Lunar orbit conditions to design WSB/BLT trajectories, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Fall Conference, Jeju, Korea, 18-20 Nov 2020c.

21.

LRO Project, A standardized lunar coordinate system for the lunar reconnaissance orbiter and lunar datasets, LRO Project and LGCWG White Paper, ver. 5, Goddard Space Flight Center, MD (2008).

22.

Navigation Ancillary Information Facility [NAIF], SPICE Data (SPICE Kernels) (2021) [Internet], viewed 2021 Mar 17, available from: https://naif.jpl.nasa.gov/naif/data.html

23.

Park J, Lee D, Hong SB, Song YJ, Kim YR, et al., KPLO lunar mission orbit design using eccentricity-argument of periapsis vector, Bulletin of the Korea Space Science Society (KSSS) 2020 Fall Conference, Jeju, Korea, 28-30 Oct 2020a.

24.

Park JI, Lee D, Kim YR, Song YJ, Hong S, et al., Lunar orbit insertion and mission orbit design for KPLO BLT trajectory, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Spring Conference, Goseong, Korea, 8-11 Jul 2020b.

25.

Roncoli RB, Lunar constants and models document, Jet Propulsion Laboratory, California, JPL Technical Document D-32296 (2005).

26.

Song YJ, Kim YR, Bae J, Kim BY, Evolution of the selenopotential model and its effects on the propagation accuracy of orbits around the Moon, Math. Prob. Eng. 2017, 5493679 (2017).

27.

Song YJ, Kim YR, Lee D, Park JI, Hong S, et al., Impact of OP errors to the KPLO lunar orbit insertion utilizing BLT, Proceedings of the Korea Society for Aeronautical and Space Science (KSAS) 2020 Spring Conference, Goseong, Korea, 8-11 Jul 2020a.

28.

Song YJ, Lee D, Bae J, Kim YR, Park, J, et al., Mission coordinate system definition, precise transformation algorithm and its implementation results for Korea Pathfinder Lunar Orbiter flight dynamics, Bulletin of the Korea Space Science Society (KSSS) 2020 Fall Conference, Jeju, Korea, 28-30 Oct 2020b.