Recent progress in the theoretical understanding of relativistic electron scattering and precipitation by electromagnetic ion cyclotron waves in the Earth’s inner magnetosphere

1. INTRODUCTION

It has long been known that electromagnetic ion cyclotron (EMIC) waves are excited by an anisotropic distribution of energetic ions such that T_⊥>T_∥ at energies of a few 10s keV where T_⊥ and T_∥ refer to the ion perpendicular and parallel temperatures relative to the background magnetic field, respectively (Cornwall 1965; Kennel & Petschek 1966). Such anisotropy can be driven by substorm injections and solar wind dynamic pressure enhancements, as confirmed by recent observational tests (e.g., Cho et al. 2016, 2017;Noh et al. 2018;Remya et al. 2018).

It is widely believed that EMIC waves cause atmospheric precipitation of relativistic electrons and energetic ions in the inner magnetosphere by pitch angle scattering. Since the earliest theoretical suggestion by Kennel & Petschek (1966), a number of observational reports supporting particle precipitation due to EMIC waves have accumulated to a large extent (Imhof et al. 1977,1986;Bortnik et al. 2006;Sandanger et al. 2007, 2009; Yahnin & Yahnina 2007; Miyoshi et al. 2008;Rodger et al. 2008;Yuan et al. 2013;Li et al. 2014;Blum et al. 2015;Zhang et al. 2016;Hendry et al. 2016, 2017;Kurita et al. 2018;Qin et al. 2018;Woodger et al. 2018).

The original work by Kennel & Petschek (1966) was followed by further theoretical studies by Cornwall et al. (1970) on proton loss in the ring current region and by Thorne & Kennel (1971) on loss of relativistic electrons. Lyons & Thorne (1972) advanced the idea by specifically formulating the bounce-averaged diffusion coefficients based on quasilinear diffusion theory (Kennel & Engelmann, 1966). Efforts in theory and simulations have continued with more extensive and realistic estimations of the diffusion coefficients in both the quasilinear and nonlinear regimes, the results of which have indicated a positive relationship between EMIC waves and particle precipitation (Jordanova et al. 1997, 2001, 2008;Lorentzen et al. 2000;Albert 2003;Summers & Thorne 2003;Li et al. 2007;Albert & Bortnik 2009;Lemons et al. 2009;Shprits et al. 2009;Liu et al. 2010, 2012;Ukhorskiy et al. 2010;Xiao et al. 2011;Shoji & Omura 2012;Su et al. 2012;Zhu et al. 2012;Omura & Zhao 2012, 2013; Shprits et al. 2013, 2016;Kersten et al. 2014;Kubota et al. 2015;Kang et al. 2015, 2016;Chen et al. 2016;Wang et al. 2017;Ni et al. 2015, 2018;Lee et al. 2018).

The present paper is intended to review the major advances in research on relativistic electron precipitation by EMIC waves that have been made over the last 15 years or so. This review is exclusively devoted only to the theoretical and simulation works. The author stresses that this review is not intended to be exhaustive, so it may unintentionally miss some of the published papers. Nevertheless, the review is written with hope that it addresses the major progress in this field over the last 15 years or so. The review focuses on the following topics: (i) quasilinear resonant diffusion simulations, which constitute the majority of the efforts in this field, (ii) nonlinear and nonresonant interactions, which are not reflected in quasilinear resonance theory and have received increasing attention from the community in recent years, (iii) effects of oblique wave propagation and noncircular wave polarization on the pitch angle scattering, which need to be incorporated for realistic modeling, (iv) possible ways to scatter near-equatorial pitch angle electrons such as by a Landau resonance, a bounce resonance, or an electron interaction with EMIC and other waves together, and finally (v) the interaction of relativistic electrons with EMIC waves with a time varying frequency such as a rising tone emission, which has often been reported from observations. The paper concludes with suggestions of a few promising topics for further progress in this field.

2. PROGRESS FROM QUASILINEAR RESONANCE THEORY

The standard quasilinear resonant diffusion formalism, which has been widely used in the research community to model radiation belt dynamics, was originally developed by Kennel & Engelmann (1966) and extended by Lyons et al. (1972) and Lyons (1974a, b). This formalism is valid under the assumption of a weak amplitude wave and in the limit of resonant diffusion where the wave growth rate becomes zero. The limit of the small growth rate of waves compared to the particle gyro-period implies that the particle distribution is independent of the particle’s Larmor phase. Thus, diffusion in this formalism is considered to take place on a timescale much longer than the particle gyro-period. The resonant diffusion is evaluated based on the cyclotron resonance condition defined by $\omega -k_{\parallel }{V}_{\parallel }=\frac{N\left|{\Omega }_e\right|}{\gamma }$, where N=0,±1,±2,⋯ is the resonance harmonic number, $\gamma ={\left[1-{\left(\frac{V}{c}\right)}^2\right]}^{-\frac{1}{2}}$ is the relativistic factor, υ is the electron velocity, c is the speed of light, |Ω_e| is the local electron gyrofrequency, and k_∥ and v_∥ are the components of the wave propagation vector and particle velocity parallel to the ambient magnetic field, respectively (Kennel & Petschek 1966).

The quasilinear resonant diffusion in the pitch angle α of the particle distribution function f of a given species is governed by the following equation.

where $D_{\alpha \alpha }^{QL}$ is the local diffusion coefficient, $〈D_{{\alpha }_{eq}{\alpha }_{eq}}^{QL}〉$ is the bounce-averaged diffusion coefficient, $G=T\left({\alpha }_{eq}\right)\text{sin}\hspace{0.33em}{\alpha }_{eq}\hspace{0.33em}\text{cos}\hspace{0.33em}{\alpha }_{eq},\hspace{0.33em}T\left({\alpha }_{eq}\right)\approx 1.3-0.56\hspace{0.33em}\text{sin}\hspace{0.33em}{\alpha }_{eq},\hspace{0.33em}\text{and}\hspace{0.33em}{\alpha }_{eq}$ is the equatorial pitch angle.

The local diffusion coefficients can be written as a sum over all harmonics and an integral over k_⊥ to reflect a wave normal angle distribution, and specific wave information and an appropriate dispersion relation enter into this formalism.

Summers & Thorne (2003) applied quasilinear diffusion theory to the resonant interaction between relativistic electrons and EMIC waves in a multi-ion (H⁺, He⁺, O⁺) plasma under typical inner magnetospheric conditions. Although they used a simple functional form for the local diffusion coefficient $D_{\alpha \alpha }^{QL}$, the calculation results clearly demonstrated the dependence of the pitch angle diffusion by EMIC waves on the equatorial pitch angle and kinetic energy: the diffusion is significant for a pitch angle range from zero to some upper bound, which shifts toward (but is always below) 90° as the kinetic energy increases. In addition, they estimated the minimum kinetic energy required for electrons to resonate with EMIC waves, which depends on the value of the ratio of the electron plasma frequency to the electron gyrofrequency, the properties of the EMIC wave spectrum and the ion compositions. Similar results for the local diffusion coefficients were obtained by the work of Albert (2003), which was based on slight approximations and computational techniques that allow efficient calculation of the diffusion coefficients. The work by Albert (2003) included bounce-averaged diffusion coefficients that differed qualitatively from the local values.

Soon after Summers & Thorne (2003) and Albert (2003), a complete scheme for calculations of the quasilinear diffusion coefficients was developed by Glauert & Horne (2005), which can be applied to various plasma waves such as EMIC, whistler mode chorus, hiss, and Z mode waves. The scheme emphasizes the bounce average of the diffusion coefficients. Many simulations are based on a similar formulation. For example, Li et al. (2007) adopted a rather simplified model of EMIC waves in a quasilinear (both bounce- and Magnetic Local Time (MLT)-averaged) diffusion simulation such that EMIC waves were present at latitudes below 15° with a specific set of wave spectral properties and the electrons were exposed to such EMIC waves for 5 % of their drift time during the storm main phase. The results indicated that EMIC waves scatter electrons preferably with small pitch angle electrons although the pitch angle range for scattering becomes broader for a larger kinetic energy, consistent with the earlier theoretical predictions by Summers & Thorne (2003) and Albert (2003).

The later work by Jordanova et al. (2008) is distinguished from those of Summers & Thorne (2003), Albert (2003), and Li et al. (2007) in the following sense. Jordanova et al. (2008) obtained EMIC waves that were generated self-consistently from anisotropic ring current ion populations in a kinetic Ring current-Atmosphere interactions Model (RAM) (Jordanova & Miyoshi 2005) and then used the EMIC waves to compute the relativistic electron pitch angle diffusion coefficients of Albert (2003). Therefore, their simulation reflects coupling between the ring current ions having low energy and the relativistic energy electrons via the EMIC waves. This approach was applied to a specific storm time, although no comparison between the simulations and observations was actually made. The simulation results indicated that precipitation by EMIC waves results in a large loss of radiation belt electrons at energy ≥ 1 MeV for L < 5 for the studied storm event.

A subsequent quasilinear diffusion simulation by Shprits et al. (2009) addressed an important aspect regarding the significance of pitch angle scattering by EMIC waves in which they used the same simple wave model as in Li et al. (2007). Unlike previous simulations that computed a drift and bounce-averaged rates of scattering based on the assumption that the overall timescale for relativistic electron loss is much longer than the electron drift time, the simulation by Shprits et al. (2009) considered MLT-dependent diffusion, taking into account the diffusion that may be locally comparable to or exceeding the strong diffusion limit (Kennel 1969). Such strong diffusion is characterized by a diffusion rate faster than the losses to the atmosphere and ultimately by an isotropic pitch angle distribution throughout the loss cone (Kennel 1969). During such a process, many particles that enter into the loss cone are scattered back out of the loss cone before completing a quarter bounce, which limits the net loss. The simulation results indicated that the MLT-averaged simulations may not accurately treat such a locally strong diffusion process and tend to overestimate net loss during a storm.

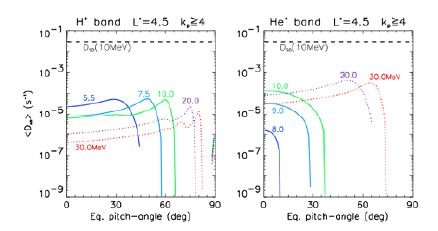
A more realistic simulation was performed years later. Kersten et al. (2014) tried to be realistic in quasilinear diffusion simulations by using the EMIC wave properties measured by the Combined Release and Radiation Effects Satellite (CRRES) needed for calculating the diffusion rates. The wave database contains the peak spectral intensity, the frequency of the peak spectral intensity, the spectral width in frequency, and the wave intensity integrated over the waveband. They assumed that the EMIC waves are present over all latitudes but over the 6 h MLT zone in the afternoon sector. The simulations indicated that EMIC waves cause a large dropout in the electron flux for energies > 2 MeV but only for pitch angles smaller than a certain upper bound value. This is easily confirmed from Fig. 1, indicating that the diffusion coefficients are significant only up to ~60° for < 10 MeV (H⁺ band) and < 20 MeV (He⁺ band). Consequently, they claimed that it is not likely that EMIC waves impose an upper limit on the energy of the flux of radiation belt electrons. A similar conclusion was reached from a quasilinear diffusion calculation performed by Usanova et al. (2014), where the loss of ultrarelativistic electrons due to EMIC wave scattering is limited to pitch angles < ~45°.

Fig. 1. Bounce-averaged pitch angle diffusion coefficients for (left) H⁺ band and (right) He⁺ band EMIC waves for selected energies calculated using the Pitch Angle and Energy Diffusion of Ions and Electrons (PADIE) code (Glauert & Horne 2005). The strong diffusion rate (D_SD) for E = 10 MeV is also shown. Taken from Kersten et al. (2014).

Download Original Figure

A subsequent work by Ni et al. (2015) made further progress by adopting latitudinally varying models for the wave normal angle of waves of three bands (H⁺-, He⁺-, and O⁺-band waves) in quasilinear diffusion simulations. This approach led them to find a few interesting features. First, the obliquity of EMIC waves decreases the efficiency of relativistic electron pitch angle scattering. They also found that EMIC waves of 1 nT produce intense scattering losses for an outer radiation belt relativistic electron on time scales of < 1 min to ~1 h. In addition, H⁺-band and He⁺-band waves are most efficient in pitch angle scattering loss of 1-2 MeV electrons, whereas O⁺-band waves can dominate the loss of 5-10 MeV electrons. Thus, different EMIC bands play a role at different energies. Last, scattering by EMIC waves cannot affect large pitch angles, leading to top-hat-type pitch angle profiles. This led the authors to conclude that the EMIC-wave-driven scattering effect alone is not sufficient to explain the main dropout events of relativistic electrons in the outer radiation belt.

Kang et al. (2016) seemed to have reached a more optimistic conclusion from their simulation using the Radiation Belt Environment (RBE) model (Fok et al. 2011). In that simulation, they incorporated EMIC waves within 12 - 18 MLT (with a time average) obtained from the CRRES observations (Kersten et al., 2014), binned by the Kp index, and applied this EMIC wave to a specific storm time event of a flux dropout identified from the Solar Anomalous and Magnetospheric Particle Explorer (SAMPEX). The simulation reproduced well the electron flux evolution of >2.5 MeV around the times of the flux dropout. However, this comparison was based on electrons with equatorial pitch angles < 10° because of the highly inclined low-Earth orbit of SAMPEX.

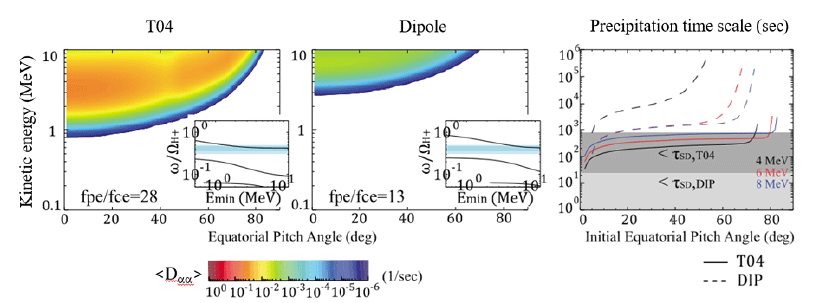
The effect of a background magnetic field on the diffusion coefficient was also considered. A quasilinear diffusion simulation by Kang et al. (2015) used the Tsyganenko 04 (T04) magnetic field model to compute diffusion coefficients and compare them with those obtained based on a dipole magnetic field model. The results indicated that the diffusion rates of relativistic electrons due to EMIC waves were enhanced and precipitation time scales were reduced compared to those obtained from a dipole model. This feature is summarized in Fig. 2. They suggested that the main cause for this result is the reduction in the magnetic field in the T04 model.

Fig. 2. (Left and middle) Comparison of the two-dimensional bounce-averaged pitch angle diffusion rates <D_αα> of the T04 model and the dipole model. (Right) Comparison of the precipitation time scales between the T04 model (solid) and the dipole (dashed) models for selected energies. Taken from Kang et al. (2015).

Download Original Figure

As it became clear that the efficiency of quasilinear resonant diffusion depends on not only the pitch angle but also the kinetic energy of the electrons, the simulation by Shprits et al. (2016) focused on emphasizing the different efficiencies of pitch angle scattering precipitation by EMIC waves between relativistic (~1 MeV or less) and ultrarelativistic (≳ a few MeV) electrons. By considering a spectral model of EMIC waves that exist at 5 % of the electron orbit and after applying the model to a specific storm time in the radiation belt measured by the Van Allen Probes, their simulation with the inclusion of the EMIC wave model reproduced the ultrarelativistic electron flux dropout identified from the Van Allen Probes observations, while it did not affect the relativistic electron evolution. An important suggestion from this result is that EMIC waves cause effective loss of the highest energy electrons and can determine an uppermost energy for the trapped electrons, unlike the earlier suggestions by Kersten et al. (2014) and Usanova et al. (2014).

A more recent effort included the reflection of the EMIC waves by considering their dependence on solar wind and geomagnetic conditions into the quasilinear diffusion simulations. Drozdov et al. (2017) considered how the occurrence of an EMIC wave depends on the Dst, Kp, and AE indices, the solar wind speed, and the solar wind dynamic pressure. In their simulations performed with the Versatile Electron Radiation Belt (VERB) quasilinear diffusion code, EMIC waves were included in the simulation only if any of the above five parameters was larger (or smaller in the case of Dst) than a threshold value. By comparing their many simulations with the observations of the Van Allen Probes, they arrived at the conclusion that the diffusion simulation with EMIC waves, when parameterized by the solar wind dynamic pressure, provides best agreement with the observations among considered parameterizations. Although this was not based on the reflection of precise EMIC wave information, the conclusion emphasizes the significant role of the dynamic pressure in EMIC wave-driven electron diffusion.

The intensity of the electron population in the outer radiation belt decreases rapidly beyond ~1-2 MeV. Thus, the significance of resonant scattering of outer radiation belt electrons by EMIC waves is considered to be meaningful when the minimum resonance energy lies at or below this critical energy. From the CRRES observations, Meredith et al. (2003) reported that for most EMIC waves, the minimum resonance energy for electrons is above 2 MeV. In contrast, Ukhorskiy et al. (2010) noted that the EMIC wave power is often nonnegligible for a rather broad frequency range and that the resonant interaction of such waves with electrons does not have to be restricted to a single frequency where the EMIC wave power peaks. Based on this idea, they suggested that EMIC waves just below the He⁺ gyrofrequency can interact with electrons below 2 MeV. In addition, it has been suggested that the minimum energy of the electron cyclotron resonance is theoretically a sensitive function of warm plasma factors. By solving the kinetic dispersion relation for EMIC waves in a multicomponent plasma for various parameter conditions, several authors (Chen et al. 2011;Silin et al. 2011, Gary et al. 2012, Lee et al. 2017) concluded that the EMIC wave growth depends on a relative fraction of warm heavy ions and their temperature and anisotropy. In particular, Chen et al. (2011) suggested that the maximum wavenumber for which the electron resonance energy is near 1 MeV can be obtained for the conditions of a large cold plasma density such as inside the plasmasphere and a large proton anisotropy such as during the storm time. Based on the same kinetic dispersion relation, Gary et al. (2012) found that if the He⁺ ion temperature is much lower than that of the protons and the He⁺ ion density is large enough, the He⁺ branch EMIC wave with a large wavenumber can become unstable. Such a wave can resonate with electrons of 500 keV - 2 MeV. Lee et al. (2017) advanced the work by Gary et al. (2012) by allowing warm He⁺ anisotropy into the kinetic dispersion relation. This led to the suggestion that, for the cold plasma dominant condition such as inside the plasmasphere, the effect of the anisotropic He⁺ temperature leads to the existence of an unstable He⁺-band wave at a large wavenumber even when the He⁺ temperature is very high. In other words, in this case, the He⁺ temperature does not need to be too low for an unstable He⁺-band wave to exist at a large wavenumber as long as sufficient anisotropy of the He⁺ temperature is provided.

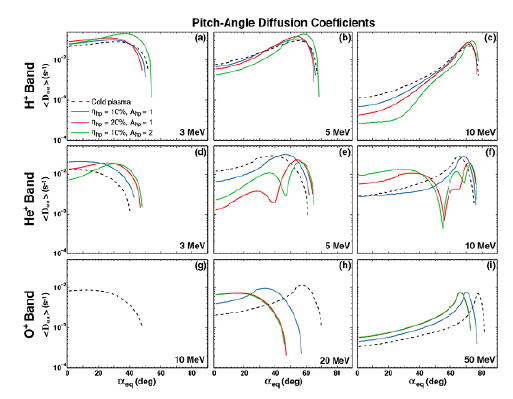
Motivated by the warm plasma effect found in previous works (Chen et al. 2011;Silin et al. 2011, Gary et al. 2012, Lee et al. 2017), Ni et al. (2018) calculated the bounce-averaged quasilinear diffusion coefficients by using the kinetic dispersion relation. Although they included only hot protons in the kinetic dispersion relation, this inclusion still makes a significant difference, particularly for the resonance frequency and wave group velocity, which then leads to resonance energy and pitch angle diffusion coefficients that are notably different from those obtained using the cold plasma dispersion relation. This is shown in Fig. 3, where the diffusion coefficients are compared between the cold plasma dispersion relation (dashed) and kinetic dispersion relation with three different conditions (solid) for EMIC waves in three frequency bands and three selected energies.

Fig. 3. Bounce-averaged pitch angle diffusion coefficients <D_αα> at L = 4.5 for selected electron energies and the EMIC waves in three frequency bands. The dashed black curve refers to the diffusion coefficients obtained using the cold plasma dispersion relation, and the solid curves represents the diffusion coefficients obtained using the hot plasma kinetic dispersion relation. Taken from Ni et al. (2018).

Download Original Figure

3. NONLINEAR AND NONRESONANT EFFECTS

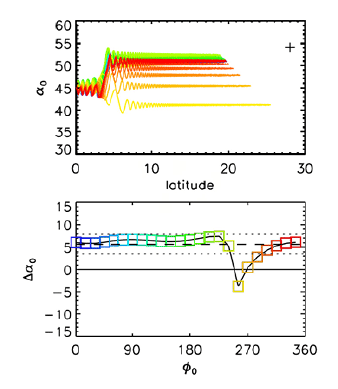
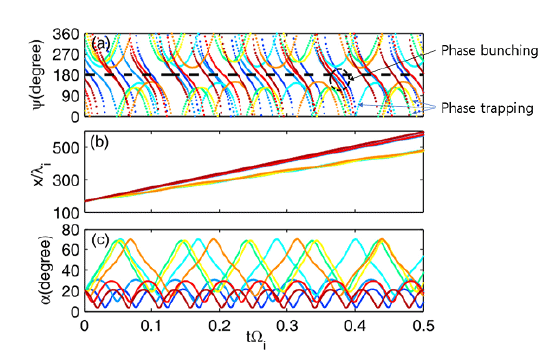
The quasilinear resonant diffusion formalism misses some nonlinear physics elements, which may be important in determining the pitch angle scattering. Albert & Bortnik (2009) suggested that a nonlinear interaction of relativistic electrons can occur even with moderate-amplitude EMIC waves, which can lead to advection toward high pitch angles rather than diffusion toward the loss cone. This effect can decrease the overall precipitation loss rate of electrons. This was the first report emphasizing the potential importance of the nonlinear aspect of the interaction between EMIC waves and relativistic electrons, which is not addressed in quasilinear theory. Fig. 4 demonstrates an example where the pitch angle changes of electrons with various initial phases are significantly nonlinear in phase and exhibit a phase bunching effect after encountering EMIC waves, resulting in an advective change in pitch angle.

Fig. 4. (upper panel) Pitch angle along the field lines of 24 electrons with different initial phases, an energy of E= 2 MeV and α₀ = 45° under EMIC wave influence. (lower panel) Nonlinear aspect of pitch angle change in initial phase. Taken from Albert & Bortnik (2009).

Download Original Figure

Nonlinear effects were further examined by Liu et al. (2010, 2012) in a more comprehensive study, though in a uniform plasma. Liu et al. (2010) carried out test particle computations of scattering for electrons with 2 MeV due to EMIC waves which were created in a self-consistent way from a hybrid simulation. By carrying out quasilinear calculations as well, they focused on the difference in the effect of diffusion between the quasilinear and test particle nonlinear calculations. They found that although both calculations agreed well for small-amplitude EMIC waves, quasilinear theory overestimated the pitch angle diffusion coefficient for EMIC waves with a large amplitude, particularly at high L values.

Liu et al. (2012) focused on demonstrating the physics of nonlinear phase bunching and trapping of electrons in EMIC waves (see Fig. 5). They suggested that the phase bunching and trapping of electrons lead to nonlinear advection. An interesting result is that such an advection develops toward a resonant pitch angle at which the electrons having a specific energy can resonate with the wave. This is in addition to the advection which is inherently present in the quasilinear diffusion equation. They reported that this effect remains valid for both monochromatic and broadband waves if the wave amplitude is sufficiently large. For strong broadband EMIC waves, the nonlinear phase bunching and trapping cause the advection and diffusion coefficients to differ from the predictions from quasilinear theory, leading to a weaker precipitation effect. The authors cautioned the readers that as their computations were carried out for a uniform plasma, it is necessary to obtain the diffusion rates averaged over a bounce period for an application to the radiation belts. Bounce average may affect the significance of the phase bunching and trapping effects.

Fig. 5. (a) The evolution of the relative phase between the perpendicular wavevector and the perpendicular electron velocity vector ψ, (b) the travel distance along the background magnetic field x, and (c) the pitch angle α of 8 tested electrons (different colors) with different phases. A monochromatic EMIC wave of $\frac{\alpha B_{\perp }}{B_0}=0.06$ was taken and initially α = 20°. Taken from Liu et al. (2012).

Download Original Figure

Other studies employed a dipole field to examine the nonlinear interaction of relativistic electrons with an EMIC wave (Su et al. 2012, 2013). Importantly, Su et al. (2012) computed bounce-averaged advection and diffusion coefficients using test particle calculations and compared them with those from quasilinear diffusion simulations. This bounce averaging calculation in a dipole field constituted progress from the earlier work by Liu et al. (2012), which was performed based on the definitions of advection and diffusion coefficients as shown below.

where ∆t^TP is the electron travel time between the equator and mirror point; ${\alpha }_{eq}^{TP}$ is the final equatorial pitch angle; the overline $\overline{\dots }$ represents an averaging over the initial phase; and 〈⋯〉 refers to bounce averaging.

For a reference, it is instructive to demonstrate that the quasilinear bounce-averaged kinetic equations of relativistic electrons can be expressed in a form with an advective diffusion term as shown below.

where the bounce-averaged advection coefficient is defined by

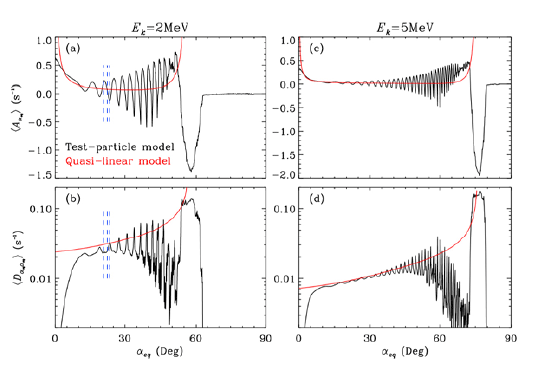
In Su et al. (2012), the advection coefficients of the test particle model, Eq. (2), differed sensitively for different equatorial pitch angles and could be both positive and negative, whereas those of the quasilinear model, Eq. (5), are greater than zero in the resonant region. Additionally, unlike the profiles of quasilinear diffusion coefficients, $D_{{\alpha }_{eq}{\alpha }_{eq}}^{QL}$, the profiles of the test particle model, Eq. (3), change sensitively to the equatorial pitch angle. This is demonstrated for two selected energies in Fig. 6. In addition, the authors identified a few different nonlinear processes which act in different ways. It is likely that different nonlinear effects may add up together or compete against one another, making it nontrivial to predict the net flux change.

Fig. 6. (Top) advection and (bottom) diffusion coefficients (bounce-averaged) at two energies due to scattering by EMIC wave. Black and red curves refer to the results from the test particle and quasilinear calculations, respectively. Taken from Su et al. (2012).

Download Original Figure

Su et al. (2013) advanced the work by Su et al. (2012) by investigating the latitudinal dependence of nonlinear interactions of relativistic electrons with EMIC waves in a dipole field. They found a sensitive dependence of the phase trapping and phase bunching effects on the initial latitude, accordingly affecting the transport coefficients. For example, nonlinear phase trapping yields negative advection, indicating that it may enhance the loss efficiency of quasilinear theory (as in the earlier result by Su et al. (2012)), but its effect varies over the electron’s initial latitude. Clearly, all these complicated nonlinear processes together should be considered for reliable modeling of the radiation belts, as suggested by Su et al. (2012, 2013).

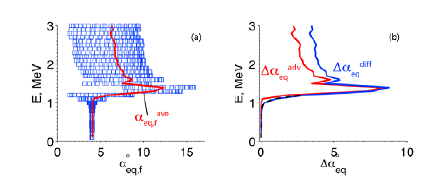
In addition to the traditional resonant interaction, a nonresonant interaction with EMIC waves is also of interest. Such a problem was considered by Chen et al. (2016) for EMIC waves in a dipole field. From the test particle computations, Chen et al. (2016) found that EMIC waves can scatter, in a nonresonant way, the 100s keV electrons (the energy < the minimum resonance energy, ~1.3 MeV in their case). This result is not expected from quasilinear resonant diffusion theory. The authors emphasized that the nonlinear advection effect decreases dramatically below the minimum resonance energy, where the diffusion effect dominates, leading to pitch angle scattering of nonresonant electrons toward the loss cone. Fig. 7(a) demonstrates that for 24 electrons with different initial phases, the final equatorial pitch angle after passing through the EMIC wave zone exhibits a significant advection for a wide energy regime, which drops dramatically below ~1.3 MeV. Fig. 7(b) shows the calculated pitch angle changes due to advection and diffusion, indicating that diffusion is always larger than advection even at an energy below 1.3 MeV.

Fig. 7. (a) Calculated final equatorial pitch angle α_eq,f for 24 electrons with different initial phases for various energies. The relevant parameters taken for this calculation are α_eq,0 = 4°, ${\text{B}}_{wave}^{\text{max}}$ = 1 nT, and $\omega {\Omega }_{\text{O+,eq}}$ = 3.9, and the red line refers to the average ${\alpha }_{eq,f}^{ave}$. (b) Calculated advection transport $\Delta {\alpha }_{eq}^{adv}$ (solid red line) and the diffusion transport $\Delta {\alpha }_{eq}^{diff}$ (blue solid line) for various electron energies E with α_eq,0 = 4°, ${\text{B}}_{wave}^{\text{max}}$ = 1 nT, and $\omega {\Omega }_{\text{O+,eq}}$ = 3.9. Taken from Chen et al. (2016).

Download Original Figure

4. NONLINEAR EFFECTS OF OBLIQUE PROPAGATION AND QUASILINEAR POLARIZATION

It has long been recognized that the wave normal angle of EMIC waves is often not parallel but oblique relative to the background magnetic field due to propagation in an inhomogeneous background plasma and possibly due to wave generation at the oblique wave normal angle. In addition, the wave polarization in many cases deviates from a pure left-hand circular polarization and appears as a noncircular (even quasilinear) or right-hand polarization. These features have been confirmed from various satellite observations (e.g., Anderson et al.,1992;Min et al., 2012;Allen et al., 2015;Saikin et al., 2015;Wang et al., 2017a). Clearly, it is necessary to understand the effects of the oblique wave normal angle and quasilinear polarization on relativistic electron scattering. Currently, there are only a limited number of works on such effects, particularly in the nonlinear regime. While oblique EMIC wave effects have been considered in quasilinear diffusion simulations, for example, in the work by Ni et al. (2015), more physics, particularly the nonlinear aspects, can be obtained from test particle calculations and a comparison with quasilinear calculations.

Wang et al. (2017b) considered oblique EMIC waves in a dipole field and performed test particle calculations (along with quasilinear diffusion calculations for a comparison) to examine the interaction of ultrarelativistic (5 MeV) electrons with the EMIC waves. In particular, they paid attention to the nonlinear fundamental and harmonic resonant scattering of the electrons by considering a relatively large wavenumber so that both the fundamental and harmonic resonances could occur. They found that increasing the wave normal angle causes a stronger nonlinearity in the harmonic resonance but a weaker nonlinearity in the fundamental resonance. A more interesting finding was that compared to the prediction from quasilinear theory, the nonlinear resonances can lead to an ultrarelativistic electron scattering effect for a wider range of pitch angles, which increases as the wave normal angle increases, and it occurs on a faster time scale.

A more systematic study of the effect of a finite wave normal angle and noncircular polarization of monochromatic L-mode EMIC waves on electron scattering was performed by Lee et al. (2018). By employing test particle calculations for a uniform background magnetic field, they computed the advective and diffusive pitch angle changes in wide domains of the energy, pitch angle, wave normal angle, and ellipticity. For this computation, they employed the full expression of the wave-particle phase evolution (shown below (Bell, 1984)), unlike some previous works that missed some of the terms in the equation of the phase difference evolution:

Φ is the wave phase, which is governed by

γ in Eq. (6) is the usual relativistic factor, and ω_1,2 and α_1,2 in Eq. (6) are defined as below.

ε=B_wy/B_wx and ψ is the wave normal angle relative to the background magnetic field B₀.

It is instructive to discuss the terms related to obliquity and noncircular polarization in Eq. (6). The third term on the right-hand side in Eq. (6), k_xυ_x, represents the Doppler effect on the wave frequency, which is due to electron motion perpendicular to the magnetic field across the wave front with an oblique wave normal angle. The second term in the curly brackets in Eq. (6) includes the effect of the noncircular polarization via ω₂ and α₂ defined in Eqs. (8) and (9). The last term in Eq. (6) represents the effect of a background dipole field, which is omitted for the uniform background case. The curly bracket and B_wz terms in Eq. (6) are the wave effect on the phase evolution and may be nonnegligible under certain situations (Inan et al. 1978;Su et al. 2012;Chen et al. 2016).

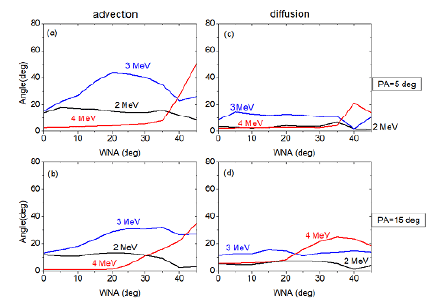
Lee et al. (2018) reported a few interesting results. These results are summarized below, and Fig. 8 shows some of the results from Lee et al. (2018). First, an oblique wave normal angle increases the advective pitch angle changes for kinetic energies of ~2.5 - 4 MeV and a wide range of pitch angles. In contrast, a linear polarization reduces the advective change over a wide range of kinetic energies and pitch angles. Second, phase space orbits, which are often time-dependent and mixture among phase trapping, untrapping and bunching effects, are sensitive to the wave normal angle, ellipticity, kinetic energy and pitch angle. Last, there is a kinetic energy and pitch angle range where the diffusion can become larger for a more oblique wave normal angle and smaller for a more noncircular (toward linear) polarization. Clearly it is critical to include accurate information of the wave normal angle and ellipticity in a realistic calculation of EMIC wave-driven electron scattering; Otherwise, a firm conclusion on the extent to which EMIC waves are responsible for relativistic electron precipitation is difficult to establish.

Fig. 8. (left panels) Advective and (right panels) diffusive pitch angle changes shown as a function of WNA for various cases of pitch angel and energy. WNA=wave normal angle. Adopted with slight modification from Lee et al. (2018).

Download Original Figure

5. POSSIBLE WAYS TO SCATTER NEAR-EQUATORIAL PITCH ANGLE ELECTRONS

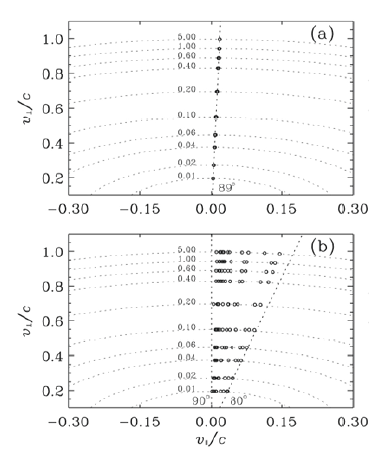
Most of the previous works indicate that EMIC waves alone hardly scatter near-equatorial pitch angle electrons, the population of which constitutes the majority of the outer radiation belt. Accordingly, some ideas have been put forward to resolve this issue. One of the ideas was given by Wang et al. (2016), who considered the Landau resonance for nearly equatorial electrons with oblique EMIC waves. For oblique EMIC waves, a parallel wave force is expected to exist, which should be responsible for the Landau resonance. Based on test particle calculations, they indeed found that nonlinear Landau resonance trapping can occur by oblique EMIC waves that scatter near-equatorial electrons (89°) to a lower pitch angle (~80°) in several seconds. They claimed that this can occur similarly for electrons for a broad energy (10 keV to 5 MeV), as demonstrated in Fig. 9. This result is meaningful considering that the cyclotron resonance does not work for 90° pitch angles.

Fig. 9. (a) The initial distribution of 12 electrons at each energy in the velocity space. (b) Final distribution of the particles after interaction with EMIC waves. Taken from Wang et al. (2016).

Download Original Figure

Another possible way to enhance large pitch angle scattering of relativistic electrons is to consider the combined effects of EMIC waves and other waves. In reality, drifting electrons may encounter multiple kinds of waves, not just one kind of wave. Shprits et al. (2009) suggested that scattering due to EMIC waves can cause a strong diffusion which enhances losses on the duskside. It consequently leads to a steep profile in the pitch angle distribution, which can assist chorus waves to scatter relativistic electrons into loss cone on the dawnside. Other waves such as hiss in plumes, magnetosonic waves, or low-frequency hiss (< 100 Hz) may be more efficient in such a combined scattering mechanism (Cao et al. 2017a,b;Meredith et al. 2006;Shprits 2016;Summers et al. 2008).

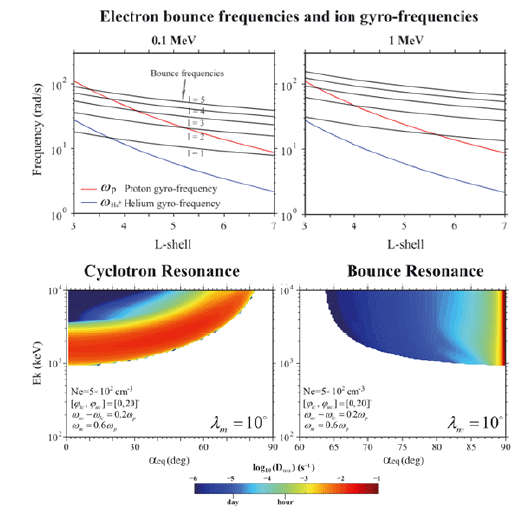
While most of the previous works considered a cyclotron resonant interaction of relativistic electrons, Cao et al. (2017a) considered bounce resonant scattering of radiation belt electrons by H⁺-band EMIC waves (Roberts & Schulz, 1968). The bounce resonance condition is given by ω=lω_b, where l is the resonance harmonic, ${\omega }_b=2\pi v/\left(4L{R}_E\tilde{T}\left({\alpha }_{eq}\right)\right)$ and $\tilde{T}\left({\alpha }_{eq}\right)=1.38-0.32\left(\text{sin}\hspace{0.33em}{\alpha }_{eq}+\sqrt{\text{sin}\hspace{0.33em}{\alpha }_{eq}}\right)$ (Schulz & Lanzerotti 1974;Shprits 2009;Chen et al. 2015;Li et al. 2015). In this resonance, H⁺-band EMIC waves can resonate with near-equatorially mirroring electrons over a wide range of L shells and energies, while He⁺-band waves can only resonate with electrons of < 100s keV in low-L shells. This can be seen in Fig. 10 (top panels), which shows the proton and He⁺ gyrofrequency curves and the 1st to 5th harmonics of the electron bounce frequency at 0.1 and 1 MeV. The resonance orders l = 1 to 5 imply the possibility for bounce-resonance of > 100 keV radiation belt electrons. Since an increase in electron energy will increase the corresponding bounce frequency, only the first three harmonics contribute to the pitch angle diffusion of relativistic (>1 MeV) electrons in the outer radiation belt. Using the method of Tao & Li (2016), Cao et al. (2017) computed the bounce-resonant pitch angle diffusion coefficients due to EMIC waves and compared the results with the diffusion coefficients from the cyclotron resonant interaction. The results in Fig. 10 (bottom panels) clearly indicate the difference in the pitch angle range where the bounce resonance and cyclotron resonant scattering effects are dominant. H⁺-band EMIC waves efficiently scatter electrons of >100 keV from ~90° pitch angles to more field-aligned pitch angles (with a strong L shell dependence), where the cyclotron resonance can further scatter electrons into the loss cone. Consequently, EMIC wave scattering becomes effective for a wider range of pitch angles than predicted from the cyclotron resonance only.

Fig. 10. (top) Proton and He⁺ gyrofrequencies and harmonics of the electron bounce frequencies as a function of the L shell. (bottom) Pitch angle diffusion coefficients due to the cyclotron resonance and bounce resonance with H⁺-band EMIC waves shown in the space defined by the electron energy Ek and equatorial pitch angle α_eq for L=4. Taken from Cao et al. (2017).

Download Original Figure

6. PRECIPITAION DUE TO RISING TONE EMISSIONS

Coherent EMC waves containing a series of rising tones have been observed by spacecraft in the magnetosphere (e.g., Pickett et al. 2010), and they are referred to as EMIC triggered emissions. Several papers have addressed the nonlinear pitch angle scattering of electrons by rising tone EMIC waves (Omura & Zhao 2012, 2013;Kubota et al. 2015;Kubota & Omura 2016). Theory by Omura & Zhao (2012) considered an electron interaction with a coherent L-mode EMIC wave propagating parallel to a static magnetic field for which the wave frequency was allowed to vary in time according to the following wave equation.

where V_g is the wave group velocity and z is the distance along the magnetic field line from the magnetic equator. The authors derived an approximate form for the second-order resonance condition, which is required due to the time varying (varying along the magnetic field line) frequency.

where ω_tr is a kind of wave trapping frequency of electrons, and S is the inhomogeneity factor that determines the resonant electron dynamics, which is a complicated function of the time variation of the wave frequency, inhomogeneity of background magnetic field, wave spectrum, electron energy and pitch angle. The efficiency of the resonant trapping is dependent on S. For S ≃ 0, most of the resonant electrons are trapped. For |S| > 1, trapping is not expected. In fact, S < 0, and for this condition, the trapped electrons are transported to smaller pitch angles as they pass through the wave packet.

A recent comprehensive test particle simulation by Kubota & Omura (2016) was applied to EMIC rising tone emissions present locally over 10° in longitude. The results indicated that nonlinear wave trapping first takes place for large pitch angles and then scatters some of the resonant electrons to smaller pitch angles, and some of them is further carried into the loss cone by scattering at a small pitch angle after being released from the wave trapping. The authors found that a significant number of electrons (mostly having ultrarelativistic energies) precipitated by EMIC waves on a time scale of several seconds, which they claimed would be much shorter than the time scale of quasilinear diffusion. However, the characteristics of electron precipitation differ for different kinetic energies and significantly depend on the wave frequency and the plasma density.

7. CONCLUDING REMARKS

The quasilinear resonant diffusion calculations carried out over the last 15 years have entered into a mature stage as a result of considering various aspects, such as the (partial) reflection of actual observations of EMIC wave properties, the MLT-dependent effect of scattering, kinetic dispersion effects compared to the cold plasma dispersion relation, distinctive roles among three bands of EMIC waves, the effects of background plasma and magnetic field, and the distinctive efficiencies of scattering by EMIC waves for subrelativistic, relativistic, and ultrarelativistic electrons.

The nonlinear and nonresonant effects that are missing in quasilinear resonant diffusion theory have also been considered in the efforts over the last 15 years and have been compared with the quasilinear calculations. Most of the effects have been studied by test particle simulations, which highlight the physics of nonlinear trapping, phase bunching, and advection. For a small-amplitude wave, the diffusion coefficients calculated by quasilinear theory and the test particle approach tend to agree, but the nonlinearity becomes important for a larger amplitude wave. Complicated nonlinear effects that have been identified from test particle simulations, as a whole, can affect the net pitch angle scattering rate differently from the predictions from quasilinear theory.

Other progress includes the consideration of effects due to oblique and noncircular waves on pitch angle scattering. This work highlights the strong necessity to implement a precise wave structure in realistic calculations of the pitch angle scattering and precipitation. In addition, oblique EMIC waves are important since they can scatter near-equatorial pitch angle electrons by the Landau resonance. Another suggestion to scatter near-equatorial pitch angle electrons is by a bounce resonance, in contrast to a cyclotron resonance. Studies on precipitation by rising tone EMIC waves have also constituted a great addition to the overall progress.

Despite this progress, it is clear that there still remains much work to be done. In this author’s opinion, the most serious issue is how to incorporate the actual EMIC wave observations into the theoretical and numerical calculations. Most of the previous works lack an accurate implementation of the observed EMIC wave spectrum for a specific event. In particular, we are not given precise information on the EMIC wave structure along the magnetic field lines along which electrons travel and interact with waves. The final, quantitatively reliable conclusions will be postponed until the field-aligned wave information is correctly implemented into the calculations.

Another meaningful topic to consider in future works is the consideration of the kinetic dispersion relation and its effect on the electron scattering, as few studies have been carried out on this subject so far. In addition, it is worthwhile to carry out a quantitatively extensive simulation of pitch angle scattering due to multiple waves, such as EMIC, chorus, and hiss waves. Although all of these waves together have been implemented in many of the quasilinear resonant diffusion simulations, the effects of each wave have been separately treated in calculations of the diffusion coefficients without considering the possible interplay between different wave scattering effects. Test particle simulations may be more appropriate to address the combined effects due to multiple waves that drifting electrons may encounter. The extent to which EMIC-wave-driven precipitation contributes to radiation belt electron dropout events remains to be determined quantitatively. Thus far, there have been more reports in the literature suggesting that EMIC waves alone may not be sufficient to explain the often observed major dropout events of relativistic electrons. EMIC-wave-driven precipitation may be effective for explaining ultrarelativisitc electron dropouts according to some reports; however, unanimous agreement has not yet been reached on this issue. One resolution may be to verify the proposed ways to scatter near-equatorial electrons by a bounce resonance, a Landau resonance, and multiple wave scattering together in a comprehensive way.