1 INTRODUCTION
When meteors penetrate the atmosphere, head echoes are typically produced along the pathway of the meteors, and nonspecular trails are left behind (Ceplecha et al. 1998; Dyrud et al. 2002). As such, meteors can be identified through these head echoes, which proceed downward and last for less than 1 sec (Sparks et al. 2010). Echoes can be observed from ionized plasma (nonspecular trail echo) produced through ablation, evaporation, and diffusion processes (Close et al. 2002). Meteor echoes in the summer polar mesosphere should be given more attention because meteor occurrence peaks during summer in the Arctic region (Younger et al. 2009; Jee et al. 2014). In addition, meteor smoke particles are involved in the phenomena of polar mesospheric summer echoes (PMSE) and polar mesospheric clouds (PMC) (Cho & Röttger 1997). Radar echoes can be detected from the formation of plasma irregularities in the atmosphere (Briggs 1950). At high latitudes, nonspecular meteor trails are known for being supported by field-aligned irregularities and charged meteor dust (Chau et al. 2014; Kwak et al. 2014; Yang et al. 2015).
Nonspecular echoes are also known as range-spread trail echoes (RSTE) (Chapin & Kudeki 1994; Zhou et al. 2001; Oppenheim et al. 2009) or spread meteor echoes (Reddi et al. 2002), and their formations have been explained using the Farley–Buneman gradient drift (FBGD) instability (Oppenheim et al. 2003; Dimant & Oppenheim 2009). Specular echoes can be observed when the radar beam direction is perpendicular to the ionized trail left behind a meteor (Ceplecha et al. 1998).
In this study, we report an unusual meteor trail that has a signature of moving along both vertically and horizontally straighten pathway with a varying the speed by 20–50 km/s following a long horizontal path of 24-29 km. The dynamics of plasma echoes were observed using spectrogram and radar interferometric analyses.
2 DATA ANALYSIS
Esrange mesosphere-stratosphere-troposphere (MST) radar (ESRAD) operates at a frequency of 52 MHz, i.e. a wavelength of 5.77 m, and is installed at Kiruna (67.8°N, 20.04°E), Sweden. ESRAD is set up with six-spaced receivers and antenna subarrays in two rows aligned to the W–E direction and three columns aligned to the N–S direction, so that receivers are arranged in west-to-east with a first row of 1, 2, 3 (north) and a second row of 6, 5, 4 (south). ESRAD points vertically with a beam width on transmission (1- way, full width half maximum) of 5°. If the whole antenna is used for reception, the 2-way beamwidth is reduced to 3.5° and the radial velocity is usually assumed as consisting of only the vertical component due to the atmospheric scatterer coming vertically from above. In the case of meteor echoes, the situation is slightly different. Meteor echoes are extremely strong, can have very high horizontal speeds and are almost never directly overhead. For more details of the radar and operating modes, see Kirkwood et al. (2007). Here we use the data measured in two modes. The first is the ‘met_300’ mode, using 1,072 Hz PRF with eight coherent integrations, giving 0.0075 sec time resolution, a height resolution of 300 m and height aliasing every 140 km with a base height of 60 km. Thus, met_300 mode can be used to observe meteors without suffering height aliasing, since meteoroid-produced echoes or head-echo-accompanied meteor trails usually occur at heights of 70–120 km.
ESRAD has an interferometric capability to resolve the spatial location of echoes (although with ambiguity for targets beyond zenith angles of about 10°) and the speed of growth of meteor trails. The signal received by the radar receiver is composed of complex numbers, giving amplitude and phase information. The angle (or phase) difference (δφ) of coherent signals acquired by two receivers gives information of the zenith angle of the scatterer (signal source) in the direction of the line connecting the receivers. Therefore the pattern of phase difference for each pixel of echoes in terms of time can provide the track of horizontal displacement with time. Phase difference for a signal received by two receivers can provide an arrival angle (θ) of the target using the formula (Skolnik 1962),
where λ = wavelength (5.77 m) and d is the distance between a pair of receivers aligned to the N-S or E-W direction (e.g., Rx5-Rx2: south-to-north arrangement, d = 32 m, or Rx5-Rx4: east-to-west arrangement, d = 24 m). At a range r, the offset from the radar zenith with respect to both E-W and N-S directions can be derived as,
where φE-W (δφN-S) is an averaged phase difference between pairs of receivers aligned to the E–W (N–S) direction (Skolnik 1962). The horizontal component of the moving distance (dx) between two points on a meteor trail can be obtained using
where Δoffset is the change in offset between the points.
The phase difference between receivers can be determined only with an uncertainty of the possible addition of 2nπ, where n is any integer, so the offets also have corresponding uncertainties, i.e. they may have an addition of r n λ/d. However, if r is changing slowly compared to the offsets, and n is the same from one point to the next, the Δoffset and dx will be insensitive to this ambiguity.
The height of the echo can be found from:
This will be sensitive to the 2nπ ambiguity and can be used to eliminate some possible values for n as they would result in meteors appearing to be at unrealistically low heights, or appearing to move upwards in time.
3 RESULTS
In this Section, we present an observation of meteor trail with respect to time and range. And also using phase difference between receivers, horizontal displacements are derived in terms of the x-and y-axes spatial domain, and heights of the meteor trail.
Figs. 1(a) and 1(b) show time–range morphologies of meteor echoes comprising the apparent head echo and the following noN-Specular or specular echoes, observed at Fig. 1(a) relative time from 6.2-10 sec Fig. 1(b) zoomed-in for strong echo for relative time from 6.2-7.7 sec observed at 01:30:39 UT on June 29, 2014. The echo power is represented as an average over six receivers of met_300 data. The relative time implies the time elapsed since the measurement started, for example, at 01:30:39 UT, as shown in Figs. 1(a) and 1(b).
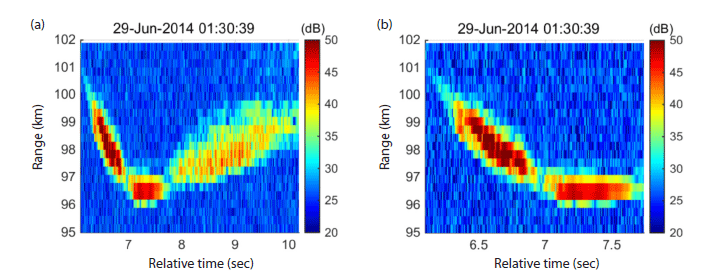
Echo power and phase can be derived from in-phase and quadrature components of the electrical signal received by the radar receiver at each range gate.
The range corresponding to the maximum echo power in the range spread (Fig. 1) at each time is used to track the position of the echo passing through with respect to time, as shown in Fig. 2(a). As shown in Fig. 2(b), echo power lines are drawn by tracing the maximum power at every sampling time. It can be noted that several peaks of power intensity are repeated during of the occurrence of the echoes.
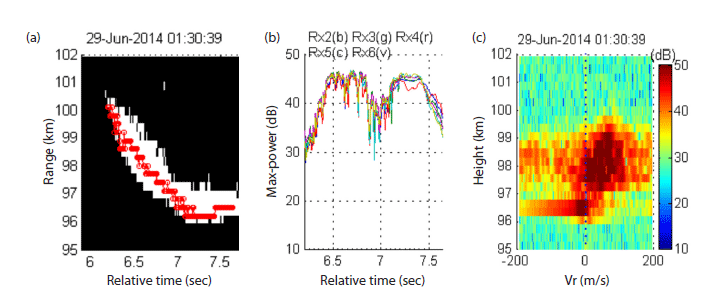
As shown in Fig. 2(c), the spread of Doppler velocity over time is derived from a spectrogram analysis of the meteor trails (time interval as shown in Fig. 1(b), respectively). Here, the spectrograms show that Doppler velocities (Fig. 2(c)) in general shift towards negative values with decreasing range gate. Echoes seem to be undergoing severe turbulence given the large spread of positive and negative radial velocities, coexisting in ranges of -191 to +192 m/s at most range gates with high spectral powers. There is some sign of narrower spectral width at the lowest heights. (Note that the velocity range is limited by a folding frequency according to the sampling rate, 0.0075 sec for met_300 mode).
The phase difference between receivers provides horizontal displacement with respect to each east-west (E–W) or north– south (N–S) alignment. In Figs. 3(a) and 3(b) range–time plots are shown for phase differences between channels aligned E–W (Rx2-3, Rx5-4, Rx6-5 and Rx1-2 (not shown)) and N–S (Rx2-5, Rx3-4 and Rx1-6), respectively. It is clear that a systematic change of phase difference occurs between each pair of receivers in each direction, continuously from the top to the bottom of the meteor echoes. This provides the basis for deriving a zero-order, unwrapped, phase-difference transition with respect to time. ‘Unwrapping’, i.e. the removal 2π steps to give as smooth as possible phase-changes over time, is combined with the assumption that the track passes through the radar main-beam (‘zero-order’). For the meteor, the results are shown in Fig. 3(c) (left) for E–W and Fig. 3(c) (right) for N–S directions.
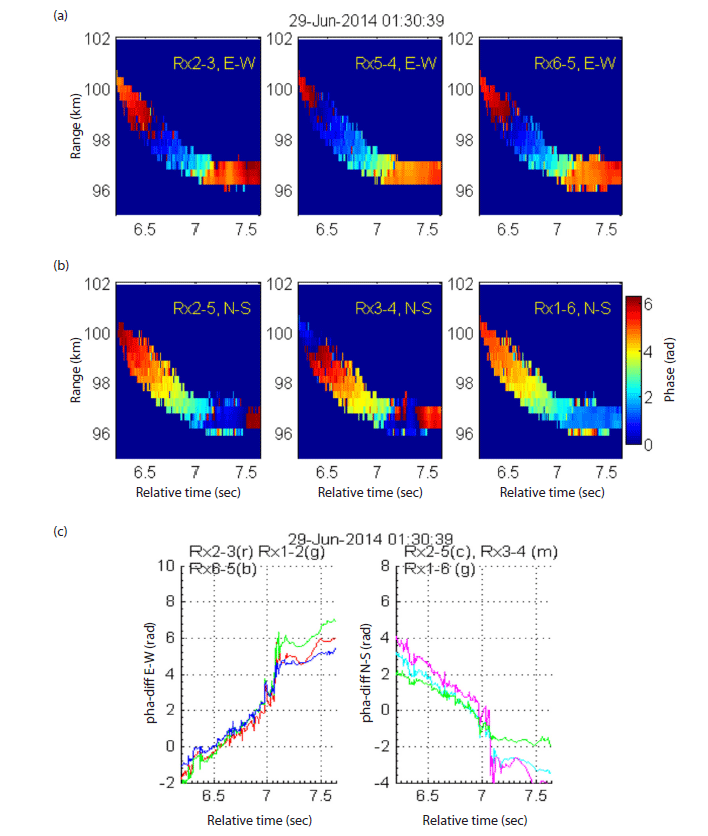
The continual increase (or decrease) of phase difference implies that the meteor trail follows a horizontal path not only doing vertical motion. The pathway of horizontal movement can be tracked by deriving the horizontal offset as referred to the radar zenith with respect to the E–W and N–S directions.
The ground diffraction pattern represents antenna response in power decreasing from the main lobe as shown in Fig. 4(a). Here, possible horizontal displacements according to radial distance from the radar is plotted in dashes on the ground diffraction pattern; Fig. 4(b) possible powers of the meteor trail is replotted in terms of x-offset; FIg. 4(c) possible height extensions of the meteor trail in terms of x-offset; Figs. 4(a)- 4(c) possible occurrences of the meteor trail above 75 km height are noted in black and blue, but those below 75 km are in omission or cyan.
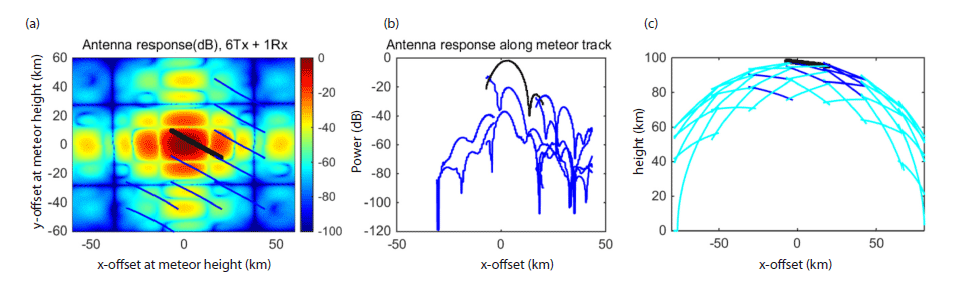
Zero-order, unwrapped phase difference is converted to horizontal displacements using Eq. (2), as shown in black thick line in Fig. 4(a). It should be remembered that the whole trail might, in principle, be displaced horizontally by r n λ /d, corresponding to integer multiples of ~24 km E-W, and/or ~18 km N-S at 100 km range (from the conversion of phase difference as in Fig. 3(c)). As referred to Fig. 4(c), however, most of possible values of n result in apparent heights below 80 km or the heights increasing in time. These unlikely occur for meteor trail. Only a few values of n remain reasonably possible, corresponding to horizontal translations of the track ~24 km east, or ~18 km north or south.
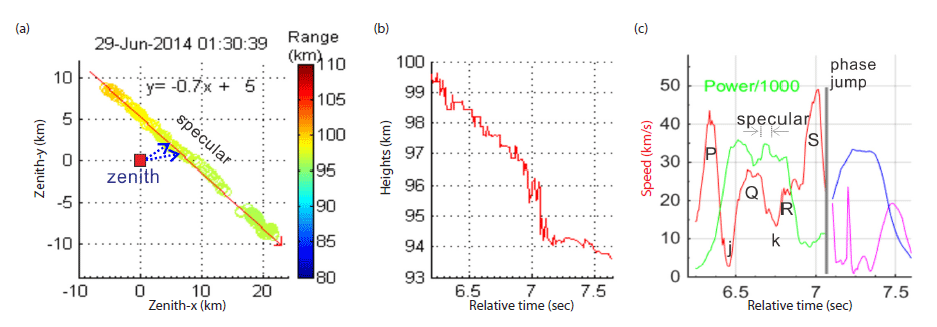
In Fig. 5(a), the scatterers’ transition described as radar zenith distance is marked by a sequence of circles in descending order from higher to lower range gates indicated by changing colors. The coordinates corresponding to echo locations are indicated with offsets (km) in x- and y-axes for E–W (positive for east) and N–S (positive for north), respectively. This implies that the meteor trail proceeds from northwest to southeast along a horizontally straight pathway. The pathway is fitted with a linear function of y = -0.7x + 5. A sudden jump in the track (offset jump) occurs near the end of the meteor trail (at a range of 96.5 km and a height of ~96.2 km (Fig. 5(b))). This is probably caused by the transition of different order of 2π. However, the offset jump is accompanied with a change of the character of the echoes in the spectral characteristics (Fig. 2(c)). The later echo trail extending in alignment to the previous slope as well as the strong echo power occurring in a time sequence (Fig. 1(a)) are not able to be explained with suggesting different sourced echoes. So as shown in Fig. 1(a), horizontal echoes (7.1-7.7 sec) are continued from the vertically slanted echo trail in penetration. Therefore, in Fig. 5(a) before and after the jump meteor trails stand aligned from one sourced meteoroid.
In Fig. 5(b), echo transit is plotted with respect to height and E-W offset. This shows that the meteor trail, if it is in the main beam, descends from 99.4 km down to 94.4 km, again along a straight pathway. If the trail is in an aliased position (displaced 18 km N-S, or 24 km E), the heights will be correspondingly lower, between 99 km and 85 km. However, as shown in Figs. 1(a) and 1(b) echoes at ~6.5 sec, 6.7 sec and 7.2-7.7 sec are really strong so that one of them could be induced by specular echo. As shown in Fig. 4(a) black trail echo (same with Fig. 5(a)) is only satisfied with the condition that one point in the trail becomes perpendicular to a line of sight and has a possible phase jump occurring near the end of meteor trail by a transition of diffraction region (or lobe).
As shown in Fig. 5(c), horizontal speeds of the meteor before (red) and after (magenta) the offset jump occurring are plotted. The speed is derived by employing a running mean in order to smooth any spiky noise. The running mean is operated with a window size of 13 samples. Here echo power development is plotted in non-logarithmic intensity (divided by 1,000) with respect to time, obtained by applying the running mean up to the offset jump (green) and including the jump (blue) over the same window size. Several peaks and troughs in speed are observed as the initial increase to (P) 40 km/s and decrease to very low at (j) 2 km/s, increasing again to (Q) 25 km/s and decreasing to (k), which is half the speed of Q. From the time point k, speed increases through two or three steps from (R) to (S), where speed after jump is not included. Assuming that the offset jump separates different echo targets, the speed curve (red) with excluding the jump does not completely drop down but remains high, at 25 km/s just before the time of the jump. In addition, at the same time, the echo power turns to on increasing. After the jump, speed also undergoes change, but lower than the previous levels, seemingly becoming slow down. As for echo power, a peak echo power occurs near 6.7 sec at which the closest (horizontally and vertically) distance of trail is achieved from the radar zenith (Fig. 5(a), red rectangle). The largest speed achieved after passing the closest point before jump suggests the meteor trail is not a simple head echo penetration but transferred to another kind of plasma wake, which can increase the speed itself and can increase the echo power at last. In Fig. 5(c), speed and power seems to some extent inversely proportional, but not to be given quantitive analysis. Echo power is largely enhanced after 7.08 sec, comparable to that produced by specular echo. Therefore, sudden release of plasma is expected, for example, explosive event. In addition, after completing its maneuvering through horizontal path, diffusive echoes are given out likely produced by atmospheric diffusion process from time of 7.7 sec (Fig. 1(a)) excluded for interferometric analysis due to meteor trail’s linear proceeding having been broken. This seems to provide a clue of the identification of echo trail.
4 DISCUSSION
The observed meteor trails are both characterized by apparently descending head echo with continuous changes in phase difference accompanied by strong turbulence. The changes in phase difference imply displacements along a straight pathway.
The observed meteor trails in this study make vertically declined and horizontally comparatively long extended transits. The total path lengths are at least 24 km before the occurrence of sudden offset jumps, and up to 29 km including the jump, as derived from horizontal displacements during the transit as shown in Fig. 5(a). The observation of the trail echo moving along a straight path with time implies that all the echoes are created by one meteor.
To compare the current observation with earlier studies, the structure and dynamics are considered in relation to head echoes, non-specular (or RSTE) echoes and specular (trail) echoes as follows. Firstly, the speed and duration before the jump occurring (speed 10 sec of km/s, trail duration ~1 sec, a small fraction of a second echo lifetime at each range) are similar to those reported for head echo in the similar radar frequency (Janches et al. 2014). However, it is distinguished from the traditional echo in that a set of observed trails mainly take horizontal traveling along a long pathway (24 km, versus 3 km vertical transition) with varying speed and reaccelerating speed in later times. In addition, after ending the vertical motion, it further proceeds a horizontal distance of ~5 km with re-enhancing echo power. This echo power is almost comparable to that produced by specular echo. So sudden release of plasma is expected including such as explosion. In addition, after completion of maneuvering horizontal path, it gives out diffusive echoes produced by atmospheric diffusion (Fig. 1(a)).
Secondly, the turbulent spectrograms might indicated RSTE as a result of FBGD instability, as have been reported in a number of studies in the literature (Chapin & Kudeki 1994; Zhou et al. 2001; Dyrud et al. 2002; Malhotra et al. 2007; Malhotra & Mathews 2009). When the radar is aligned perpendicular to the magnetic (B) field line, head and nonspecular echoes can be more frequently observed in a time sequence than when the radar beam is aligned acute or parallel to B field due to aspect sensitivity (Zhou et al. 2001; Malhotra et al. 2007). At Esrange, Kiruna, the inclination of B is about 78° so the radar beam is very far from perpendicular to the magnetic field and echoes from FBGD instability should be very hard to observe. The meteor trails observed in Figs. 1(a) and 1(b) are different from the normal RSTE in the way that the power increases and decreases more than once during the time they are on maneuvering. Similar increases in echo power have been demonstrated for a fireball explosion confirmed through camera observations by Park & McIntosh (1967). The traditional RSTE is raised by the remaining ionization after a head echo, lasting for a few seconds up to minutes while undergoing diffusion process. The observed meteor trail here shows strong turbulence throughout their lifetime with an almost horizontal transition along the horizontally straight pathway. This transition along the linear path cannot be explained with only the diffusion process in the atmosphere. In the meanwhile, after 7.7 sec, lower power echoes appear like a fume on increasing width and height in terms of time. Thirdly, we consider the possibility of specular (trail) echoes which are observed when a radar beam is perpendicular to an ionized trail left by a meteor. As mentioned above, the trail part at ~6.7 sec may be specular echoes perpendicular to a line of sight, since they occur at the closest points.
Variable transit speeds in meteor trail echoes do not seem to have been reported before. The meteor on 29 June 2014 exhibits acceleration of the speed from a drop below 20 km/s up to 45 km/s before the offset jump. Although nonspecular meteor trails observed by Sugar et al. (2010) or Oppenheim et al. (2009) were presented with receiver phase difference, the changes in phase difference were limited to the upper part of the descending trail and the echo power decays in the lower part. The transit speed (20–50 km/s) of the observed meteor trails exceeds the plasma drift velocity caused by FBGD instability (<100–300 m/s) by a large factor, and is also not attainable by background wind speed <100 m/s at ~90 km (Johnson & Killeen 1995; Sandford et al. 2010). Thus, the transit speed cannot be explained with the diffusion theory (Chau et al. 2014).
As a result, the observed meteor trail cannot be considered as the result of either a simple head echo or FBGD instability. The apparent head echo (the part before the jump) is in fact following several kilometers behind the meteoroid or the meteor trail is affected by an accelerating process, which leads to increases in echo power and turbulence, suggesting a new type of meteor echo with respect to both dynamics and structure. Similar meteor trails with speed increases were observed 2–3 times per day on average using the ESRAD radar during the summers of 2006 and 2008 (statistics for other periods are not yet available).
Based on the observation of apparently head echo-initiated plasma trail as shown in Figs. 1(a) and 1(b), meteors are likely the primary source of the fast-moving meteor trail. Accordingly, the candidates of the echo target are meteors, meteor fireballs, and meteor-triggered plasma phenomena.
Firstly, meteors have a speed in a range of 10–70 km/s with a maximum range of 20–40 km/s as observed using the MU radar, EISCAT and SKiYMET (Hocking 2000; Kero et al. 2013).
The speed range of the observed meteor trail is comparable to that of meteors. However, the majority of the kinetic energy of meteors is consumed during ablation such that they are obviously decelerated (Abe 2009). As such, the ablation of meteors and the increase in speed of the observed trail are not in agreement. And the speed of observed meteor trail is mainly contributed from horizontal transition (24 km long) rather than vertical motion (3 km long), different from usual meteor. Therefore, the observed increasing speed curve cannot be explained with the plasma directly surrounding a penetrating meteor.
Secondly, meteor fireballs usually have a speed range of about 10–25 km/s, which is lower than that of usual meteors; this is lower than but still similar to that of the observed meteor trails. The light curves of meteors/fireballs were found to show significant decreases before reaching the final spark (Spurný & Ceplecha 2008). The light curve for such fireballs might be considered comparable to the echo power curve observed in this study. Meteor fireballs may repeat the change in light intensity (Spurný & Ceplecha 2008) and probably transit along a straight pathway. It is noteworthy a diffusive echoes observed after strong echo occurring from 7.06-7.7 sec. Therefore, the strong echo can be explainable with sudden release of plasma from meteor fireball, explosive
Spurný & Ceplecha (2008) suggested that the passage of a meteoroid can cause charge separation between the meteoroid body itself and the plasma trail behind. The jet may be a type of electrical discharge running to the opposite polarity region at a distance, with that distance being somewhat variable over time. The phenomenon appears to be likely during summer in the polar mesosphere: strong vertical electric fields have been observed through rocket measurements (e.g., in NLC and PMSE layers, Zadorozhny et al. 1993; Holzworth & Goldberg 2004; Shimogawa & Holzworth 2009); horizontal supersonic neutral speed bursts (500–1,500 m/s) have been seen in PMC regions (Lee & Shepherd 2010) and extreme horizontal plasma drift speeds (300–1,400 m/s) occurring under highspeed solar wind streams in PMSE (Lee et al. 2014), were suggested as results of strong horizontal electric fields created in a local atmosphere. In this aspect, the observed meteor trail with almost horizontal transit with speed varying between 10–50 km/s is possibly initiated by meteor penetration and develops the secondary energetic phenomena in a type of fireball embedded with electrical property. Although from the radar interferometry analysis, horizontal path lengths are comparable to previous studies (e.g., Janches et al. 2013), meteor trails are characterized with varying transit speed of 10s of km/s apparently following several kilometers behind meteoroids and finalizing with intense echo power producing diffusive echoes, seem not to have been reported earlier.
5 SUMMARY AND CONCLUSIONS
In this study, one radar meteor trail is analyzed using echo power and phase difference between receiving antenna pair. Data were obtained using the Esrange MST (Meospshere– Stratosphere–Troposphere) radar (ESRAD) at Kiruna, Sweden. The observation can be summarized as follows. Consistent change in phase difference corresponds to continual shifts of horizontal displacements with respect to time, and to a signature of moving forward with considerable variations in speed, including acceleration process in later times. Spectrogram analysis showed that the meteor trail is accompanied with strong turbulence. The actual path of the meteor trail occurs along vertically and horizontally extended straight pathway, which is at most 28 km long, for meteor trail observed at 01:30:39 UT on June 29, 2014 (Figs. 1(a) and 1(b). Increases and decreases in speed without jump were detected during the descent of the trail. Small phase (or offset) jumps might have occurred under apparently constant increases in speed but could go undetected because the high speed exceeded the radar sampling frequency. The echo path resumed in the same straight pathway after the large jump.
The observed trails up to 7.7 sec are different in power structure and dynamics from previously reported head echoes and non-specular trails (or RSTE). The trails here have some similarities with meteor fireballs involving electrical property. Plasma discharges in the wake of fireball along the ~24 km and then 5 km horizontal distance could potentially explain the timing of the echoes and the variability of both power and speed in the trail. The identification of the observed meteor trail is still an open issue. Optical observation during daytime in the summer polar mesosphere and the lower thermosphere is required to gain better understanding of this new type of meteor trail.