1 INTRODUCTION
The Korea Pathfinder Lunar Orbiter (KPLO), the spacecraft for Korea’s first lunar exploration program, is being developed by the Korea Aerospace Research Institute (KARI) (Ju et al. 2013). KPLO will have a 100-km-altitude lunar polar orbit at the Moon for the nominal mission period. For successful mission operation of KPLO, the flight dynamics system (FDS) of the ground system has an important role. It is also the first FDS of Korea for future deep space exploration missions. Regarding KPLO FDS development, various studies have been conducted. Song et al. (2016) estimated the uncertainty requirements for orbit, attitude, and burn efficiency for a successful lunar orbit insertion maneuver using FDS. Bae et al. (2017) analyzed the burn delay of lunar orbit insertion of the FDS operation procedure. The early-phase contingency trajectory design for a failure of the lunar orbit insertion maneuver was also demonstrated for stable FDS operation (Song et al. 2017a). Deep-space navigation software was also developed to support the KPLO FDS implementation (Kim et al. 2017;Lee et al. 2017).
In the current development strategy, KARI FDS is designed using dual-engine concepts consisting of a commercial-off-the-shelf (COTS) engine and a KARI engine (Song et al. 2018). The COTS engine uses the Systems Tool Kit (STK) and Orbit Determination Tool Kit (ODTK) software by Analytical Graphics Inc. (AGI). The KARI engine employs in-house codes provided by the previous flight dynamics heritage of KARI. For orbit determination (OD), the COTS engine uses sequential filters, which have extended Kalman filter (EKF) and a backward smoother. Sequential estimation techniques such as EKF have the capability of rapid processing for mission operation. It conveniently supports OD with maneuvers. The KARI engine employs a batch least squares filter. The batch estimation algorithm delivers precise OD results for payload data post-processing, thus providing effective bias estimation. Song et al. (2014) summarized the lunar OD systems of the European Space Agency (ESA), Japan Aerospace Exploration Agency (JAXA), Indian Space Research Organization (ISRO), and China National Space Administration (CNSA), and reported the lessons from their experience. For stable performance implementation of the first space exploration trial, the COTS engine will be used as the primary navigation tool. The performance of the KARI engine will be validated by the KPLO mission, and then will be used as a primary engine for next lunar exploration mission of Korea. For the future, Korea will have its own deep-space navigation system. In this study, for the first step, a sequential estimation method was applied for KPLO OD using AGI’s ODTK.
The OD and orbit prediction (OP) are the main parts of space navigation. The performance of OD and OP are also critical for implementation of FDS functions. The strategies of OD and OP during mission operation affect the navigation performance for both the Earth-Moon cislunar and mission operation phases. The performance analysis of OD and OP is essential for mission planning and operation and payload science data processing. The observational arc length for OD is a significant factor in determining OD accuracy. The choice of the length of a tracking arc affects the performance of OD directly. The longer arc length can deliver more accurate OD results. However, the arc length for OD is limited by data processing time or maneuver schedules such as station-keeping and wheel-off loading. For effective mission operation, a proper arc length considering data processing schedule, mission operation procedure, and maneuver plans should be selected. From a practical viewpoint, the selection strategy of tracking arc length is an important tuning parameter to improve the accuracy of the orbit solution.
Various selection strategies of OD arc length have been applied in previous lunar missions. Because the OD requirements, dynamic modeling used, type of mission orbit, OD quality check method, and maneuver schedules also affect the performance of OD, we summarized only the arc length selection strategy instead of introducing OD accuracy for each mission. Beckman & Concha (1998) applied a 14-hr, 26-hr, and 55-hr arc length OD strategy for the Lunar Prospector (LP) mapping orbit. They changed the arc length for batch processing of OD for different lunar gravity solutions. For the higher-resolution gravity models, a 2-day arc was used for LP OD (Carranza et al. 1999). For ESA’s SMART-1 mission, the arc length for OD was changed from 2 days to 7 days because of the mission phase (Mackenzie et al. 2004). Goossens & Matsumoto (2007) demonstrated the OD results from LP tracking data and simulation data of SELENE using 2-day arc length processing.
The arc length for OD can be limited by spacecraft events such as maneuver and safe-hold mode. For China’s Chang’E-1 mission, one-day-based OD was utilized to avoid the effect of a momentum unloading maneuver (Jianguo et al. 2010). For SELENE OD, arc length was restricted by an angular momentum desaturation event to 12 hr for the main satellites, and one-week tracking data was used for sub-satellite OD (Goossens et al. 2011). Mazarico et al. (2012) selected 2.5-day tracking arcs for the Lunar Reconnaissance Orbiter (LRO) OD. The arc length was also varied from 1–1.5 days to 3.5–4 days because of events such as maneuvers or safe modes (Mazarico et al. 2018). The OD for the Chandrayaan-1 mission employed two different strategies, short arc and long arc (Vighnesam et al. 2016). The short-arc OD was used for the case of subsequent maneuvers within a short period. The arc length for Chandrayaan-1 OD was varied approximately 1 hr to 38 hr because of mission phase and tracking capability.
The effort to find optimal arc length for lunar orbiter OD has been made. The SPICE ephemeris by the NASA Goddard Space Flight Center (GSFC) Lunar Orbiter Laser Altimeter (LOLA) POD team used a 60-hr-based arc length for LRO OD (Nicholson et al. 2010). Maier & Baur (2016) analyzed the estimated orbit quality according to arc length for LRO OD. Arc lengths of 30 hr, 60 hr, and 108 hr were tested for the LRO OD optimal arc length candidate. The arc lengths of 2.5, 4.5, 6.5, 8.5, and 10.5 days were also attempted for OD analysis for LRO (Löcher & Kusche 2018). The 2.5-day (60-hr) arc strategy is known as the best and typical length for LRO OD when batch least square estimation is applied. For the GRAIL mission, 16–24 hr and 30–36 hr tracking arcs were applied for the edge-on and face-on period, respectively (Ryne et al. 2013). Wirnsberger et al. (2019) used an optimized strategy (max 2.5 days and 1.1 days on average) for LRO OD and gravity field recovery.
Most studies on lunar orbiter OD employ a batch estimation approach for tracking data processing. For sequential estimation using EKF, the arc length effect on lunar orbiter OD has less impact than the batch estimation case; however, the analysis of tracking arc length is needed for examination of effectiveness for stable mission operation including the accuracy of the orbit solution and tracking processing time. Slojkowski (2014) demonstrated that the sequential OD results using a dense 36-hr tracking arc have better accuracy than 60-hr arc length OD results by batch least squares estimation. Slojkowski et al. (2015) used a 24-hr forward filter and 48-hr or 96-hr backward smoother for LRO OD using ODTK software. For the LADEE mission, a sequential filter and smoother process was performed using a 3–5 day tracking arc for daily operational OD (Policastri et al. 2015a, b). For KPLO OD analysis, optimal arc length must be found for the batch and sequential estimation approaches.
In this study, for the KPLO nominal orbits, OD simulation using sequential estimation and performance validation by various arc length strategies were performed and their results were analyzed. We ignored maneuvers during the mission orbit phase, such as station-keeping for maintaining altitude and wheel-off loading for momentum unloading, because the schedule of KPLO maneuvers is not finalized. Instead, we included a short arc-length strategy for a frequent-maneuver schedule. For the preliminary performance examination of the KPLO FDS COTS engine, AGI’s STK/Astrogator 11 and ODTK 6 software were used for OD analysis.
Section 2 summarizes the measurement simulation procedure for OD, and Section 3 describes the OD strategy and arc length selection configuration. The initial configuration, modeling setting, estimation method, and accuracy validation strategy for OD are also summarized. Section 4 shows the results of an investigation of arc length effect on the KPLO OD. Additionally, OP accuracy assessment results are included for effective mission planning. Section 5 concludes this paper.
2 MEASUREMENT SIMULATION
For measurement simulation of KPLO OD, the true orbit of the mission operation phase was generated by using initial orbit elements. The inclination is 90° and the semi-major axis is 1837 km. Other elements were set to zero. This represents a lunar polar orbit that has a 100-km altitude. The orbital period at the epoch is 117.7 min. All Keplerian elements are represented by the Moon inertial coordinate frame. The simulated true orbit in a face-on view is illustrated in Fig. 1. The epoch of KPLO is set to 0 h (UTC) 1 August 2020. The motion of lunar-orbiting spacecraft is typically influenced by perturbing accelerations due to lunar and Earth gravity, solar radiation pressure, the third-body effect by planets in the solar system, and the general relativity effect. For a spacecraft in a lunar polar orbit at 100-km altitude, the most dominant perturbation is the lunar gravity effect. In this study, we employed most of these perturbations for describing the true orbit of KPLO. The dynamic modeling information used for true orbit generation is shown in Table 1. The GL0660B model was used for the Moon gravity effect with degree and order 660 by 660 (Konopliv et al. 2013). The solar radiation pressure and third-body effect by the Sun, Earth, and Jupiter were considered. The general relativity effect and radiation effect were applied. For numerical integration, Runge-Kutta 8-9 with variable steps was utilized.
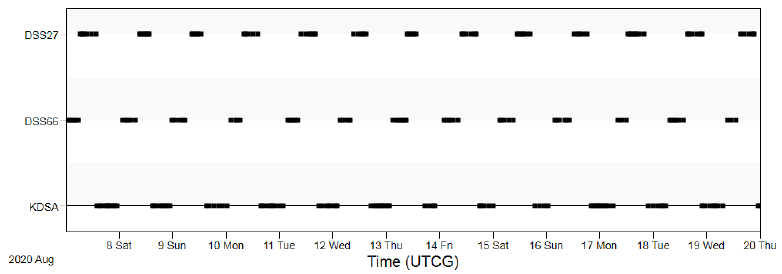
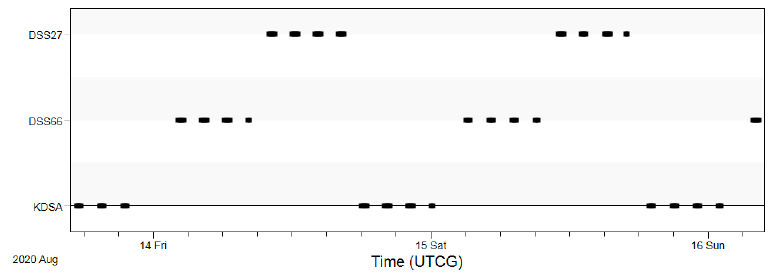
Total one-month measurements were generated by using a simulated true orbit and considered ground stations. The measurement interval was 10 sec and the duration of the tracking pass by ground station was limited to 30 min. This means that each station could secure tracking time up to 6 hr per day. For consideration of tracking restriction of a ground station, only one station can track KPLO in the overlapped period by more than two stations; therefore, the measurement simulation schedule of another station was excluded for the overlapped period. For KPLO tracking, two antennas of a deep space network (DSN), located at Goldstone and Madrid, and the Korea Deep Space Antenna (KDSA) were used. The configuration of ground stations for KPLO tracking is shown in Fig. 2. Because KDSA is under development, one of the candidate locations was used for the position of KDSA. For consideration of hardware characteristics, a specification document of KDSA was utilized in this study. The KDSA’s tracking schedule has high priority among the three stations for consideration of real KPLO mission operation. The pseudo-noise (PN) range and Doppler were employed for KPLO measurement simulation. Park & Moon (2018) analyzed the performance of both ranging techniques (sequential and PN ranging) for the KPLO space communication and demonstrated that PN ranging has better performance than sequential ranging for KPLO communication and operation. Figs. 3 and 4 show the tracking schedules of ground stations for the KPLO measurement simulation. We selected two antennas, Goldstone (DSS27) and Madrid (DSS66). Fig. 4 confirms that only a single station tracks the KPLO.
Measurement statistics including white noise sigma and transponder delay variation were considered for tracking simulation. The white noise levels of DSN measurements were set by the DSN service catalog, which describes range and S-band Doppler accuracies of 1 m and 0.2 mm/s, respectively (JPL 2015). Range and Doppler noise values of KDSA were assumed 10 m and 1 cm/s, respectively. Although the expected performance of KDSA is better than these values, we employed the larger values in consideration of the worst case. Transponder delay variation affects the range measurement performance of both DSN and KDSA; the maximum value of transponder delay variation was assumed approximately 12 m. Therefore, the final range noise values for DSN and KDSA were set to 13 m and 22 m, respectively. Doppler noise values for DSN and KDSA were set to 0.003 Hz and 0.15 Hz, respectively. The Doppler noise level of DSN applied the conventionally used values, which were converted to cycle-dimension (Hz) in ODTK software (Woodburn et al. 2015). The KDSA Doppler used noise values fivefold greater than those of DSN. The Gauss-Markov and random walk models were utilized for measurement bias and time bias estimation, respectively.
3 ORBIT DETERMINATION
For OD of KPLO, we employed ODTK 6 software with a sequential estimation algorithm using EKF and a fixed-pointer backward smoother (Vallado et al. 2010). In an actual operation situation, the COTS engine of KPLO FDS including ODTK software will be used. Therefore, OD analysis in this study is important for the preliminary performance investigation of KPLO FDS.
OD is the process of estimating the state vector by measurements and estimation algorithms. The dynamic model of OD integrates the equations of motion of a spacecraft using each measurement and predicts the state vector for the next time step. The measurement model prepares the calculated measurement values from the state vector of the spacecraft and position of ground stations. Measurement errors, such as troposphere and ionosphere delay, and measurement biases are also considered in the measurement modeling. The estimation technique iteratively updates the state vector to minimize the differences between the observed and computed values. The observational arc length of OD means the duration of tracking data utilized for estimating the state vector.
The equations of motion for lunar-orbiting spacecraft are described as follows:
where and are the position and velocity vectors, respectively, of the lunar orbiter. The values of G and M are the gravitational constant and the mass of the Moon, respectively. is the acceleration by perturbations such as gravitational and non-gravitational effects. The dynamic models for OD include the perturbation modeling for the calculation of all accelerations. Detailed descriptions of the dynamic models for OD are summarized in Table 1. The GL0660B lunar gravity model with a degree and order 100 by 100 was applied. For sequential orbit estimation of a 100-km-altitude lunar orbiter, it was shown that degree and order 70 by 70 provides balanced performance (Kim et al. 2018a). However, it was recommended to employ greater than 100 by 100 degree and order to maintain similar accuracy of orbit propagation (Song et al. 2017b). For the third-body effect, the Sun and Earth were selected to calculate perturbation. General relativity correction was not applied for OD dynamic modeling. For measurement modeling, troposphere and ionosphere delay correction, ground station plate motion and antenna correction, and measurement bias estimation were included in the process. For numerical integration, Runge-Kutta 7-8 with 30-s fixed steps was used. The differences between true orbit simulation and OD were intentionally made.
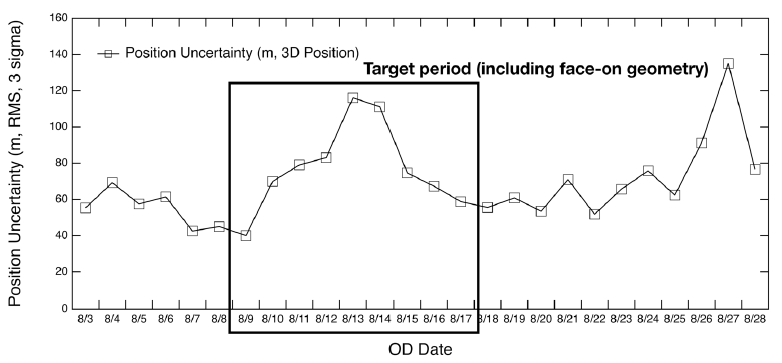
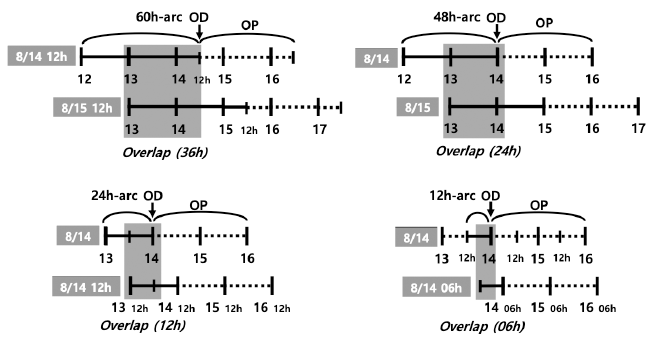
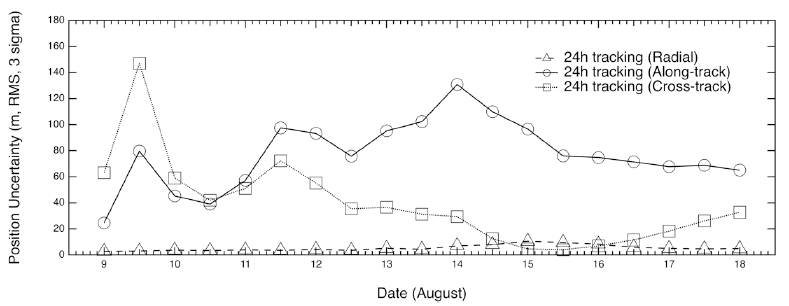
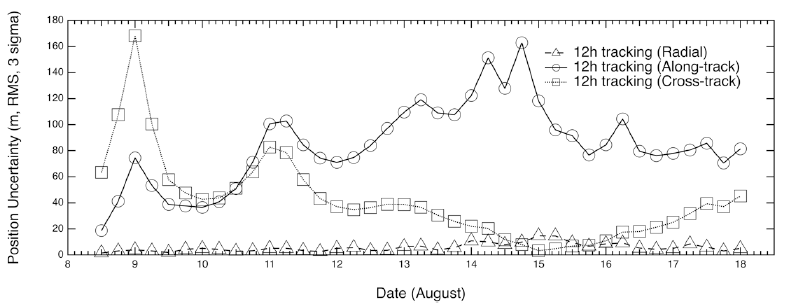
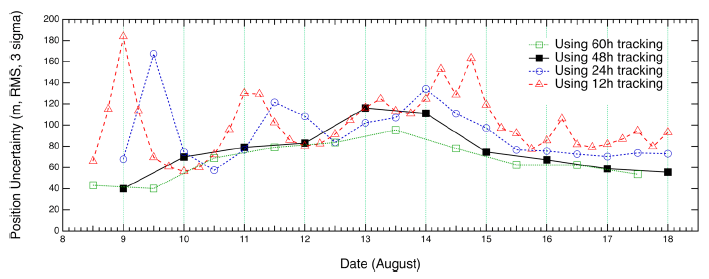
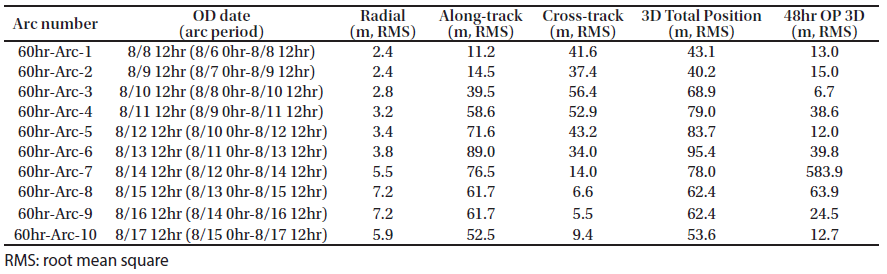
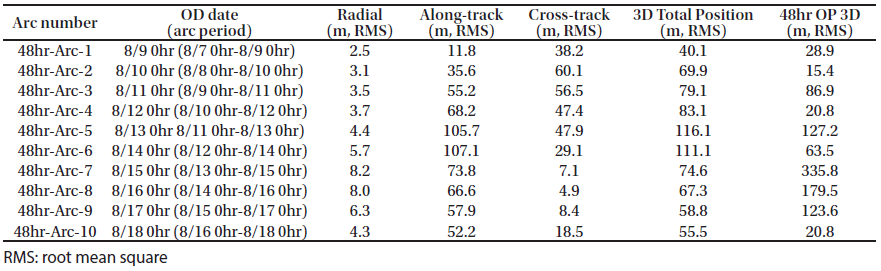
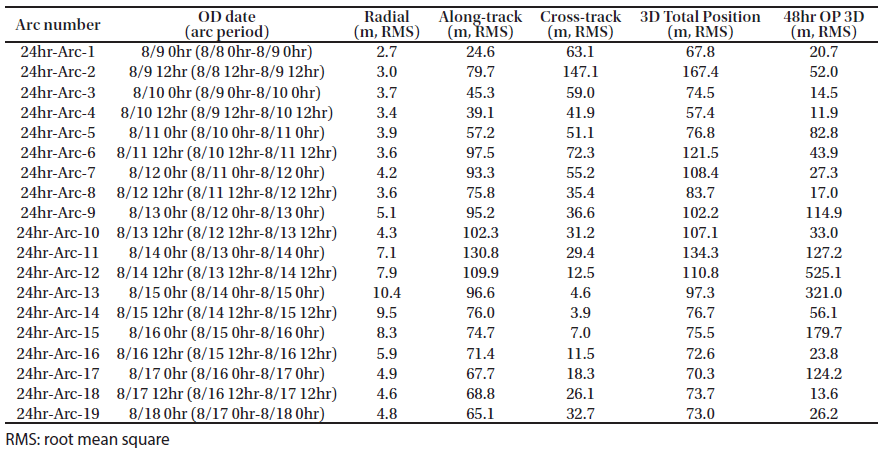
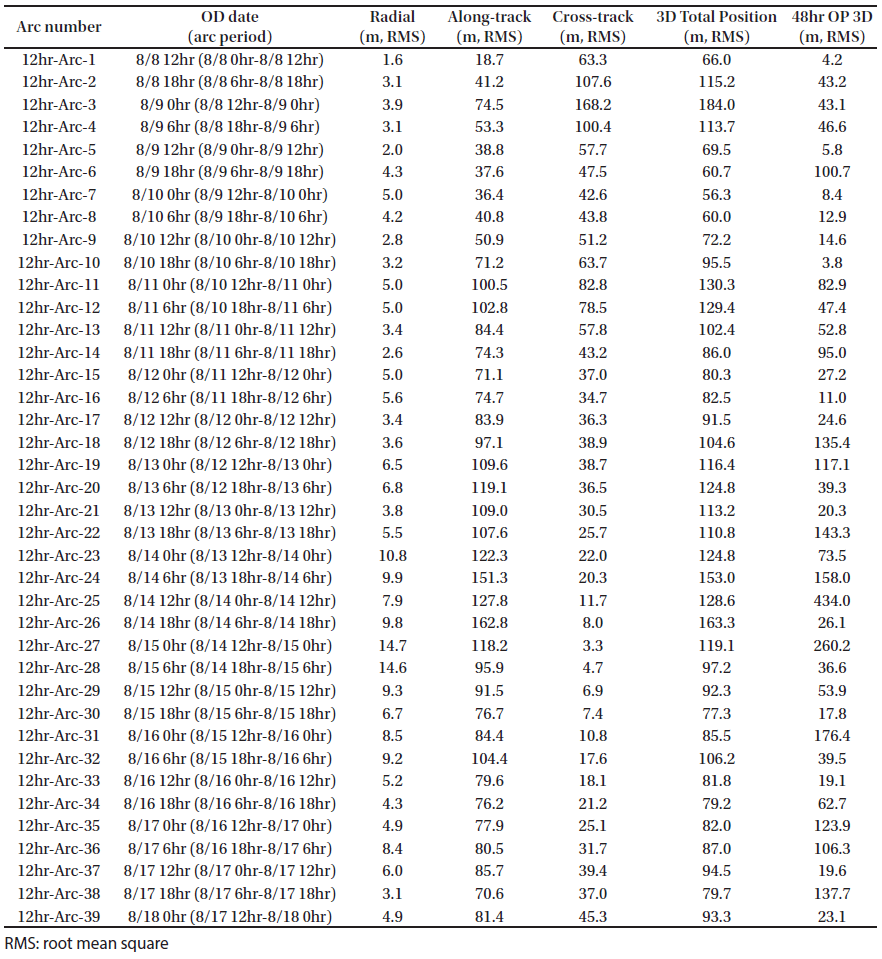
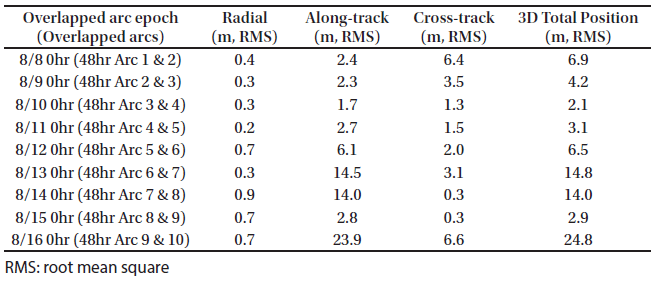
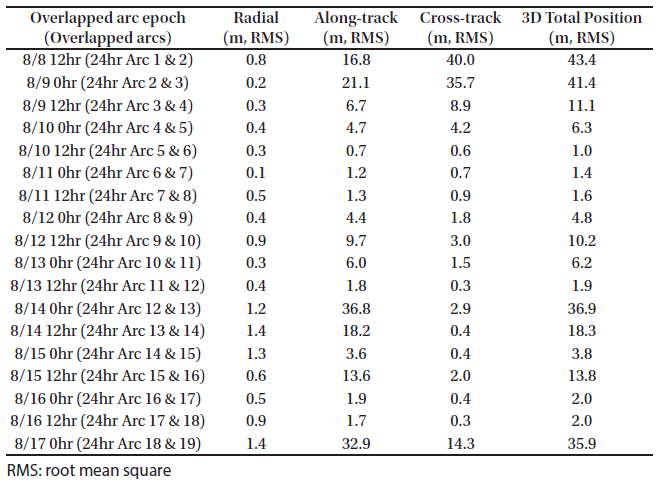
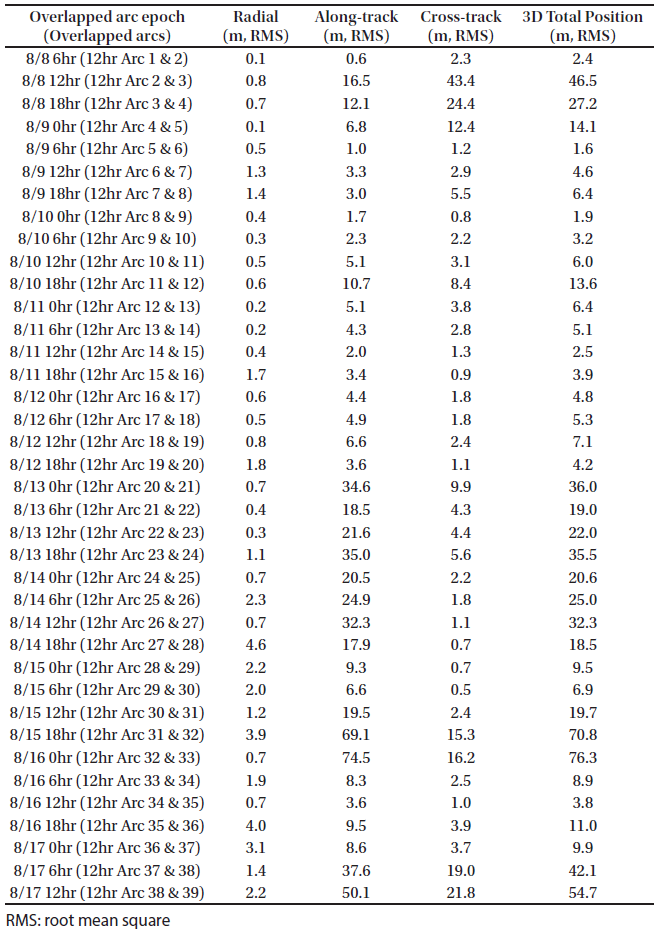
In this study, the basic OD strategy for KPLO was based on a daily schedule using a fixed arc length by three ground stations. Kim et al. (2018b) performed preliminary OD and OP analysis based on a 48-hr arc-length strategy during one month, which has total 26 arcs. In the consecutive daily 48-hr-based OD strategy, a 24-hr orbit overlap period was arranged for orbit precision assessment. We followed the same OD strategy of Kim et al. (2018b). Estimated parameters were spacecraft position and velocity, solar radiation pressure coefficient Cr, transponder bias, and measurement bias of each station. For the arc length effect on the OD investigation, we selected ten days (including face-on geometry) in the middle of the total one-month arc results of Kim et al. (2018b). “Face-on geometry” is the case where the line of sight from ground stations and the orbit plane of a lunar orbiter is perpendicular. In the face-on case, the observability of the radial and along-track directions is reduced because the orbit of the spacecraft is viewed as a circle. Therefore, the OD accuracies of the radial and along-track directions are degraded. On the other hand, edge-on geometry is the condition of the orbit seen as a line from ground stations; the cross-track observability becomes poor. Because the orbit error of a lunar orbiter has a more significant value in the along-track direction, the total 3D position accuracy of the face-on period becomes largest (Löcher & Kusche 2018). As shown in Fig. 5, the target period of this study includes the face-on geometry; therefore, we can examine the arc length effect on OD during the worst accuracy period. The arc length for OD was varied from 12 hr to 60 hr (12 hr, 24 hr, 48 hr, and 60 hr). In this study, we added the OP accuracy analysis based on various arc length OD results for stable mission planning. For OP, the orbit of KPLO during a total of 48 hr was generated by the same dynamic models used for OD. The epoch for OP was set as the end of the OD period. The arc configuration for OD and OP was designed as shown in Fig. 6. For the 60-hr and 48-hr arc length cases, a daily OD schedule was applied; however, for OD situations using 24-hr and 12-hr arc lengths, intervals of 12 and 6 hr, respectively, were used to establish overlapped arcs.
Initial orbit configuration for OD selects no direct orbit error condition, which means that we use the same orbit elements of a simulated true orbit. Instead, the initial orbit position error covariances were set to 200 m and 300 m for the radial/cross-track and along-track directions, respectively. Velocity error covariances were initiated to 3 cm/s and 2 cm/s for the radial and along-track/cross-track directions, respectively. The variation of initial orbit error generally also affects the accuracy of OD; however, we used a constant initial orbit uncertainty to focus on the arc length effect only. In this study, the iterative attempts for fine adjustment of estimation parameters were not considered. This means that the fine-tuning for OD accuracy improvement was not achieved. No fine-tuning strategy can examine the arc length effect on OD only.
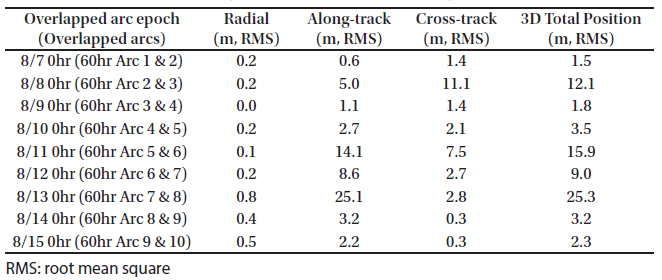
For OD quality assessments, position uncertainty by error covariance and orbit difference between two overlapped arcs were analyzed. For orbit overlap comparison, 6-hr, 12-hr, 24-hr, and 36-hr periods overlapped two arcs; therefore, two continuous arcs deliver one overlap performance. The overlapped arc configuration is described in Fig. 6. Orbit position differences by true orbit were utilized for OP accuracy evaluation. All uncertainties and differences are represented in the radial, along-track, and cross-track (RAC) directions and 3D total position using RAC information.
4 RESULTS
In this section, the results of OD and OP analysis are discussed. The OD for the one-month period using 48-hr arc-length tracking delivered the results of total position uncertainty under 140 m (3-sigma) and orbit overlaps precision under 35 m (Kim et al. 2018b). For OP analysis, Kim et al. (2018b) demonstrated that the performance of 72-hr OP with tuning was under 270 m. In this study, OD and OP performance variation by tracking arc length duration for 10 days was investigated.
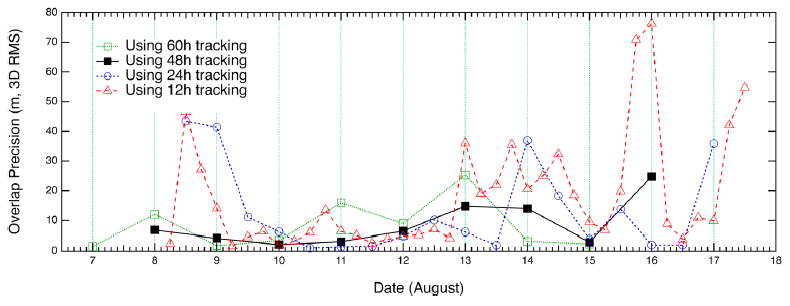
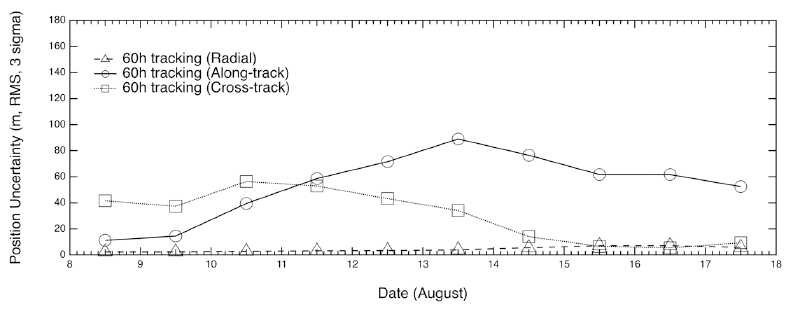
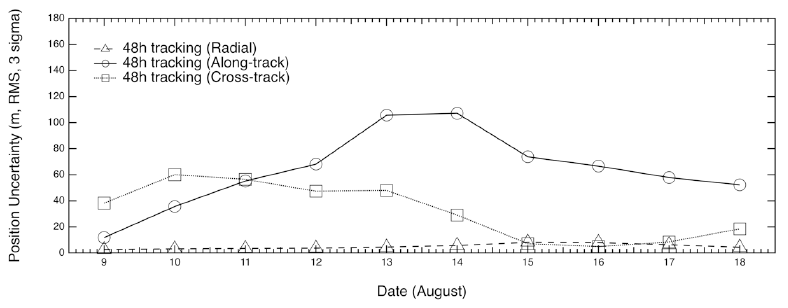
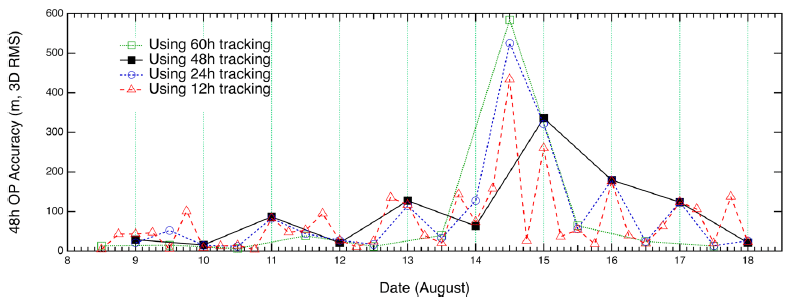
Figs. 7–10 show the position uncertainties by error covariance represented in each direction for OD using 60-hr, 48-hr, 24-hr, and 12-hr tracking arcs. The OD using 60-hr and 48-hr arc lengths employed a daily schedule. The 24-hr and 12-hr arc length cases performed OD every 12 and 6 hr, respectively. It was discovered that the OD precision in the radial direction yields better performance than the precision in the along-track and cross-track directions. The uncertainties of the along-track and cross-track directions have opposite trends because of the passing of the face-on Earth-Moon geometry. Fig. 11 shows the 3D total position uncertainty by error covariance using 60-hr, 48-hr, 24-hr, and 12-hr arc-length OD strategies. The results of the 12-hr arc-length strategy deliver the worst performance, and the 60-hr strategy shows the best performance. The differences between 48 hr and 60 hr are not significant. However, we found that the OD results using the 12-hr and 24-hr arc lengths deliver clearly degraded position uncertainties. Tables 2–5 show the RMS values of position uncertainties of all arcs for each arc-length case. Fig. 12 describes the orbit overlap precision using the 60-hr, 48-hr, 24-hr, and 12-hr arc-length cases. Tables 6–9 summarize the results of orbit overlap precision of all arcs for each arc-length case. The orbit precision of 12 hr and 24 hr delivers worse values than that of 48 hr and 60 hr. Orbit precision analyses by position uncertainty and orbit overlap difference demonstrate that the OD stability decreases for a shorter arc length than 48 hr. From the OD performance results considering both position uncertainty and orbit overlaps, we conclude that OD using more than 48-hr arc length delivers stable and acceptable OD precision. We also discovered that OD results using 12-hr and 24-hr arc length do not meet the KPLO OD requirement, which is a 3D position RMS value under 160 m (3-sigma) as shown in Table 10.
|
|
|
|
|
|
|
|
Fig. 13 shows the results of the 48-hr OP accuracy assessment by OD using 60-hr, 48-hr, 24-hr, and 12-hr arc lengths. The accuracy differences according to arc length are not as significant as those in the OD case. Because OD performance in this study is based on the sequential estimation technique, it is not sensitive to the OD accuracy of the entire arc but to the OD accuracy of the end of the arc. We can see that the 60-hr arc length strategy delivers the worst accuracy at the 8/14 12-hr epoch. The OP accuracy can be affected by the orbit element at epoch; therefore, a more sensitive strategy is needed to maintain stable OP accuracy. In this study, epoch tuning for OP was not accomplished to demonstrate the arc length effect only. However, for a real mission operation situation, the effect of OP epoch must be considered. The detailed values of the OP results are shown in Tables 2–5. The OP results summary is shown in Table 11. The worst case (8/14 12 hr) was excluded because of its irregular features.
In this study, the effect of arc length on KPLO OD using the sequential estimation technique was investigated. The arc length cannot be a critical factor for normal operation; however, abnormal situations or maneuver execution require quick and accurate OD performance. In this case, we require pre-analysis results to guide the selection of arc length and estimate processing time. From the viewpoint of contingency operation, the arc length effect on OD is an important and mandatory analysis item. Frequent maneuver execution can cause the situation of OD using a shorter arc length, and therefore OD analysis using short arcs is essential. The OD using a short arc length yields a more frequent operation schedule for orbit quality assessment by orbit overlap. If we select a shorter OD arc length than 24 hr, OD should be performed many times per day for stable orbit overlap analysis. This could be a significant burden to flight dynamic operators and analysts in mission operation. From a practical viewpoint, the short arc length sometimes means less ground support. It is more critical to reduce ground stations than decrease measurement numbers. Therefore, a 12-hr or 24-hr arc-length strategy can show more unstable OD performance than more extended arc-length OD. On the other hand, the limitation of ground station number affects the improvement of OD accuracy. Therefore, arc length greater than 48 hr cannot provide a remarkable enhancement. Meanwhile, it also means that arc length more than 48 hr, such as 60 hr, 7 days, or 14 days is not a useful strategy for the sequential estimation method. For batch estimation, the arc length effect can show another feature. We will examine the batch estimation case using the KARI FDS engine in the near future. The benefits of sequential OD are quick processing and accurate maneuver estimation. In particular, for translunar or lunar orbit insertion (LOI), station-keeping (SK) maneuvers, sequential estimation of OD has noticeably better performance. On the other hand, batch estimation provides the most accurate OD results using long arc and parameter adjustments.
5 CONCLUSIONS
In this study, KPLO OD and OP simulation using sequential estimation were performed, and the precision and the accuracy of OD and OP by various arc-length strategies were examined for the investigation of observational arc-length effect. A total of three ground stations (two DSN antennas and the KDSA) were utilized. To investigate the arc length effect on KPLO OD, 60-hr, 48-hr, 24-hr, and 12-hr tracking durations were applied. As a result, an OD strategy using greater than 48-hr tracking duration delivered results that meet the performance requirement, which is a position uncertainty by error covariance under 160 m (3-sigma) 3D position RMS value. The improvement by using longer tracking than 48 hr is not significant. Therefore, we concluded that a 48-hr arc length is suitable for KPLO mission operation. However, the OD analysis of 24-hr and 12-hr tracking duration is important for preparation of frequent-maneuver or contingency situations of mission operation. Additionally, OP performance analysis was accomplished, and the OP results demonstrated that the position difference between estimated orbits and simulated true orbits for 48-hr OP has accuracy at a level of 300 m. This study provides insight and guidelines for KPLO real mission operations in the nominal phase.