A Deep Space Orbit Determination Software: Overview and Event Prediction Capability

1. INTRODUCTION

For deep space exploration, deep space navigation tech-niques are essential. The deep space navigation process includes three major components: tracking spacecraft, orbit determination, and guidance operation. To track spacecraft in deep space, ground-based radiometric and onboard optical measurements are typically used. The deep space network (DSN) is the best-known ground station network providing radiometric tracking services. Onboard optical measurements may or may not be used for deep space navigation, depending on mission requirements. For instance, the Mars Pathfinder, Mars Climate Orbiter, and Mars Polar Lander only used radiometric tracking data for deep space navigation (Thornton & Border 2003). Orbit determination is a process for estimating the previous or current orbital state and spacecraft properties using tracking data. Based on the orbit determination results, guidance operations are applied to spacecraft to maintain or achieve the desired trajectory.

There have been efforts to develop deep space navigation software to support deep space missions using ground-based radiometric spacecraft tracking. Although government space agencies capable of deep space missions may have their own in-house deep space navigation software packages, there are few deep space navigation software packages available or purchasable for the general public. General Mission Analysis Tool (GMAT) is an open-source software package developed by the Goddard Space Flight Center (GSFC) and collaborators, and GMAT has an external navigation plugin including the DSN two-way range, Doppler observation models, and a batch least squares estimator (Hughes et al. 2017). The GSFC is planning to replace the legacy software package GTDS with GMAT, and the first target is to operate the SOHO mission with GMAT in the near future (Hughes et al. 2017). MONTE is a commercial software package developed by the Jet Propulsion Laboratory (JPL). MONTE is based on the JPL’s legacy software packages DPTRAJ and ODP, and has served all of JPL’s deep space missions, such as Cassini and Gravity Recovery And Interior Laboratory (GRAIL), since 2012 (JPL 2017). The orbit determination tool kit (OTDK) is a commercial software package developed by Analytical Graphics Inc., and has been successfully applied to the Lunar Atmosphere and Dust Environment Explorer (LADEE) mission along with the company’s other software package, Systems Tool Kit (STK) (D’Ortenzio et al. 2015).

There are pros and cons of using commercial or open-source deep space navigation software to support a deep space mission. Using commercial or open-source deep space navigation software can save time and efforts compared to developing and maintaining mission-specific deep space navigation software. Sometimes, using external navigation software can be cost-effective compared to developing mission-specific navigation software when there is no legacy software to refer to for the development. Conversely, the usage of commercial or open-source deep space navigation software is not always acceptable, depending on mission requirements and specifications. For instance, the current version of GMAT does not support prediction of solar outage but predicting solar outage may provide necessary support to a deep space mission in certain situations. In addition, the specific software input and/or output interface may differ from desirable interface specifications. Thus, using commercial or open-source deep space navigation software can be a good option, if the mission requirements and interface specifications are well supported by affordable software packages. However, where this is not the case, it is necessary to develop mission-specific deep space navigation software.

This paper introduces deep space orbit determination software (DSODS), which is a Mathworkf’s MATLAB object-oriented programming environment-based navigation software for deep space missions developed by Yonsei University in collaboration with the Korean Aerospace Research Institute (KARI) to support the Korea Pathfinder Lunar Orbiter (KPLO) mission. DSODS has three major capabilities: celestial event prediction for spacecraft, orbit determination with DSN tracking data, and DSN tracking data simulation. DSODS satisfies the current functionality requirements of the KPLO mission regarding orbit determination, data simulation, and event prediction, and will support the related interface specifications for the KPLO. This paper addresses only the validation and verification of event prediction capability. Its orbit determination and tracking data simulation capabilities are validated and verified for lunar missions based on processing and analysis of the flight data of Lunar Prospector, which was one of the National Aeronautics and Space Administration (NASA) Discovery missions (Kim et al. 2017a, b;Lee et al. 2017).

There are two goals of this paper: introducing an overview of DSODS and addressing event prediction capabilities in terms of how they work and their validation and verification. Three main drivers affected the overall design of the DSODS: compatibility with GMAT, the interfaces between modules, and the input and output data specifications. The compatibility with GMAT was important because the orbit propagation (OP) module now utilizes GMAT as a third-party software component, and GMAT has been in charge of handling fundamental astrodynamics-related operations. This decision has significantly shortened the overall development period of DSODS, and minimized the efforts spent on the development and testing of the OP module. However, a drawback of using large third-party software such as GMAT is that the limitations of GMAT are the same as those of DSODS. For instance, currently, GMAT and DSODS only support gravitational potential data with a degree and order equal to or less than 165. To mitigate such limitations, all GMAT dependent components are located in the OP module and isolated from event prediction (EP), data simulation (DS), and orbit determination (OD) modules. Thus, only the OP module needs to be modified to replace GMAT with another third-party software, if necessary.

The EP module determines the locations of events in the time domain based on a geometrical approach (Parker & Hughes 2011). Currently, the EP module satisfies the functionality requirements of the KPLO (Song et al. 2016), and is expected to satisfy the future performance requirements of the KPLO. The EP module consists of three major components: event functions, an analytical event location algorithm, and a mesh-refinement algorithm. An event function is defined as when a corresponding type of event (e.g., eclipse) occurs, the value of the event function is always equal to zero. From such a definition, it is clear that finding the roots of the event function is equivalent to locating the event. To find the roots of the event function, the analytical event location algorithm utilizes a cubic Hermite spline and analytical roots of the cubic equation. The merit of the analytical event location algorithm is that it does not require an iterative process to locate the roots. For accuracy control of the event prediction results, a mesh-refinement algorithm is applied to the EP module because event prediction accuracy is dependent on the event function data-sampling rate. The mesh-refinement algorithm estimates the relative errors between the event prediction solutions from two different sampling rates, and applies increased sampling rates in the intervals where the relative errors do not satisfy the user-defined tolerance. To validate and verify the event prediction capabilities of DSODS, a carefully selected set of test problems is implemented according to the functionality requirements, and the external truth data are generated using flight-proven software packages such as Spacecraft Planet Instrument C-matrix Events (SPICE), STK, and GMAT.

In Section 2, a brief explanation of the Common Utility and Class Library (CUCL) and the highest-level data flows for event prediction, orbit determination, and tracking data simulation are presented. Sections 3 and 4 address OP and EP modules in light of their responsibilities and how they work, respectively. In addition, Section 4 includes the validation and verification results on the DSODS event prediction capabilities. In Section 5, the summary and conclusions of this study are presented.

2. DSODS OVERVIEW

This section presents an overview on some important features of DSODS including the user environment, CUCL, and representative examples on its major applications with key data flows. Now, DSODS supports a script-based user interface, and is executable with a MATLAB 32-bit version higher than 2013b under Microsoft’s Windows OS environment. Such limitations exist for two reasons. First, DSODS was developed based on MATLAB object-oriented programming, and the MATLAB object-oriented programming environment is rapidly changing due to its active development. Second, DSODS includes some 32-bit MATLAB executable files to improve execution speed, and to interface GMAT because GMAT is a 32-bit application mainly written in C++ with some legacy FORTRAN components. Note that GMAT has been used for fundamental astrodynamics-related operations as a third-party component. The details of the MATLAB-executable (MEX) based GMAT interface is introduced in Section 3.

DSODS consists of one library named CUCL, and four modules: OP, EP, DS, and OD modules. The CUCL includes common utilities and fundamental classes used by multiple modules such as the epoch time, coordinate, ephemeris, spacecraft, and ground station classes, etc. The OP module is responsible for fundamental astrodynamics operations such as time and coordinate system conversions, orbit propagation of spacecraft orbit, and providing ephemerides of celestial bodies. The EP module is responsible for predicting celestial events such as eclipses, apsis passages, node crossings, solar communication interferences, and ground station visibilities. The DS and OD modules are closely tied, and responsible for orbit determination of spacecraft and tracking data simulation. The DS module includes the DSN sequential range and Doppler observation models, their noise characteristics, and media and antenna correction models. Using the DS module, the OD module conducts orbit determination with DSN tracking data files written in tracking data message (TDM) format, which is an international tracking data format standard defined by the Consultative Committee For Space Data Systems (CCSDS). The OD module generates pseudo DSN tracking data written in the TDM format. In the OD module, a batch least squares estimation algorithm has been implemented to solve the orbit determination problem (Cappellari et al. 1976). In addition, the OD module provides covariance analysis methods such as covariance propagation, projection, and transformation.

Fig. 1(a) shows the highest-level data flow of the DSODS event prediction process. The user or OD module can make an event prediction request for the EP module with the spacecraft ephemeris, ground station list, and/or list of occulting bodies (i.e., the Moon), as well as relevant settings. To generate the spacecraft ephemeris, it is possible to utilize the OP module, but the EP module cannot distinguish whether the spacecraft ephemeris is generated by the OP module or other tools such as STK and GMAT, as long as the ephemeris is written in STK’s ephemeris or CCSDS OEM format. If needed, the EP module obtains ground station (GS) and/or celestial body (CB) ephemerides using the OP module. Using the ephemerides of spacecraft (SC), GS, and/or CB, the EP module locates the desired events in the time domains, and delivers the event prediction results to the user or OD module. There are two possible forms of event prediction results: a text-based event prediction report and instances of Event Prediction class, which are discussed in Section 4.

Fig. 1. Data flow diagrams for: (a) event prediction, (b) orbit determination, and (c) data simulation.

Download Original Figure

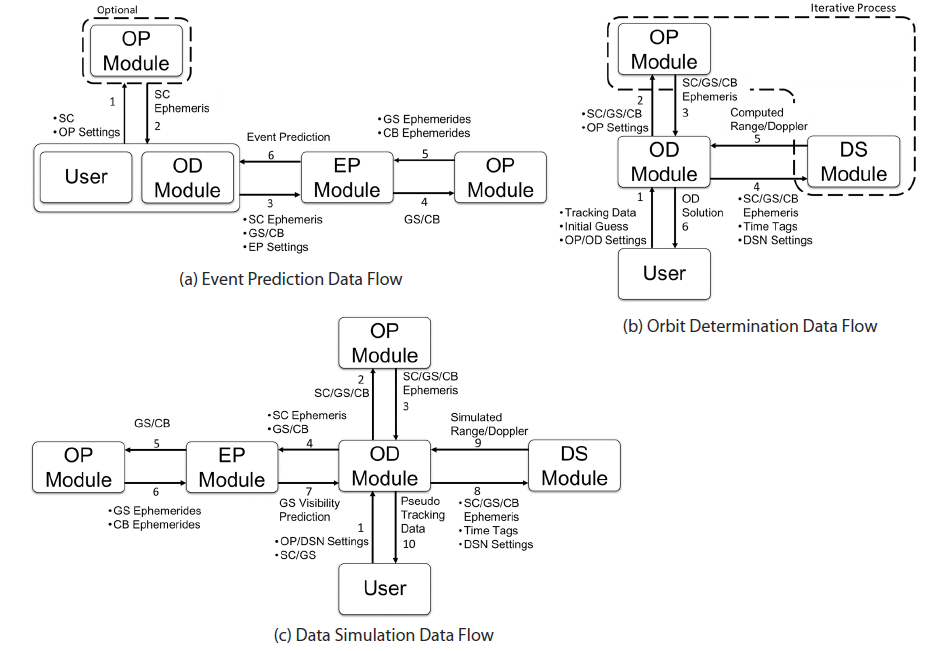
Fig. 1(b) shows the highest-level data flow of the DSODS orbit determination process. The user can make an orbit determination request from the OD module with an initial guess on solve-for parameters (e.g. the initial state vector of the spacecraft, the spacecraft solar radiation pressure (SRP) area, and range/Doppler biases), spacecraft, spacecraft tracking data in CCSDS TDM format, and relevant settings. Based on the user’s input data, the OD module conducts orbit determination with a weighted batch least squares estimation algorithm (Cappellari et al. 1976). Tracking data includes information on the ground station, DSN measurement settings for range and Doppler observables, DSN measurements, and time tags of measurements. Note that all the range and Doppler observations include radio signal integration over the time interval, and a time tag represents the measurement time. The OD module obtains ephemerides of the spacecraft, ground stations, and celestial bodies using the OP module with the spacecraft, ground stations, and relevant settings. Then, the OD module acquires the computed range and Doppler observables using the DS module with the ephemerides and relevant settings. The OD module then calculates the residuals between the computed and observed DSN measurements so that the OD module updates solve-for parameters to reduce the weighted least squares of residuals. If solve-for parameters are converged, the OD module delivers the orbit determination solution to the user. Otherwise, the OD module continues updating solve-for parameters until solve-for parameters converge or the number of iterations reaches the predefined maximum iteration number. As a result, the OD module produces a readable report in the DSODS format. The OD report includes information on the solve-for parameter solution, the covariance of the OD solution, measurement residuals, the measurement data editing history, DSN settings, and orbit propagation settings.

Fig. 1(c) shows the highest-level data flow of the DSODS tracking data simulation process. The user can make a DSN measurement data simulation request to the OD module with the truth data for solve-for parameters (e.g. initial state vector of spacecraft, spacecraft SRP area, and range/Doppler biases), spacecraft, ground stations, and relevant settings.

Using the DS and EP modules, the OD module creates a set of simulated range and/or Doppler measurements, and saves it in a text file written in the CCSDS TDM format. Compared to event prediction and orbit determination processes, the tracking data simulation process includes the majority of event prediction and orbit determination processes, except the iterative process. In addition, in the tracking data simulation process, the DS module does not produce computed range and Doppler observables but simulated sequential range and Doppler observables, which include simulated white noise and user-defined biases.

3. OP MODULE

The OP module is responsible for fundamental astro-dynamics-related operations: orbit propagation, time and coordinate system conversions, and creation of spacecraft and celestial body ephemerides. Currently, the OP module utilizes the GMAT as a third-party software component, and the GMAT is in charge of handling these fundamental operations. For mathematical details, see the GMAT mathematical specification document (GMAT 2017). Although using the GMAT has significantly shortened the overall development period of DSODS, the capability and application environment of the OP module is limited by the GMAT. For instance, currently, the GMAT supports only gravitational potential data with a degree and order equal to or less than 165. In addition, the user needs a MATLAB 32-bit version higher than 2013b to run DSODS under the Microsoft Windows OS environment. However, the OP module includes all the GMAT dependent codes so that the other modules cannot distinguish whether the OP module is using the GMAT or not. Such GMAT dependency isolation was intended to make the GMAT replaceable with other third-party software in the future.

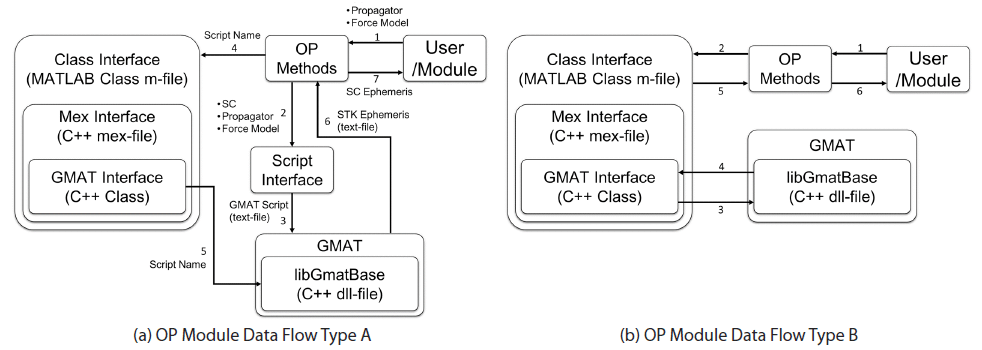
The OP module consists of module-level methods, the MATLAB/GMAT interface, and public classes. Table 1 explains the module-level methods provided by the OP module. These module-level methods are used by the other modules throughout DSODS. Table 2 introduces the components of the MATLAB/GMAT interface with brief explanations. There are six components: script interface, class interface, MEX interface, GMAT interface, GMAT base library (libGmatBase.dll), and GMAT data files. Note that these components are either binaries or classes written in MATLAB or C++. Finally, there are four public classes accessible by any module: the air-drag model, the gravity potential model, the force model, and the propagator. These classes are used to deliver orbit propagation options, and are compatible with but not dependent on the GMAT. Using these public classes, the script interface class writes a GMAT script that gives an order to the GMAT regarding how to propagate the spacecraft trajectory.

Table 1. OP module method list

Download Excel Table

Table 2. MATLAB/GMAT interface component list

Download Excel Table

Fig. 2 shows the two data flow diagrams of the OP module. Fig. 2(a) is the data flow diagram for orbit propagation, which shows that the class interface cannot directly access the GMAT base library (libGmatBase.dll) but contains the MEX interface, which can communicate with the GMAT base library. Note that for orbit propagation, most of the data communication is indirect and based on text file access, except for the name of the script, which is a string type data, and is directly delivered to the GMAT base library through the MEX interface. Moreover, Fig. 2(b) presents the data flows of the other operations such as time and coordinate system conversions and ephemeris generations of ground stations and celestial bodies. The specific data contents are omitted in the data flow diagram because they are dependent on the operation (or, method) being applied. Note that, in this case, all data communication is direct and based on memory access so that type casting between MATLAB and GMAT data types is required. The GMAT uses an internal Rvector array type while the MEX interface uses its own mxArray type, where non-standard C++ type identifiers are denoted in italics. Thus, the MEX interface converts Rvector to mxArray and vice versa using the standard C++ type array.

Fig. 2. OP module data flow diagram: (a) type A for orbit propagation and (b) type B for other operations.

Download Original Figure

4. EP MODULE

The EP module predicts astrodynamics-related events, and delivers information on the timing and type of event to the user or the OD module to aid the mission planning and design process. The highest-level data flow diagram is provided in Fig. 1(a). The EP module addresses various types of events such as orbital status, eclipses, ground station visibility, and solar communication outages. However, the current implementation of the EP module does not consider special relativistic light time delay and stellar aberration. The EP module was developed to support the KPLO and, in the Earth-Luna system, perturbation effects usually cause errors of less than a few seconds. Future extension of the EP module may include these perturbation effects for applications to other deep space missions beyond the Earth-Luna system.

The EP module consists of event functions, an event location algorithm, a mesh-refinement algorithm, and public classes. The event functions are defined for different types of event in that when an event occurs, the event function value is equal to zero. For instance, Eq. (8) is an event function for solar communication outage. As a result, finding roots of the event function is equivalent to locating the events. The event location algorithm finds the location and type of events by solving the root-finding problem with the data provided (i.e., event function and ephemerides of spacecraft, ground stations, and celestial bodies). To find the roots of the event function, the event location algorithm utilizes the cubic Hermite spline and analytical roots of the cubic equation. The mesh-refinement algorithm estimates the quality of the event prediction solution and updates the mesh-points used in the root-finding so that the quality of the event prediction solution satisfies the user-defined tolerance. There are two public classes in the EP module: point-type event prediction and interval-type event prediction classes. These classes contain information on the location and type of events obtained by the event location algorithm.

4.1 Functionality Requirements

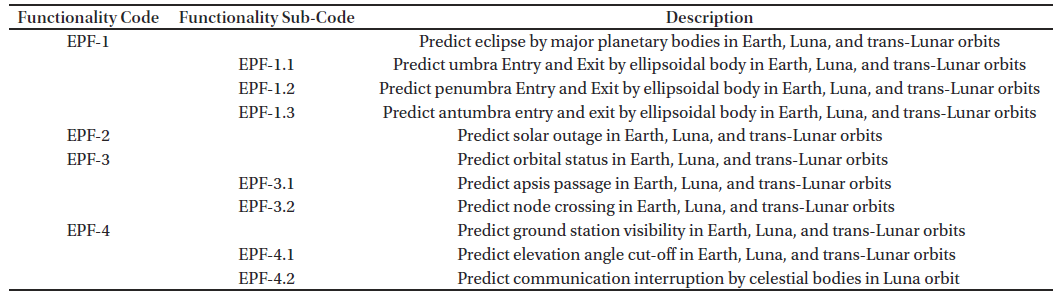
The current list of event prediction functionality require-ments for the KPLO is presented in Table 3 (Song et al. 2016). Each functionality code (i.e., EPF-1) indicates a category of the functionality requirement. If necessary, a functionality code can be divided into multiple functionality sub-codes (i.e., EPF-1.1, EPF-1.2, and EPF-1.3) because an event may be determined by multiple geometrical configurations. For instance, ground station visibility is acquired only when the elevation of the spacecraft is higher than the cut-off angle of the ground station and the signal is not occulted by any celestial body. Although functionality codes appear fairly fixed, new functionality sub-codes can be added in the future. For instance, EPF-3, which is an orbital status event, is expected to have more minor functionality codes than at present because the KPLO’s detailed mission requirements are still to be determined.

Table 3. Event prediction functionality requirements for KPLO

Download Excel Table

4.2 Event Location Process

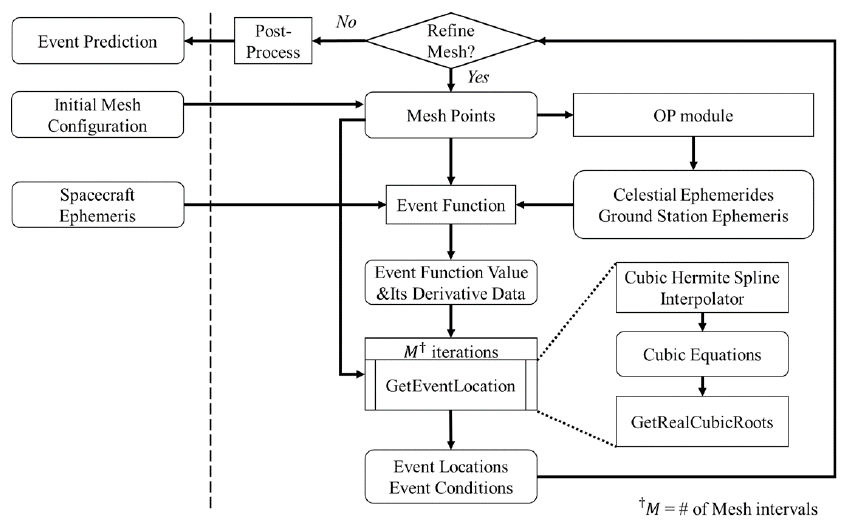
The mathematical details of the event location process are provided here. The mesh-refinement algorithm controls the outer loop of the event prediction process while the event location algorithm controls the inner loop. The mesh-refinement algorithm controls the overall quality of the event prediction solution. The event location algorithm consists of two components: the cubic Hermite spline and the analytical root-finding algorithm for cubic equations. The approach taken here has merits in that it does not require any iterative process in root-finding. The cubic Hermite spline utilizes the first derivatives, and it has a better accuracy than the (natural) cubic spline, which does not use any derivatives. An error control scheme (for instance, mesh refinement) is not applied at the event location algorithm level but at the mesh-refinement level.

The flow chart for the event prediction process is presented in Fig. 3. The user provides the spacecraft ephemeris and initial mesh configuration for the time domain. With the given mesh points, the OP module is asked to produce the ephemerides of celestial bodies and ground stations. Based on this, the event function subroutine provides event function values and its first derivatives at mesh points. For each mesh interval, the cubic Hermite spline subroutine defines a third-degree polynomial specified for the Hermite form based on event function values and its first derivatives at the end points of the interval. For each cubic function defined in an interval, the analytical root-finding subroutine for cubic polynomials analytically determines all inside roots. By repeating root-finding for all intervals, the event location is completed. The mesh-refinement algorithm increases the time sampling rate by ten times, and compares the relative errors of the roots between two different mesh configurations. The mesh-refinement algorithm continues increasing the time sampling rate until all the relative errors satisfy the user-defined tolerance or the iteration counts reaches the user-defined maximum iteration constraint. As the end product, the locations of the events and the event conditions (e.g., whether it is the beginning or end of the event) are delivered to the user as the point-type event prediction or interval-type event prediction class.

Fig. 3. Data flow chart for the event location process.

Download Original Figure

The cubic Hermite spline defines a third-degree polyno-mial in Hermite form using the function value and its first derivative at the end points of an interval (Zill et al. 2011):

$$\begin{array}{c}{\widehat{g}}_{n,n+1}\left(t\right)=a_3{\left(t-t_n\right)}^3+a_2{\left(t-t_n\right)}^2+a_1\left(t-t_n\right)+a_0\\ \left(t_n\pounds t\pounds t_{n+1}\right)\end{array}$$

(5)

where ${\widehat{g}}_{n,n+1}\left(t\right)$ is the third-degree polynomial in Hermite form and t_n is n-th mesh point. The coefficients, presented in Eq. (5), are given as follows:

$$\lceil \begin{array}{c}{a}_0\\ a_1\\ a_2\\ a_3\end{array}\rceil =\lceil \begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 1& h& h^2& h^3\\ 0& 1& 2h& 3h^2\end{array}\rceil \lceil \begin{array}{c}{g}_n\\ {\dot{g}}_n\\ g_{n+1}\\ {\dot{g}}_{n+1}\end{array}\rceil$$

(6)

where $h=t_{n+1}-t_n,g_n=g\left(t_n,X\left(t_n\right)\right)$ and ${\dot{g}}_n=\dot{g}\left(t_n,X\left(t_n\right)\right)$ . Compared to the natural cubic spline, the cubic Hermite spline generally achieves a better interpolation accuracy using the first derivatives when constructing the cubic equation in an interval. The absolute accuracy, as opposed to the relative accuracy, of the cubic Hermite spline is affected by both the event function and mesh point configuration.

Although the analytical expressions of the roots of cubic equations are elementary, they are not presented here due to their complexity. Experience using the cubic Hermite spline and analytical roots indicates that even for real roots, the analytical roots obtained in the complex space can contain numerical noise in the complex component. They seem to be affected by the cubic Hermite spline and the MATLAB built-in algorithm for calculating the cubic roots in the complex space. However, for a typical mesh interval of 60 sec, the numerical noise in the complex component is less than ${10}^{-7}\sqrt{-1}$, which is infinitesimal with respect to event prediction for real mission applications. Thus, the EP module ignores numerical noise in the complex component of less than ${10}^{-7}\sqrt{-1}$ to effectively determine the real roots.

4.3 Example: Solar Outage Prediction

This subsection evaluates event prediction capability using a solar outage (or, solar interference) prediction example. Solar outage is a phenomenon whereby radio signals from a spacecraft are obscured by solar radiation. To prevent unexpected communication problems, it is necessary to predict the timing and duration of solar outage events for the entire mission duration. Note that the explanations for the example are rather brief because the objective here is not to justify the approach taken in the EP module but to give an idea how the EP module solves event prediction problems.

Here, a solar outage prediction simulation result is presented for a lunar orbiter. The outage angle defines when the outage occurs. If the angular separation between the spacecraft and the Sun is less than the outage angle, the signals from the spacecraft are expected to be obscured by solar radiation. An empirical approximation formula for the outage angle θ_SI is adopted to predict solar outage, as follows (Vankka & Kestilä 2014):

$${\theta }_{\text{SI}}=\frac{6\sqrt{BW}}{F_{\text{D}}{D}_A}+{\theta }_{\text{Sun}}\hspace{0.17em}\hspace{0.17em}\text{in}\hspace{0.17em}\text{degree}$$

(7)

where θ_sun = 0.25° is the apparent angular radius of the Sun, BW is the antenna beam width in decibels, F_D is the downlink frequency in GHz, and D_A is the antenna diameter in meters. Note that, typically, BW~3 dB is assumed so that $6\sqrt{BW}\cong 10.4$. Using the hour angle α and the altitude angle δ measured at the ground station, an event function for the solar outage can be defined as follows:

$$g_{\text{SI}}\left(t,X\right)=\text{cos}\left({\theta }_{\text{SI}}\right)-\text{cos}\left(\Delta \alpha \right)\text{cos}\left(\Delta \delta \right)$$

(8)

where $\Delta \alpha ={\alpha }_{\odot }-{\alpha }_{\text{SC}},\hspace{0.17em}\Delta \delta ={\delta }_{\odot }-{\delta }_{\text{SC}}$, and the subscripts ⊙ and SC represent the Sun and the spacecraft, respectively. From Eq. (8), the solar outage is expected to occur wheṅ g_SI(t, X) ≤ 0. Therefore, when g_SI(t, X) = 0, the sign of ${\dot{g}}_{\text{SI}}\left(t,X\right)$ determines whether it is the beginning or end of the solar outage.

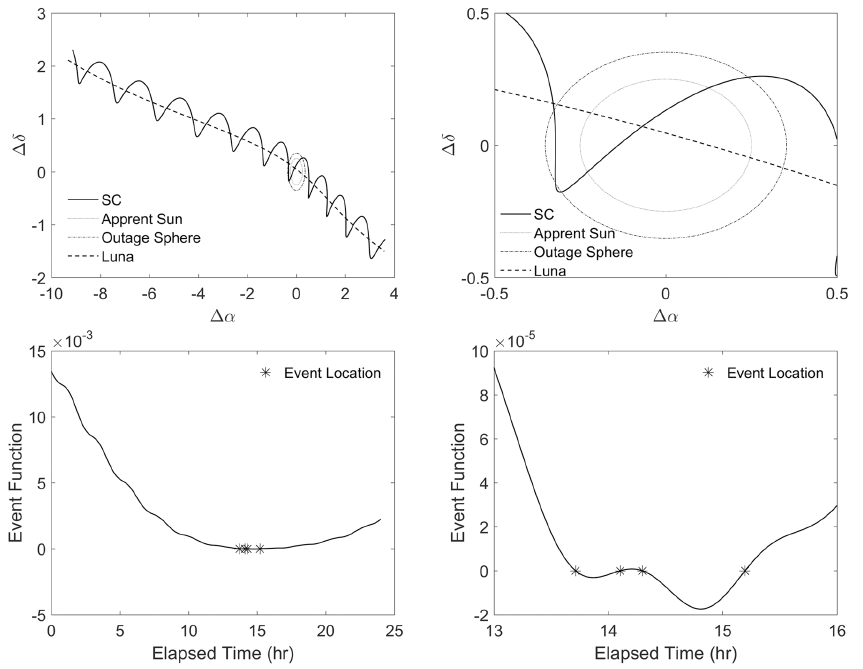
In the simulation, DSODS predicts the solar communi-cation outage of a lunar orbiter observed by a nominal Daejeon station (36.38°N, 127.35°E, altitude = 102 m). This simulation begins at TAI 01 Sep 2035 10:00:00, and ends 23 hr later. The current simulation of solar outage is based on the total lunar eclipse, which will be observable by the Daejeon station at 02 Sep 2035 because, in usual conditions, solar outages are rare for lunar orbiters, and also a lunar orbiter can experience a solar outage when a solar eclipse is observable by the ground station. In this simulation, θ_SI ≅ 0.35° is applied by setting BW = 3.4 dB, F_D = 11.95 GHz, and D_A = 9 m. The upper left and right figures in Fig. 4 present the spacecraft relative trajectory on the local celestial sphere of the Daejeon station with respect to the apparent Sun. The solar outage occurs when the spacecraft is located inside of the outage sphere. According to the figures, the solar outage occurs twice during the simulation. The lower left figure in Fig. 4 presents the solar outage event function for the entire duration, and the lower right figure in Fig. 4 presents this event function for 14-16 hr, where the solar outage occurs twice. These parts of Fig. 4 indicate that DSODS succeeded in locating all four real roots in the solar outage event function.

Fig. 4. Event prediction results: (upper left and right figures) showing the spacecraft relative trajectory on the celestial sphere on different scales, and (lower left and right figures) the event function values on difference scales.

Download Original Figure

4.4 Validation and Verification Tests

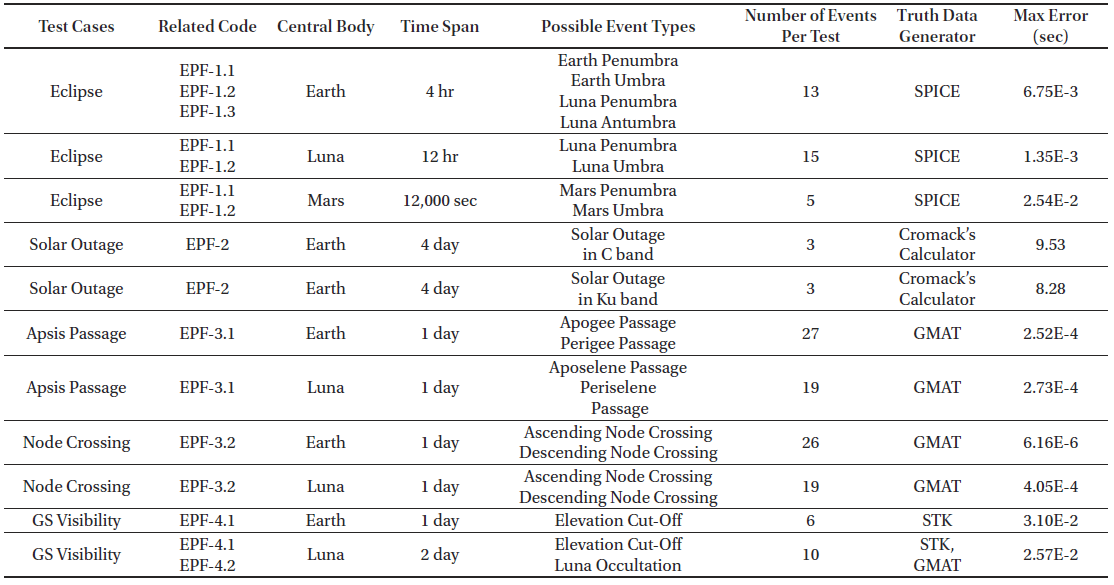
To validate and verify DSODS’s event prediction capabil-ities, eleven test cases were implemented according to the functionality requirements presented in Table 3, and corresponding test results are presented in Table 4. When DSODS was executed for event prediction under a typical desktop environment, each test case took up to a few tens of seconds. For most test cases, external truth data were provided by various sources including GMAT, STK, or SPICE, whose event prediction capabilities have been proved through a number of real mission applications. Also, for most functionality codes, there were at least two tests simulated in Earth and Luna orbits, except EPF-2, which relates to solar outage. No tests on trans-lunar orbits were included in the test cases because a trans-lunar orbit is essentially an Earth orbit in terms of its dynamic characteristics.

Table 4. Event Prediction Validation and Verification Result Summary

Download Excel Table

For the tests on EPF-1, which relates to an eclipse by an ellipsoidal body, there were three test cases simulated for Earth, Luna, and Mars because Mars is a more oblate body than Earth so a Mars orbit is a better testbed to check the effects of an ellipsoidal body. In addition, antumbra and umbra are mutually exclusive, while umbra is a more common event than antumbra. Thus, a carefully designed simulation was conducted to generate and test Luna antumbra prediction using an annular solar eclipse, which will be observed by ground observers on 26 Jan 2028 (GSFC 2017).

The test problem setting on the functionality code EPF-2 was different from the other cases in two aspects: first, only tests in Earth orbits were solved; and second, the truth data were produced by a web calculator (Cromack Industries Inc. 2017) rather than flight-proven software such as SPICE or STK. The two differences arose because solar outages regularly occur for geostationary satellites, and most analyses were focused on satellites in geostationary orbits. As a result, the test cases on EFP-2 included two tests for C and Ku bands to test the dependency on the uplink frequency (see Eqs. (5)-(6)) instead of central bodies and orbits. It is suggested that the tests on solar outage prediction were less robust than the other functionality codes. However, DSODS’s responsibility on solar outage prediction is limited to provide only an approximate geometrical estimation on solar outage rather than an accurate communication quality prediction, which requires radio engineering-based analysis on spacecraft and ground stations with a number of parameters (Vankka Kestilä 2014). Therefore, applying less robust tests for solar outage prediction can be justified by limiting DSODS’s responsibility to geometrical prediction rather than radio engineering-based communication quality prediction.

The KPLO does not yet have solid performance requirements on event prediction capabilities; therefore, the current verification results are preliminary and not confirmed. However, as shown in Table 4, most test cases showed a maximum error in the range of 10^-2 sec compared to the truth data obtained by other software packages. DSODS’s maximum error level agrees with the differences in the event predictions made by distinct software packages like STK, GMAT, and SPICE. For instance, the difference between Earth eclipse predictions made by SPICE and STK are on the sub-second level. Therefore, considering that the responsibility of the EP module is to aid the mission planning and design process, a maximum error level of 10^-2 sec is thought to be sufficient to satisfy KPLO’s event prediction capability requirements. Moreover, the event prediction results on solar outages are different from those of a web calculator by less than ten seconds. To achieve the best matches, the following parameter values are used: θ_Sun = 0.5°, BW = 2.5 dB, F_D,C-band = 4.0 GHz, and F_D,Ku-band = 12.0 GHz. Note that it is possible to reduce the differences between DSODS solar outage prediction and the external data by tuning related parameters. However, it does not seem critical because the responsibility of DSODS is to provide an approximate geometrical estimation on the occurrence of solar outages rather than an accurate link margin design and analysis.

5. SUMMARY AND CONCLUSIONS

DSODS has been developed to support the KPLO mission, and its development objective is to provide the following functionalities: orbit determination with DSN measurement models using the batch least squares estimation; DSN tracking data simulation; and event prediction to aid mission planning and design. To achieve the development objective, DSODS consists of one library and four modules: CUCL, OP, OD, DS, and EP, and uses the MATLAB object-oriented programming approach. The module-level data flow diagrams, presented in Section 2, explain how the modules interact with each other to perform orbit determination, measurement data simulation, and event prediction. To address some key concepts commonly used by all modules, the CUCL includes epoch time, coordinate system base, spacecraft, ground station base, and Hermite ephemeris classes. These classes are used in modular level interfaces, and play an important role in supporting various input and output interface specifications. Details of these classes are explained in Section 2.

To save time and effort on the development period, DSODS utilizes the GMAT as a third-party software for fundamental astrodynamics-related operations such as time and coordinate system conversions and high-fidelity orbit propagation in deep space. Although utilizing the GMAT affects the execution environment and limits the applicability of DSODS, all dependence on the GMAT is isolated in the OP module so that the GMAT can be replaced with other third-party software, if necessary.

Regarding the validation and verification of DSODS’s event prediction capabilities, eleven test cases were implemented to cover all functionality requirements. Although the KPLO does not yet have solid performance requirements, the achieved accuracy level of event prediction seems to be sufficient to support the KPLO for mission design and planning. As presented in Section 4, the event prediction results on most test cases showed a maximum error in the range of 10^-2 sec, compared to the flight-proven mission analysis software packages such as GMAT, STK, and SPICE. Moreover, sub-second level differences in event predictions can be observed between them. Less accurate event prediction results were only obtained for solar outage prediction, with errors less than 10 sec obtained due to the uncertainty of related parameters in the simulation. However, such errors in solar outage prediction are not thought critical for real mission applications because DSODS is responsible for providing an approximate geometrical estimation of the occurrence of solar outages rather than an accurate link margin design and analysis on solar interference, which requires detailed radio engineering analyses.