1 INTRODUCTION
As part of the Korean lunar exploration program (KLEP) announced in 2013 (Ju et al. 2013), the first phase of the KLEP was recently initiated; an experimental lunar pathfinder, named the Korea Pathfinder Lunar Orbiter (KPLO), will be launched in 2019. The KLEP is composed of two phases with three separate missions. The main objective of the first mission phase is to develop and demonstrate the core technologies required for the secondphase missions and for further deep space exploration missions, including establishment of the Korea deep space antenna (KDSA). After the first phase, a lunar orbiter and lander with a small rover will be launched separately in the 2020s, using the Korean space launch vehicle (KSLV)- II, which is currently in development (Ju et al. 2013). For nominal mission operation of the KPLO, an altitude of approximately 100±30 km will be maintained around the moon, with a mission duration of no longer than 12 months, including the commissioning phase. The launch mass of the KPLO is expected to be approximately 550 kg, including a scientific payload mass of approximately 40 kg (LERD 2014). A total of seven or eight scientific payloads (including payloads developed by Korea and payloads developed through international collaboration) will be loaded on board, including an imaging camera (with a resolution of less than 5 m) as the primary payload. Four 30 N thrusters will be used as the main thrusters for large burns, such as trajectory corrections during the transfer and the lunar orbit acquisition (LOA) phase. Eight 5 N thrusters will be used primarily for small burns, such as momentum dumping and orbital maintenance maneuvers during the nominal mission phase (LERD 2014).
To ensure a successful launch for the KPLO mission, the Korean aeronautical and space science community has performed numerous related mission studies and the Korea Aerospace Research Institute (KARI) has also been performing pre-phase work. Generally, there are several essential maneuvers that should be executed during each of the different lunar mission phases. First, a trans-lunar injection (TLI) maneuver should be executed to insert a spacecraft from an Earth parking orbit into a trans-lunar trajectory. Second, during the cruising phase, several midcourse corrections (MCCs) should be performed to correct errors from a TLI maneuver and to precisely aim for the target arrival point on the moon. Finally, a spacecraft will perform several lunar orbit insertion (LOI) maneuvers to be captured and orbit around the moon at the desired mission orbit altitude. Several preliminary design studies have already been conducted for the lunar mission trajectory design and analysis (Song et al. 2008, 2009, 2010; Woo et al. 2010; Song et al. 2011; Choi et al. 2013). Nevertheless, these design studies were primarily focused on generating the optimal trajectory, namely the nominal trajectory planning points of view for the maneuvers listed above. Indeed, all of these maneuvers may have associated uncertainties, such as engine burn performance, the spacecraft attitude during the maneuver, and pre-maneuver orbit uncertainties. Moreover, associated uncertainties may govern not only the entire maneuver plan but also the overall system requirements during the early design phases. Therefore, uncertainties of the pre-maneuver orbit (position and velocity), attitude, and maneuver burn performance should be considered during the early system design phase to determine and generate orbit, attitude, and thruster performance requirements for the spacecraft bus and for the flight dynamics subsystem at the ground control center.
Therefore, the focus of our work is to analyze the earlydesign- phase uncertainty requirements for orbit, attitude, and burn performance for the spacecraft itself. Thus, only the 1st LOI maneuver is considered; it is the largest burn performed utilizing an onboard propulsion system. The 1st LOI maneuver is not only the largest maneuver but is also very critical during the operation as the success of the lunar capture is directly affected by the performance achieved by this maneuver. With assumed initial uncertainty conditions in the pre-maneuver orbit (position and velocity) and the attitude and maneuver burn performances at the moment of the 1st LOI maneuver, our current work analyzed three major requirements for the early system design phases. First, the minimum requirement for the burn performance of the 1st LOI maneuver to achieve capture around the moon was estimated. Second, the requirements for orbit, attitude, and maneuver burn performance were simultaneously estimated to maintain the 1st elliptical orbit around the moon, achieved within a given orbital period. The main reason for constraining the orbital period of the captured elliptical orbit is to maintain the pre-scheduled ground station contact time. Finally, conditions regarding the dispersion characteristics of the B-plane target aiming point were also analyzed to derive the requirements for the MCC maneuver targeting accuracy during the lunar transfer phase. In Section 2, the simulation method is described in detail, including the equations of motion, accounting uncertainties, and diverse assumptions made to simulate the problem. A detailed analysis of the three major results derived from the current study is provided in Section 3, and the concluding remarks are given in Section 4. Based on the results of the current analysis, more detailed system requirements for the KPLO mission can be prepared and established, particularly for the spacecraft bus itself and for the flight dynamics subsystem at the ground control center. In addition, a contingency trajectory design plan should be developed.
2 SIMULATION SETUP
Two-body equations of motion for the spacecraft after the 1st LOI maneuver can be expressed as (Vallado 2013)(1)(2)
with the initial position, r0, and velocity, v0, vectors of the spacecraft after the 1st LOI execution (Vallado 2013).(4)
Here, μ is the gravitational constant of the moon, r and v denote the position and velocity vectors, respectively, and rhyp and vhyp denote the hyperbolic arrival position and velocity vectors of the spacecraft at the periapsis, respectively. ΔvLOI is the delta-V of the applied 1st LOI maneuver, assumed to be an impulsive burn in the current study to capture the spacecraft in orbit around the moon. As shown in Eq. (3), rhyp can be obtained directly from r0, and vhyp can be obtained as follows:
where M is a transformation matrix that converts the states expressed in the inertial frame into the radial-tangentialnormal (RTN) frame, and νrtn is the periapsis velocity vector of the hyperbolic approach trajectory with its vector components of vr, vt, and vn. And vr, vt, and vn are the radial, tangential, and normal components of the periapsis velocity vector, respectively; they can be defined as vt = vapp, and vr, vn = 0, where vapp is the magnitude of the hyperbolic approach velocity at periapsis. M can be computed using r0 and v0, and these vectors can be directly obtained using the six orbital elements (a0, e0, i0, ω0, Ω0, ν0) of the 1st capture orbit, which are all predesigned parameters. The semi-major axis, a0, of the 1st capture orbit can be computed using the desired orbital period of the 1st capture orbit, P; the eccentricity, e0, can also be derived using the mission-dependent radius of the closest approaching periapsis, rp, as shown in Eq. (6) (Brown 1998).
In Eq. (6), Rm is the mean radius of the moon, and hp is the periapsis altitude at the moment of closest lunar approach, which is also a pre-defined value. Other elements such as inclination, i0, argument of periapsis, ω0, right ascension of ascending node, Ω0, and true anomaly, ν0, are missiondependent parameters that are determined during mission definition or during the LOA phase design. The definitions shown in Eqs. (3)-(5) are valid as the current study assumed that the 1st LOI maneuver was executed at the periapsis with an impulsive maneuver.
To consider uncertainties in the initial conditions of the 1st LOI maneuver (pre-maneuver uncertainty for both position and velocity) and maneuver performance during execution (attitude and burn magnitude), statistical dispersion analysis was performed using Monte Carlo simulations. The perturbed initial position, , and velocity, , of the spacecraft at the moment of the 1st LOI maneuver execution are constructed as follows:
Here, randn(0,1) is a Gaussian random number generator with zero mean and a unit standard deviation (Ross 2009); are the expected pre-maneuver position (indicated by superscript pos) and velocity (indicated by superscript vel) uncertainties. is the perturbed 1st LOI maneuver with both three-dimensional attitude and burn magnitude uncertainties and can be modeled as
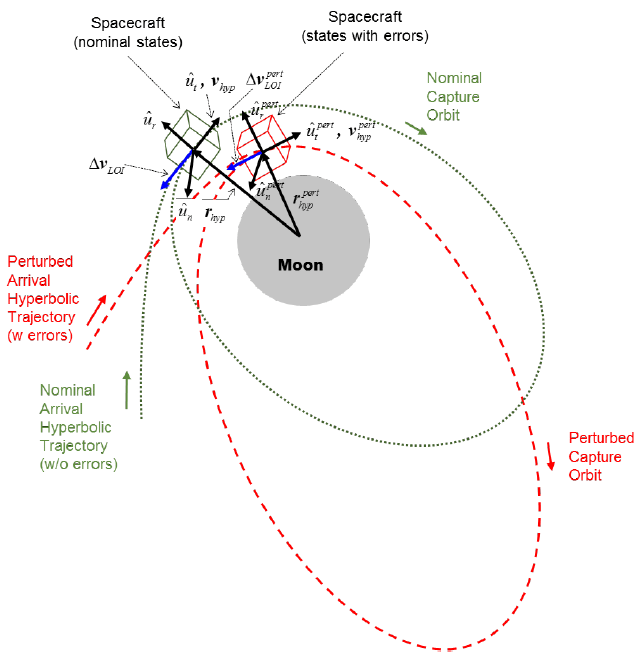
where ΔvLOI is the magnitude of the nominally planned 1st LOI maneuver, σdvm is the expected magnitude error of that maneuver, Q is a 3-by-3 transformation matrix to reflect the three-dimensional attitude uncertainty as a function of the expected errors in the radial () , transverse (), and normal () directions. Again, M is a transformation matrix that converts states expressed in the inertial frame into the RTN frame; finally, is the unit vector of the perturbed states expressed in the RTN frame, which can easily be determined from the initial states of and . In Fig. 1, the exaggerated geometry of the 1st LOI maneuver, nominal vs. the case with an initial error condition, is shown. Using the initial perturbed states shown in Eqs. (7a) and (7b), the 1st capture orbit is numerically propagated using the Runge– Kutta–Fehlberg 7–8th order variable step size integrator. In addition, the uncertainties in the apoapsis and periapsis approach conditions of the 1st lunar capture orbit (due to the perturbed initial conditions) are determined using the root-finding algorithm described in Brent (2002) with implementation of the proper objective functions.
As the current study focused on an early design phase uncertainty analysis, two-body equations of motion are used, and the 1st LOI burn is assumed to be an impulsive maneuver. Furthermore, the direction of the 1st LOI maneuver is assumed to always be in the direction opposite to the velocity vector at the periapsis of the orbit. The spacecraft is assumed to have already approached the periapsis with a hyperbolic arrival trajectory around the moon, and the orbital element of the 1st target capture orbit is assumed to be i0 = 90°, with values of 0° for ω0, Ω0 and ν0. The other orbital elements, a0 and e0, are determined from the pre-defined values of vapp, P, and hp. The current study assumed vapp to be within the range of 2.4–2.6 km/s, hp is assumed to be 100, 200, and 500 km, and P is assumed to be 12 or 24 hr, considering the human factors that may be a major consideration while establishing operation schedules.
3 SIMULATION RESULTS
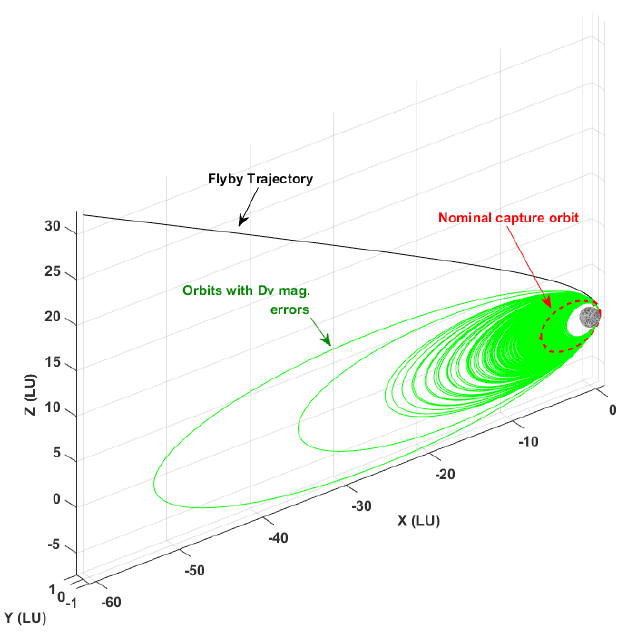
First, the minimum maneuver burn performance requirement to achieve capture around the moon was investigated. As the current study assumed an impulsive maneuver, the maneuver burn performance can simply be regarded as the magnitude of the executed maneuver. Among the various error sources described in Subsection 2.2, only σdvm was considered for the current simulation, while the other errors were set to zero. For σdvm, it was assumed that a maximum of 0–80 % of the error (3σ) occurs with respect to the magnitude of the nominally planned delta-V maneuver; given that error is increased in 5 % steps during the simulation, a total of 1,000 Monte Carlo runs were performed for the statistical analysis. The main purpose of this simulation is to evaluate the sensitivities of the maneuver burn performance that directly affect the shape of the 1st capture orbit. Through this analysis, the minimum burn requirement to achieve capture around the moon can be estimated, which may aid in establishing additional plans for contingency trajectory options during the early system design phase. Tables 1 and 2 show the maximum allowable maneuver magnitude errors for cases in which the 1st elliptical capture orbits have an orbital period of 12 hr (Table 1) or 24 hr (Table 2). If the maneuver magnitude errors are greater than those shown in Tables 1 and 2, the spacecraft is not captured, and it will fly past the moon. As expected, Tables 1 and 2 clearly show that the maximum allowable maneuver magnitude errors decrease with an increase in the assumed magnitude of the hyperbolic arrival velocity, at periapsis, with its altitude. For example, if the spacecraft is targeted to approach the moon with a periapsis arrival velocity of 2.4 km/s at a 100 km altitude, and if a 12 hr orbital period is desired for the 1st capture orbit, then the spacecraft can still be captured around the moon, even if maneuver magnitude errors reach approximately 65 %. If the hyperbolic arrival velocity at periapsis is increased to approximately 2.5 km/s, the maximum allowable maneuver magnitude errors decrease to approximately 50 %. Although the spacecraft can still be captured in orbit around the moon in both cases, the resultant shape of the captured orbit due to the maneuver burn errors should be carefully considered. For example, a resultant capture orbit could have a minimum and maximum apoapsis altitude of approximately 2,324 km and 501,628 km, respectively, (approximately 65 % of the maneuver burn error case) and a minimum and maximum apoapsis altitude of approximately 2,386 km and 264,667 km, respectively, (approximately 50 % of the maneuver burn error case). In Fig. 2, the resultant capture orbits with a maneuver burn magnitude error of approximately 70 % (targeted to approach the moon with a periapsis arrival velocity of 2.4 km/s at a 100 km altitude) are shown for the case in which the orbital period of the nominal capture orbit is assumed to be 12 hr. Fig. 2 clearly shows that there exists a perturbed trajectory not captured by the moon owing to the maneuver burn magnitude error; even if captured, the apoapsis altitude of the same orbit appears to reach approximately 50 LU (1 Lunar Unit = approximately 1,738.2 km). These results indicate that even if capture around the moon is achieved, the orbit could have an extremely high apoapsis altitude (even more than the Earth-moon distance), which decreases the suitability of the derived maximum allowable errors for the maneuver burn performance. Considering diverse combinations of periapsis arrival velocity, target periapsis altitude, and desired orbital period for the 1st capture orbit, we can conclude that the 1st LOI maneuver should be executed within errors less than approximately 25 % of the magnitude with respect to the nominally planned delta-Vs, as clearly shown in Tables 1 and 2. This result indicates that it is still possible to achieve capture around the moon in the case where one of the four main onboard engines malfunctions during the LOA phase. This is the current baseline design of the KPLO propulsion system. Similar analysis results can be found in studies performed by Houghton et al. (2007), which reported that an error of less than approximately 50 % in the nominally planned delta-V is required for a successful LOI maneuver and that larger maneuver errors must be avoided as they weakly capture or fly by the moon. Based on the currently estimated minimum burn performance analysis, the early LOA phase design strategy can be further improved, including a contingency trajectory design plan.
In this subsection, the effect of the combined uncertainties (including orbit, attitude, and maneuver burn performance) at the moment of the 1st LOI maneuver execution on the characteristics of the 1st capture orbit is analyzed. For the initial error conditions, σpos and σvel are given within a range of 0–10 km and 0–10 m/s (increased in 2 km and 2 m/s steps, respectively) with respect to its nominal position and velocity, σdvm is given within a range of 0–10 % (increased in 1° steps) with respect to its nominally planned delta-V maneuver magnitude, and finally, σatt is given within a range of 0–10° with a 2° step, respectively. Note that these uncertainties are all in three-sigma and given under conditions related to the worst cases of the KPLO system design configuration and with adequate margin. With the assumed initial condition uncertainties, 1,000 Monte Carlo runs were performed for the statistical analysis. For the orbital period constraints of the 1st capture orbit, a maximum difference of 1 hr is assumed to be allowed with respect to the nominally planned 12 or 24 hr for the current study as the orbital period with regard to the pre-scheduled ground station contact time. In Tables 3 and 4, the maximum allowable delta-V magnitude errors are shown with respect to the orbit (position and velocity) and attitude errors to meet the given constraints of a 1 hr orbital period difference for the nominally planned 12 hr (Table 3) or 24 hr (Table 4) of the orbital period of the 1st capture orbit. In Tables 3 and 4, the allowable delta-V magnitude errors are shown as percentage values with respect to the nominal delta-V magnitude; the magnitude of the hyperbolic arrival velocity at periapsis is assumed to be 2.4 km/s for this simulation. A status of “Not Available” in both tables indicates that the orbital period of the 1st capture obit cannot be achieved within 1 hr from the nominally planned orbital period, due to uncertainties posed upon the position, velocity, and attitude at the moment of the 1st LOI maneuver, even if the maneuver burn is performed perfectly. As expected, Tables 3 and 4 clearly show that smaller errors in the delta-V magnitude are required if the 1st capture elliptical orbit is intended to remain within a period of 24±1 hr rather than 12±1 hr; this phenomenon originates from the orbit periapsis velocity characteristics. Regardless of the periapsis altitude, we can conclude from Table 3 that the delta-V burn should be executed with an error of approximately 2 % or less, with position errors of less than approximately 4 km, velocity errors of approximately 4 m/s, and attitude errors of approximately 8° to maintain the orbital period of the 1st capture orbit within 12±1 hr. However, if the periapsis altitude is fixed at 100 km, the maximum allowable delta-V magnitude error is increased to 4 % for the same attitude, with position and velocity errors of approximately 2 km and 2 m/s, respectively.
Unlike the cases shown in Table 3, the maximum allowable delta-V magnitude errors and the position, velocity, and attitude errors are greatly reduced if the spacecraft is intended to be captured around the moon with an orbital period of 24±1 hr. We can conclude from Table 4 that the delta-V burn should be executed to have approximately 1 % error, with position errors of less than approximately 2 km, velocity errors of approximately 2 m/s, and attitude errors of approximately 6° to limit the orbital period of the 1st capture orbit to within 24±1 hr. Moreover, the allowable periapsis altitude for this case is only 100 km, and the spacecraft cannot be captured within 24±1 hr of elliptical orbit at a higher periapsis altitude, even with smaller initial errors. From the findings discussed above, the following factors are reemphasized and confirmed: the importance of considering diverse errors during the early design phase of LOA, allocating proper system requirements in the orbit, attitude, and onboard propulsion system, and considering human factors regarding the operation schedule. LOI burns in the real world may be executed with a finite burn, and associated results may differ from the results in the current study. However, a more detailed and profound analysis can be further conducted using the current results as a baseline.
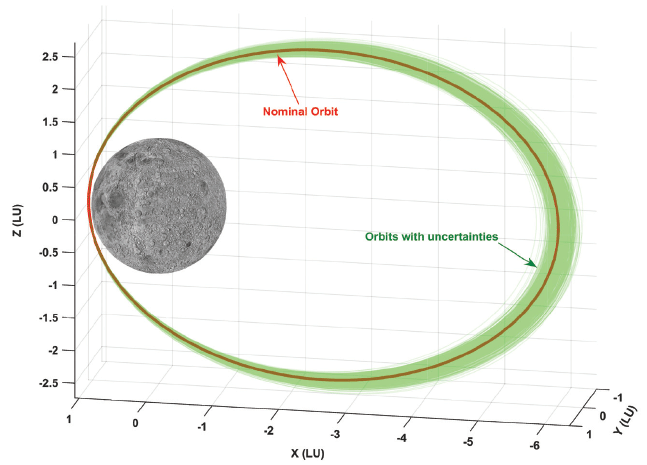
Owing to the initial error conditions, the resultant capture orbit will have a perturbed shape. In Fig. 3, an example of a perturbed capture orbit is compared to the nominal orbit. Again, each of the axes in Fig. 3 is scaled to LUs. In this plot, a 12 hr 1st capture orbit with a 100-km periapsis altitude is assumed with initial error conditions of 6 km (3σ) and 6 m/s (3σ) for position and velocity error, respectively, 10° (3σ) of attitude error, and 2 % (3σ) of delta-V magnitude error, at the moment of the LOI burn execution. In Table 5, the resultant orbital characteristics of the perturbed 1st capture orbit are shown. The semi-major axis of the captured orbit is significantly affected (approximately 6,178±99 km) because of the diverse initial error conditions. Thus, the apoapsis altitude is approximately 8,779±198 km. This result is primarily caused by errors in the delta-V magnitude, which is only approximately 2 % from the nominal value.
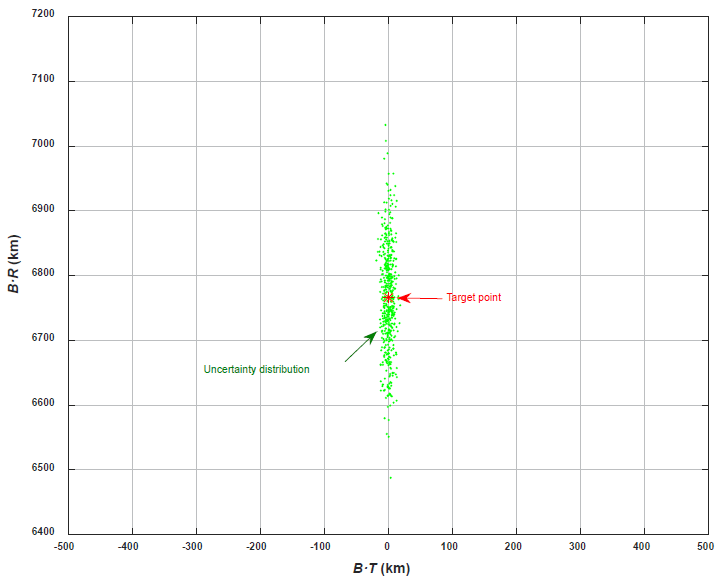
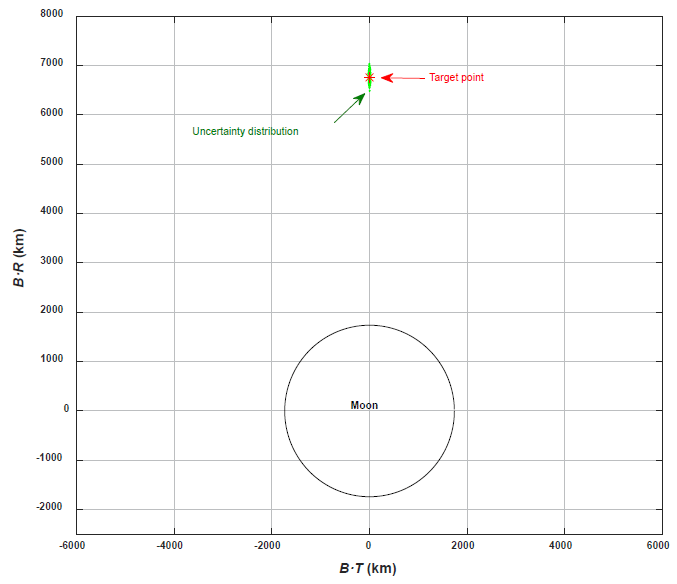
In planetary missions, one of the most challenging problems is to design a transfer trajectory that takes the spacecraft within a very close vicinity of the target planet. One possible approach for placing the spacecraft close to a target planet is the B-plane, or body plane, targeting method. B-plane targeting can be achieved by performing an MCC during the transfer phase, and then an orbit insertion maneuver can be performed to achieve capture into the orbit of the target planet. To aim the target point, the B-plane coordinate system is used, which can be thought of as a target frame attached to the aiming central body. The B-plane is defined as a plane passing through the center of a target body normal to the incoming asymptote vector of the approach hyperbola; this plane is often described by its two components, B·T and B·R. Here, B is the vector that points to the aiming points, and T and R are the defined unit axes from the orthogonal set to the incoming asymptote vector of the approach hyperbola (Sergeyevsky et al. 1983). Details on the B-plane system are omitted in the current study as the B-plane system is not the main concern of the current work. However, more details on the definition and usage of the B-plane coordinate frame can be found in Kizner (1961), Sergeyevsky et al. (1983), and Jah (2002). Using the initial error conditions of position and velocity at the moment of the 1st LOI maneuver discussed above, the characteristics of the error distributions on the B-plane coordinate system can easily be analyzed. Therefore, the required targeting accuracy during the lunar transfer phase can be determined. In Fig. 4, the allowable B-plane targeting errors (uncertainty distribution) for a selected lunar capture condition are shown, and Fig. 5 presents a magnified view of Fig. 4. To plot the uncertainty distribution on the B-plane coordinate system shown in Figs. 4 and 5, the periapsis altitude of the 1st capture orbit is assumed to be 100 km with an orbital period of 12 hr. The initial error conditions assumed at the moment of the LOI burn execution are described as follows: 6 km (3σ) and 6 m/s (3σ) for the position and velocity error, respectively, 10° (3σ) for the attitude error, and 2 % (3σ) for the delta-V magnitude error. With the assumed initial position and velocity errors, distributions of the allowable B-plane targeting errors can easily be derived and used as reference values during the trans-lunar phase operation to determine whether additional error cleanup MCCs are required. These dispersions shown in Figs. 4 and 5 can be regarded as B-plane entry corridor conditions for successful capture around the moon, under given position, velocity, attitude, and delta-V magnitude errors at the moment of the LOI burn execution. In Table 6, the dispersion characteristics shown in Figs. 4 and 5 are summarized. From Table 6, we can conclude that MCC maneuvers during the lunar transfer should target the B-plane within approximately 0.184±6.349 km for B·T and approximately 6,794.914±80.799 km for B·R. Generally speaking, B·T errors may represent errors out of the desired orbit plane about the moon, and B·R errors represent errors in arrival altitudes. If these error conditions are measured as a two-dimensional distance from the aiming point, then the allowable mean error distance from the aiming point will be approximately 65.105±48.194 km. The resulting acceptable error ranges for target aiming points on the B-plane frame are consistent with those used for the Chandrayaan program, which is managed by the Indian Space Research Organisation (ISRO). The errors for this program were approximately several tens of km from the reference target center point on the B-plane coordinate frame (Pitchaimani 2015, private communication).
| Parameter | Nominal | Mean | Standard deviation |
|---|---|---|---|
| B dot T (km) | 0.000 | 0.184 | 6.349 |
| B dot R (km) | 6,765.911 | 6,764.914 | 80.799 |
| 2D distance from target center (km) | 0.000 | 65.105 | 48.194 |
4 CONCLUSIONS
As a part of an early system design and analysis for the KPLO mission, the uncertainty requirements for the orbit, attitude, and burn performance of the 1st LOI maneuver execution were estimated and analyzed. In the early system design phase, it is essential to reflect the effect of those errors as the success of the lunar capture is directly affected by the performance achieved in the 1st LOI maneuver. The current analysis assumes an impulsive LOI maneuver, and two-body equations of motion were adapted to simplify the problem for preliminary analysis. Monte Carlo simulations were performed for the statistical analysis to analyze diverse uncertainties that may arise at the moment of the maneuver execution. The spacecraft is assumed to have already approached the periapsis with a hyperbolic arrival trajectory around the moon; diverse arrival conditions or mission constraints, such as varying periapsis altitudes or orbital periods of the capture orbit after execution of the 1st LOI maneuver, were considered. As a result, three major requirements were analyzed and estimated for the early design phase of the spacecraft and for the flight dynamics subsystem at the ground control center. Regarding the minimum requirement for the burn performance needed to achieve capture around the moon, we can conclude that the 1st LOI maneuver should be executed with an error of less than approximately 25 % of the magnitude, with respect to the nominally planned delta-Vs to avoid weak capture or flying by the moon. This limit must not be exceeded, regardless of the hyperbolic approach velocity or periapsis altitude. For the requirements of orbit, attitude, and maneuver burn performance uncertainties needed to hold the 1st lunar elliptical orbit within a specified orbital period (within 1 hr for the current simulation), we discovered that tighter error conditions on position, velocity, attitude, and delta-V magnitude uncertainties were required. These restrictive conditions allowed for a longer pre-defined target orbital period and a higher target approach periapsis altitude. Finally, for the dispersion requirements on the B-plane aiming target points to meet the target insertion goal, we estimate that a distance of up to approximately several tens of km from the center point of the reference target on the B-plane frame will lead to a successful insertion into the lunar capture orbit. The importance of considering diverse uncertainties during the early design phase of the LOA and allocating proper system requirements in the orbit, attitude, and onboard propulsion system with human factors regarding the operation schedule is reemphasized and confirmed through this work. LOI burns in the real world may be executed with a finite burn type, and the associated results may differ from the results in the current study. However, more detailed system requirements on the KPLO mission are expected, particularly for the spacecraft bus itself and for the flight dynamics subsystem at the ground control center. These requirements can be further analyzed and developed based on the current results, including a contingency trajectory design plan.